Необходимость введения нового базисного переменного со значением >0 приводит к построению так называемого цикла транспортной таблицы. В табл. 10 цикл представлен направленными звеньями замкнутой ломаной
, начало и конец которой находятся в клетке, соответствующей вводимому в базис переменному модели x12. Такой цикл транспортной таблицы существует и определяется однозначно для любого переменного, вводимого в базис.
В общем случае цикл транспортной таблицы, представляемый в виде замкнутой ломаной, может иметь сложную ступенчатую конфигурацию с самопересечениями (эти самопересечения не могут быть в клетках базисных переменных). Для нас цикл транспортной таблицы интересен лишь в одном отношении: он позволяет определять те базисные переменные, из которых мы вычитаем w. Выбрав из этих переменных то, которое имеет наименьшее значение, мы получим выводимое из базиса переменное.
Задача 4. Вернемся к рассмотрению классической транспортной задачи, начатому в задачах 2, 3.
Новое допустимое базисное решение характеризуется значениями x11=2, x12=4, x22 = 1, x31=5, x33=3, x34=2 базисных переменных модели и значением целевой функции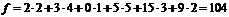 
. На этом первая итерация симплексного метода завершена.
На второй итерации система линейных алгебраических уравнений (5) для нахождения симплекс-множителей имеет следующий вид:
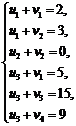
а ее решением являются значения
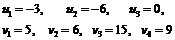
Используя полученные значения симплекс-множителей и известные удельные стоимости cij вычисляем коэффициенты для небазисных переменных согласно (6):
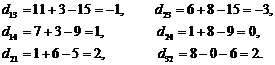
В новое допустимое базисное решение целесообразно ввести свободное переменное x23, так как |d23|=max{|d13|, |d23|, |d24|}. Для определения базисного переменного, которое необходимо вывести из базиса, воспользуемся циклом транспортной таблицы 
(табл. 11). Сравнив базисные переменные, из которых вычитается w, находим наименьшее из них: x22=1-w. Таким образом, w=1, переменное x22 должно быть выведено из базиса, а новое допустимое базисное решение характеризуется значениями базисных переменных x11=1, x12=5, x23=1,
x3l=6, x33=2, x34=2 и значением целевой функции
.
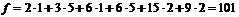Вторая итерация симплексного метода завершена.
Таблица 11
Источ- ник | Сток | Поставки | |||
1 | 2 | 3 | 4 | ||
1 2 3 | 2- 5+ | 4+ 1- |
3- | 6 1 10 | |
Спрос | 7 | 5 | 3 | 2 |
На третьей итерации система линейных алгебраических уравнений (5)для нахождения симплекс-множителей имеет следующий
вид :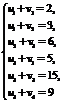 
Из этой системы находим
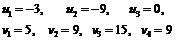
Используя полученные значения симплекс-множителей и известные удельные стоимости сij, вычисляем коэффициенты для свободных переменных согласно (6):
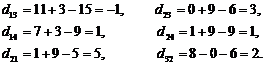
На третьей итерации отрицательную оценку имеет единственное свободное переменное x13, которое и вводим в базис. Для определения базисного переменного, которое необходимо вывести из базиса, воспользуемся циклом транспортной таблицы 
представленным в табл. 12. Сравнив базисные переменные, из которых вычитается w, находим наименьшее из них: x11=1-w. Таким образом, w=1, переменное x11 должно быть выведено из базиса, а новое допустимое базисное решение характеризуется значениями базисных переменных x12=5, x13=1, x23=1, x31=7, x33=1, x34 =2 и значением целевой функции 
.
Таблица 12
Источник | Сток | Поставки | |||
1 | 2 | 3 | 4 | ||
1 2 3 | 1- 6+ |
2- | 6 1 10 | ||
Спрос | 7 | 5 | 3 | 2 |
На этом третья итерация симплексного метода завершена. На четвертой итерации система линейных алгебраических уравнений (5) для нахождения симплекс-множителей имеет следующий вид:
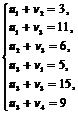
Из нее находим
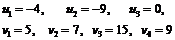
Используя полученные значения симплекс-множителей и известные удельные стоимости сij, вычисляем коэффициенты для небазисных переменных согласно (6):
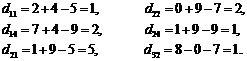
А так как все найденные коэффициенты неотрицательны, то решение рассматриваемой задачи завершено и оптимальным является допустимое базисное решение, полученное на предыдущей (третьей) итерации симплексного метода.
Если транспортная задача открыта, то она сводится к закрытой введением ложного поставщика или потребителя, которому присваивается разностная мощность, а стоимости перевозки единицы груза приравниваются 0.
МОДЕЛИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Во многих экономических моделях ИО зависимости между постоянными и переменными факторами лишь в первом приближении можно считать линейными, более детальное рассмотрение позволяет обнаружить нелинейность. Как правило, такие показатели, как прибыль, себестоимость, капитальные затраты на производство и др., в действительности зависят от объема производства, расхода ресурсов и т. п. нелинейно. В этом случае возникает задача нелинейного программирования.
Можно выделить класс нелинейных задач, которые относятся к классическим методам оптимизации. Допустим, что среди ограничений 
, нет неравенств, не обязательны условия неотрицательности, переменные не являются дискретными, m<n; а функции непрерывны и имеют частные производные, по крайней мере, 2-го порядка. В этом случае задачу оптимизации можно сформулировать так: найти переменные x1, x2,…,xn, удовлетворяющие системе уравнений
(1)
и обращающие в максимум (минимум) целевую функцию
. (2)
Такие задачи, по крайней мере, можно решать классическими методами дифференциального исчисления. Однако на этом пути встречаются такие вычислительные трудности, которые делают необходимым поиск других методов решения. Поэтому классические методы часто используются не в качестве вычислительного средства, а как основа для теоретического анализа.
Примером типичной и простой нелинейной задачи является следующая: данное предприятие для производства какого-то продукта расходует два средства в количестве x1 и x2 соответственно. Это – факторы производства, например, машины и труд, два различных вида сырья и т. п., а величины x1 и x2 – затраты факторов производства. Факторы производства впредь будем считать взаимозаменяемыми. Если это «труд» и «машины», то можно применять такие методы производства, при которых величина затрат машин в сопоставлении с величиной затрат труда оказывается больше или меньше (производство более или менее трудоемким). В сельском хозяйстве взаимозаменяемыми факторами могут быть посевные площади или минеральные удобрения (экстенсивный метод производства).
Объем производства (выраженный в натуральных или стоимостных единицах) является функцией затрат производства, 
.
Эта зависимость называется производственной функцией. Издержки 
зависят от расхода обоих факторов (x1 и x2) и от цен факторов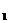 (c
и c
). Совокупные издержки выражаются формулой 
.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Основные порталы (построено редакторами)