Требуется составить оптимальный план перевозок, обеспечивающий минимальные транспортные затраты.
2. Предлагается 5 инвестиционных проектов, тщательная экономическая экспертиза которых позволяет получить для каждого из проектов достаточно убедительные экономические оценки ожидаемого эффекта от их реализации 80; 50; 75; 40; 45 усл. ед. и необходимых капиталовложений 110; 60; 80; 15; 30 усл. ед. Общий объем возможных инвестиций ограничен величиной 200 усл. ед. Необходимо так распорядиться имеющимися финансовыми ресурсами, чтобы максимизировать суммарный эффект от инвестиций.
3. Задача о рациональном раскрое строительных материалов. Часть заемных оборотных средств предприятия иммобилизована в запасы пиломатериалов: на складе имеется партия бруса, содержащая 300 штук длиной 7,5 м каждый и партия бруса, содержащая 500 штук длиной 5 м каждый. Из этого материала можно изготовить оконные блоки, в каждый из которых входит две детали по 2,5 м и три детали длиной 2 м каждая. Как оптимально использовать заемные средства, если предположить, что спрос на оконные рамы неограничен?
ТРАНСПОРТНАЯ ЗАДАЧА
Ниже приводятся примеры специальных ЗЛП – транспортной задачи и задачи о назначениях, которая интерпретируется как частный случай транспортной задачи. Задача о назначениях рассматривается, как пример задачи дискретной оптимизации.
Примеры задач транспортного типа
Задача. Перед менеджером нефтяной компании «Магнум» стоит задача создания схемы поставки нефтепродуктов от четырех нефтеперерабатывающих комплексов компании к пяти регионам страны. Одним из основных условий поставленной задачи является минимизация стоимости перевозок, при этом все мощности нефтеперерабатывающих комплексов должны бьть реализованы и все потребности регионов должны быть удовлетворены.
Мощности поставщиков и мощности потребителей, а также стоимость перевозок нефтепродуктов представлены в следующей таблице (в условных единицах).
Мощности поставщиков | Мощности потребителей | ||||
600 | 400 | 700 | 500 | 1000 | |
700 | 4 | 8 | 5 | 1 | 6 |
800 | 3 | 5 | 2 | 3 | 4 |
900 | 2 | 6 | 5 | 4 | 3 |
800 | 1 | 4 | 3 | 5 | 3 |
Решение.
В данном случае мощности поставщиков нефтепродуктов и потребности регионов в них совпадают, т. е. имеем дело с закрытой моделью транспортной задачи.
Ввод условий задачи состоит из следующих основных этапов.
1. Создание формы для решения задачи.
2. Ввод граничных условий.
3. Ввод исходных данных.
4. Назначение целевой функции.
5. Ввод зависимостей из математической модели.
6. Ввод ограничений.
7. Просмотр результатов и печать отчета.
Рассмотрим более подробно каждый из этих этапов.
1. Создание формы для решения задачи предполагает создание матрицы перевозок. Для этого необходимо выполнить резервирование изменяемых ячеек: в блок ячеек ВЗ:F6 заполняется значением 1. Таким образом, резервируется место, где после решения задачи будет находиться распределение поставок, обеспечивающее минимальные затраты на перевозку груза (нефтепродуктов).
2. Ввод граничных условий.
Введение условия реализации мощностей поставщиков, т. е.
![]()
где ai – мощность i-го поставщика;
xi, j – объем поставки груза от i-го поставщика к j-му потребителю;
п – количество потребителей.
Для этого необходимо выполнить следующие операции:
· курсор в ячейку АЗ;
· кнопка Автосумма;
· выделить необходимые для суммирования ячейки ВЗ:FЗ;
· нажать ENTER – подтверждение ввода формулы для суммирования.
Аналогичные действия выполнить для ячеек А4, А5, А6, т. е. ввести условия реализации мощностей всех поставщиков (для всех строк). Эти действия можно реализовать иначе:
· курсор в АЗ;
· кнопка Копировать;
· выделить ячейки А4:А6;
· кнопка Вставить.
Введение условия удовлетворения запросов потребителей, т. е.
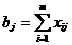
где bj – мощность j-го потребителя;
т – количество поставщиков.
Для этого необходимо выполнить следующие операции:
· курсор в В7;
· кнопка Автосумма. При этом автоматически выделятся весь столбец ВЗ:В6;
· ЕNTER – подтверждение суммирования показателей выделенного столбца.
Последовательность этих действий выполнить для ячеек С7:F7, или же:
· курсор в В7;
· кнопка Копировать;
· выделить С7:F7;
· кнопка Вставить.
Таким образом, введены ограничения для всех поставщиков и всех потребителей.
3. Ввод исходных данных.
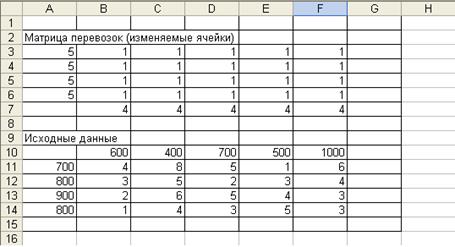
В конкретном примере осуществляется ввод мощностей четырех нефтеперерабатывающих предприятий (ячейки А11:А14), потребности регионов в их продукции (В10:F10), а также удельные затраты по доставке нефтепродуктов от конкретного поставщика потребителю (блок В11:F14).
4. Назначение целевой функции.
Для вычисления значения целевой функции, соответствующей минимальным суммарным затратам на доставку груза, необходимо в определенную ячейку ввести формулу для ее вычисления:
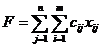
где cij – стоимость доставки единицы груза от i-го поставщика к j-му потребителю;
хij - объем поставки груза от i-го поставщика к j-му потребителю.
Для этого:
· курсор в ячейку В15. В данную ячейку будет помещаться значение целевой функции после решения задачи;
· кнопка Мастер функций;
На экране появится диалоговое окно Мастер функции шаг - 1 из 2
· выбрать категорию Математические;
· выбрать функцию СУММПРОИЗВ;
В задаче целевая функция представляет собой произведение удельных затрат на доставку груза (расположенных в блоке ячеек В11:F14) и объемов поставок для каждого потребителя (содержимое ячеек ВЗ:F6). Для этого:
· в строку Массив 1 ввести В11:F14;
· в строку Массив 2 ввести ВЗ:F6;
· кнопка ОК.
В поле ячейки В15 появится некоторое числовое значение, равное произведению единичных поставок на удельные коэффициенты затрат по доставке грузов (число 77 в данной задаче).
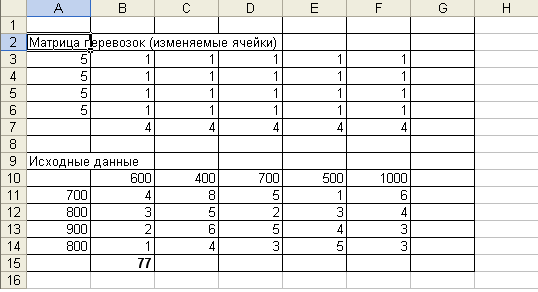
5. Ввод зависимостей из математической модели:
· выбрать Сервис ® Поиск решения;
· курсор в Установить целевую ячейку;
· ввести (выбрать) адрес $В$15.
Таким образом, производится указание ячейки, куда при решении задачи помещается значение целевой функции.
Или:
· поставить курсор в В15
· выбрать Сервис ® Поиск решения.
При этом осуществится автоматический ввод адреса $В$15 в поле адреса целевой ячейки;
· установить направление изменения целевой функции: минимальному значению.
Ввести адреса изменяемых ячеек ВЗ:F6. Для этого:
· щелкнуть в поле Изменяя ячейки;
· ввести адреса $В$3:$F$6 (или укажем на листе).
Ввести ограничение задачи. В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие реализации мощностей всех поставщиков. Для этого:
· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;
· в строке Ссылка на ячейку введем адреса (или укажем на листе) $А$3:$А$6;
· выберем знак ограничения =;
· в строке Ограничение введем адреса (или укажем на листе) $А$11:$А$14;
· кнопка OK
На экране появится диалоговое окно Поиск решения с введённым условием.
Далее вводится ограничение, которое реализует условие удовлетворения мощностей всех потребителей. Для этого:
· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;
· в строке Ссылка на ячейку введем адреса (или укажем на листе) $В$7:$F$7;
· выберем знак ограничения =;
· в строке Ограничение введем адреса (или укажем на листе) $В$10:$F$10;
· кнопка OK
6. Ввод ограничений.
Далее необходимо установить ограничения на решение задачи. Для этого:
· кнопка Параметры.
· на экране диалоговое окно Параметры поиска решения:
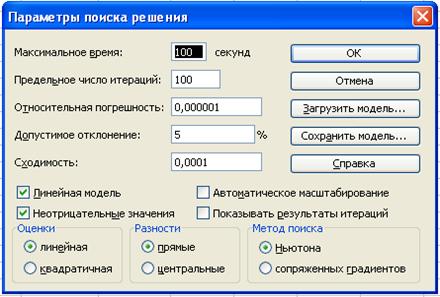
· установим флажки:
ü Линейная модель (это обеспечит применение симплекс-метода)
ü Неотрицательные значения, так как объемы поставок груза отрицательной величиной быть не могут;;
· кнопка ОК.
· на экране появится диалоговое окно Поиск решения;
· кнопка Выполнить.
7. Просмотр результатов и печать отчета. После выполнения всех вышеуказанных действий на экран выводится окно Результаты поиска решения
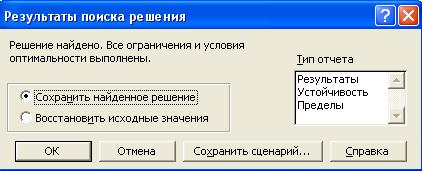
· В окне Тип отчета выбрать интересующий вид отчета.
· кнопка ОК.
Внизу страницы экрана содержится сообщение Отчет по результатам 1. Щелкнуть на этом сообщении, на экран выводятся результаты решения задачи, которые можно распечатать.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
 Основные порталы (построено редакторами)
Основные порталы (построено редакторами)

