Имеем три стационарные точки: X
(0;0), X
(1;1), X
(-1;-1).
Найдем вторые частные производные, используя (6):
;
;
;
.
Вычисляем значения вторых частных производных в каждой стационарной точке, составляем определитель D и применяем достаточные условия экстремума.
В точке X(0;0) a
=-2; a
=a
=-2; a
=-2.
.
Вопрос об экстремуме остается открытым (такая точка называется седловой).
В точке X2(1;1) (а также и в X3 (-1;-1)):
Функция в этих точках имеет минимум, так как
.
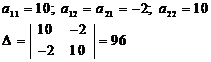
Выше речь шла о локальном экстремуме функции n переменных. Как правило, в практических задачах необходимо определить наименьшее и наибольшее значения функции (глобальный экстремум) в некоторой области.
Говорят, что функция 
имеет в точке 
заданной области D глобальный максимум (наибольшее значение) или глобальный минимум (наименьшее значение), если неравенство 
или 
, соответственно выполняется для любой точки XÎD.
Если область D замкнута и ограничена, то дифференцируемая функция достигает в этой области своих наибольшего и наименьшего значений или в стационарной точке, или в граничной точке (теорема Вейерштрасса).
Следовательно, чтобы найти наибольшее (наименьшее) значение функции в области D, нужно:
1) найти все стационарные точки внутри области D и вычислить значения функции в них;
2) исследовать функцию на экстремум на границе области;
3) сравнить значения функции, полученные п. 1) и 2): наибольшее (наименьшее) из этих чисел и будет наибольшим (наименьшим) значением функции во всей области.
Граница области D аналитически может быть задана системой уравнений (условий) относительно переменных x
, x
, …, x
. Поэтому, исследуя экстремальные свойства функции на границе, необходимо решить задачу определения условного экстремума.
Условный экстремум. Пусть необходимо найти экстремум функции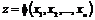 
, при условии, что переменные x, x, …, xудовлетворяют уравнениям
. (8)
Предполагается, что функции имеют непрерывные частные производные по всем переменным. Уравнения (8) называют уравнениями связи.
Говорят, что в точке 
, удовлетворяющей уравнениям связи (8), функция имеет условный максимум (минимум), если неравенство () имеет место для всех точек X, координаты которых удовлетворяют уравнениям связи.
Легко заметить, что задача определения условного экстремума совпадает с задачей нелинейного программирования.
Один из способов определения условного экстремума применяется в том случае, если из уравнений связи (8) m переменных, например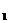, x, x, …, x
можно явно выразить через оставшиеся n-m переменных:
. (9)
Подставив полученные выражения для x
в функцию z, получим
или
. (10)
Задача сведена к нахождению локального (глобального) экстремума для функции (10) от n-m переменных. Если в точке 
функция (10) имеет экстремум, то в точке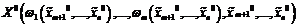 
функция 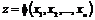имеет условный экстремум.
Задача 2. Решить задачу, максимизации производственной функции z, если функция z равна:
.
Решение. Необходимо найти переменные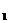 x и x, удовлетворяющие уравнению
(11)
(уравнению связи), условию неотрицательности 
и обращение в максимум функцию
(12)
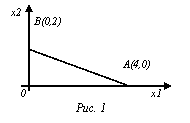Ограничение (11) вместе с условиями неотрицательности определяют на плоскости xOx отрезок 
- замкнутую ограниченную область (рис. 1)
Согласно теореме Вейерштрасса максимум функции может достигаться либо внутри этого отрезка, либо в граничных точках: А(4;0) или В(0;2).
Следовательно, необходимо найти условный экстремум функции (12), если уравнение связи имеет вид (11).
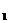Из уравнения связи найдем, например, x и подставим в (12): x=4-2x, 
.
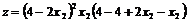Упростив, получим
. (13)
При этом x
. Найдем глобальный экстремум функции (13) на отрезке 
. Производная этой функции равна 
.
Стационарные точки: x=0, x=1 и x=2. Одна из них, x=1, лежит внутри отрезка, две другие совпадают с концами. Найдем значение функции (13) в стационарной точке x=1 и на концах отрезка: z(1)=4; z(0)=0; z(2)=0.
Следовательно, 
и достигается при x=1, x=4-2x=2, то есть в точке (2;1).
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Основные порталы (построено редакторами)