Таблица 5
Источник | Сток | Поставки | |||
1 | 2 | 3 | 4 | ||
1 2 3 | 5/с11 с21 с31 | 5/с12 5/с22 с32 | с13 | с14 | 0 0=5-5 15 |
с23 с33 | c24 с34 | ||||
Спрос | 0 | 0=5-5 | 8 | 7 |
|
В северо-западном углу незаштрихованной части табл. 5 находится переменное модели x23 и 0 = S2<D3 = 8. Поэтому полагаем x23=S2=0 и в табл. 5 заштриховываем вторую строку и после замены D3 на D3-S2= 8 приходим к табл.6
Таблица 6
Источник | Сток | Поставки | |||
1 | 2 | 3 | 4 | ||
1 2 3 | 5/с11 с21 с31 | 5/ с12 5/с22 с32 | с13 0/с23 | с14 с24 | 0 0=0-0 15 |
с33 | с34 | ||||
Спрос | 0 | 0 | 8=8-0 | 7 |
|
Табл. 6 содержит единственную незаштрихованную строку и из нее непосредственно следует, что x33=8 и x34=7. А та как значения свободных переменных равны нулю, то найден. начальное базисное решение, определяемое следующими значениями базисных переменных: x11=5, x12=5, x22=5, x23=0, x33=8, x34=7.
Кроме правила северо-западного угла разработаны и другие процедуры нахождения начального базисного решения для классической транспортной задачи. Остановимся лишь на одной из них, известной в исследовании операций как метод минимальной стоимости. Единственное отличие этого метода от метода северо-западного угла заключается в том, что при его реализации используют переменное xij, которому соответствует минимальная удельная стоимость cij, а не переменное модели, расположенное в северо-западном углу транспортной таблицы.
Задача 2. Пусть классическая транспортная задача, для которой необходимо найти начальное базисное решение, представлена своей транспортной таблицей (табл.7).
Минимальной удельной стоимости c22=0 соответствует переменное модели x22. А так как в данном случае 1 = S2<D2 = 5, то полагаем x22=1, заменяем D2 на, D2- S2=4 и после штриховки второй строки приходим к табл.8.
Таблица 7
Источник | Сток | Поставки | |||
1 | 2 | 3 | 4 | ||
1 2 3 | x11/ 2 x21 /1 x31 /5 | x12 /3 x22 /0 x32 /8 | x13/11 x23/ 6 x33/15 | x14/ 7 x24/ 1 x34 /9 | 6 1 10 |
Спрос | 7 | 5 | 3 | 2 |
|
Таблица 8
Источник | Сток | Поставки | |||
1 | 2 | 3 | 4 | ||
1 2 3 | x11/ 2 | x12/ 3 | x13/11 | x14/ 7 | 6 0=1-1 10 |
x21 /1 | 1 / 0 | x23/6 | x24/ 1 | ||
x31 /5 | x32 /8 | x33/15 | x34 /9 | ||
Спрос | 7 | 4=5-1 | 3 | 2 |
|
В незаштрихованной части табл. 8 минимальной удельной стоимости c11=2 соответствует переменное x11. В данном случае 6 = S1<D1=7. Поэтому полагаем x11=6, заменяем D1 на D1-S1=1 и после штриховки первой строки приходим к табл.9.
Табл. 9 представляет собой транспортную таблицу с одной незаштрихованной строкой. Поэтому x31=1, x32=4, x33=3, x34=2.
Таким образом, начальное базисное решение рассматриваемой классической транспортной задачи определяется следующими значениями переменных: x11=6, x22=1, x31=1, x32=4, x33=3, x34=2.
Таблица 9
Источник | Сток | Поставки | |||
1 | 2 | 3 | 4 | ||
1 2 3 | 6/ 2 x21 /1 | x12/ 3 1/ 0 | x13/11 x23/ 6 | x14/ 7 x24/ 1 | 0=6-6 0 10 |
x31 /5 | x32 /8 | x33/15 | x34 /9 | ||
Спрос | 1=7-6 | 4 | 3 | 2 |
|
Условимся называть систему линейных алгебраических уравнений треугольной, если она содержит по крайней мере одно уравнение с единственным неизвестным, при исключении которого опять найдется по крайней мере одно уравнение с единственным неизвестным, и так далее, пока не будут исчерпаны все неизвестные.
Теорема. Все допустимые базисные решения классической транспортной задачи задаются треугольной системой линейных алгебраических уравнений.
Множество W, пар индексов (i, j), соответствующих базисным переменным, содержит m+n-1 элементов, и можно показать, что система m + n — 1 линейных уравнений
![]() (5)
(5)
всегда разрешима относительно m + n неизвестных ui, ![]() , и
, и ![]() . При ее решении, как правило, независимому неизвестному придают нулевое значение.
. При ее решении, как правило, независимому неизвестному придают нулевое значение.
Решив систему линейных алгебраических уравнений (5) и определив значения симплекс-множителей, можно найти значения для коэффициентов при свободных переменных в левой части равенства (6). Уменьшить значение целевой функции, соответствующей исходному допустимому базисному решению, можно путем введения в базис рассматриваемой задачи линейного программирования лишь того свободного переменного xij, для которого dij<0, где
![]() (6)
(6)
При этом естественно выбирать то свободное переменное, для которого отрицательный коэффициент будет наибольшим по модулю. Если же коэффициенты при всех свободных переменных будут неотрицательными, то уменьшить значение целевой функции невозможно и исходное допустимое базисное решение является оптимальным решением.
Задача 3. Продолжим рассмотрение классической транспортной задачи, начатое в задаче 2. Для этой задачи найдено начальное допустимое базисное решение, характеризуемое значениями базисных переменных модели x11=6, x22=1, x31=1, x32=4, x33=3, x34=2 и значением целевой функции 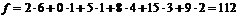
Воспользовавшись этими результатами и данными, представленными в табл. 12 выписываем систему линейных алгебраических уравнении (5):
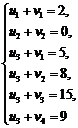
и находим симплекс-множители в предположении, что u3= 0:
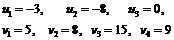
Используя полученные значения симплекс-множителей и известные удельные стоимости {сij}, представленные в табл. 12 вычисляем коэффициенты при свободных переменных согласно (6):
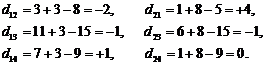
В новое допустимое базисное решение удобно ввести свободное переменное x12, так как |d12| = max{|d12|, |d13|, |d23|}.
Теперь необходимо найти то базисное переменное, которое должно быть выведено из базиса. В симплекс-методе реализация этого шага связана с условием допустимости выбора. Для уяснения идеи, используемой в симплексном методе при определении базисного переменного, выводимого из базиса, предположим, что при введении в базис свободного переменного x12 оно примет значение w>0. В этом случае для сохранения ограничения по первой строке транспортной таблицы значение базисного переменного x11 должно уменьшиться на w, т. е. x11=6—w. Но тогда для сохранения ограничения по первому столбцу транспортной таблицы значение базисного переменного x31 должно увеличиться на w, т. е. x31=1 +w. В этом случае для сохранения ограничений по третьей строке и второму столбцу транспортной таблицы значение базисного переменного x32 должно уменьшиться на ш, т. е. x32=4—w. Схема проведенных рассуждений представлена в табл. 10 в которой опущены значения сij
Таблица 10
Источник | Сток | Поставки | |||
1 | 2 | 3 | 4 | ||
1 2 3 | 6- 1+ |
4- | 6 1 10 | ||
Спрос | 7 | 5 | 3 | 2 |
С ростом x12=w>0 базисные переменные x11=6—w и x32=4—w будут уменьшаться. Следовательно, максимально возможное значение x12 равно 4, так как при этом значении w базисное переменное x32 принимает нулевое значение. При дальнейшем увеличении значений w базисное переменное x32 становится отрицательным, что противоречит требованию неотрицательности переменных. Следовательно, значение нового базисного переменного x12 равно 4, а переменное x32 должно быть выведено из базиса.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
 Основные порталы (построено редакторами)
Основные порталы (построено редакторами)

