Заметим, что основным переменным задачи С соответствуют дополнительные переменные задачи C* и наоборот.
Каноническая задача минимизации.
K. Найти решение системы
ai1y1+…+ainyn=bi (i=
) (I)
y1³0, …, yn³0,
которое минимизирует линейную форму g1y1+…+gnyn.
Задача, двойственная к задаче K:
K*. Найти решение системы
a1kzk+…+amkzk≤gk, (k=
), (II)
которое максимизирует линейную форму b1z1+…+bmzm.
Теорема 1. Если обе взаимно двойственные задачи допустимы, то обе задачи имеют решения и значения этих задач совпадают. Если хотя бы одна из задач недопустима, то ни одна из задач не имеет решений.
Теорема 2. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих значениях переменных линейной функции исходной задачи, выраженной через неосновные переменные ее оптимального решения.
1. 2. Модели целочисленного линейного программирования
Задача линейного программирования формулируется следующим образом: найти такое решение (план) X (x
,x
,…,x
), при которой линейная функция
(1)
принимает наибольшее (наименьшее) значение при ограничениях
(2)
(3)
- целые числа (4)
Методы целочисленной оптимизации можно разделить на три основные группы:
1) методы отсечения;
2) комбинаторные методы;
3) приближенные методы.
Методы отсечения
Один из алгоритмов решения задачи линейного целочисленного программирования (1)-(4), предложенный Гомори, основан на симплексном методе и использует достаточно простой способ построения правильного отсечения.
Пусть задача линейного программирования (1)-(3) имеет конечный оптимум, и на последнем шаге ее решения симплексным методом получены следующие уравнения, выражающие основные переменные 
через неосновные переменные 
оптимального решения
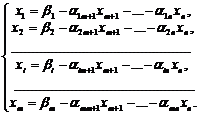(5)
так, что оптимальным решением задачи (1)-(3) является 
, в котором, например, 
- нецелая компонента. В этом случае легко доказать, что неравенство
(6)
сформированное по i-му уравнению системы (5), обладает всеми свойствами правильного отсечения.
Для решения задачи целочисленного линейного программирования (1)-(4) методом Гомори используется следующий алгоритм:
1) Симплексным методом решить задачу (1)-(3) без учета условия целочисленности. Если все компоненты оптимального плана целые, то он является оптимальным и для задачи целочисленного программирования (1)-(4). Если первая задача (1)-(3) неразрешима (т. е. не имеет конечного оптимума или условия ее противоречия), то и вторая задача (1)-(4) также неразрешима.
2) Если среди компонент оптимального решения есть нецелые, то выбрать компоненту с наибольшей целой частью и по соответствующему уравнению системы (5) сформировать правильное отсечение (6).
3) Неравенство (6) введением дополнительной неотрицательной целочисленной переменной преобразовать в равносильное уравнение и включить его в систему ограничений (2).
4) Полученную расширенную задачу решить симплексным методом. Если найденный оптимальный план будет целочисленным, то задача целочисленного программирования (1)-(4) решена. В противном случае вернуться в пункт 2 алгоритма.
Если задача разрешима в целых числах, то после конечного числа шагов (операций) оптимальный целочисленный план будет найден.
Если в процессе решения появится уравнение (выражающее основную переменную через неосновные) с нецелевым свободным членом и целыми остальными коэффициентами, то соответствующее уравнение не имеет решения в целых числах. В этом случае и данная задача не имеет целочисленного оптимального решения.
Задача. Имеется достаточно большое количество бревен длиной 3 м. Бревна следует распилить на заготовки двух видов: длиной 1,2 м и длиной 0,9 м, причем заготовок каждого вида должно быть получено не менее 50 шт. и 81 шт. соответственно. Каждое бревно можно распилить на указанные заготовки несколькими способами:
1) на 1 заготовку по 1,2 м и 2 заготовки по 0,9 м;
2) на 2 заготовки по 1,2 м;
3) на 3 заготовки по 0,9 м.
Найти число бревен, распиливаемых каждым способом, с тем, чтобы заготовок любого вида было получено из наименьшего числа бревен.
Решение. Обозначим через x1, x2, x3 число бревен, распиливаемых соответственно 1-м, 2-м и 3-м способами. Из них можно получить 2x1 + x2 заготовок по 1,2 м и 2x2+3x3 заготовок по 0,9 м. Общее количество бревен обозначим z. Тогда математическая модель задачи примет вид:
(1’’)
при ограничениях:
(2’’)
(3’’)
xj - целые числа. (4’’)
Введя дополнительные переменные 
, 
приведем систему неравенств к равносильной системе уравнений:
(5’’)
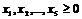
Решая полученную каноническую задачу (без условия целочисленности) симплексным методом, на последнем, 3 шаге решения, найдем следующие выражения основных переменных и линейной функции через неосновные переменные (рекомендуем получить их самостоятельно):
3 шаг. Основные переменные x1, x2; неосновные переменные x3, x4, x5.
,
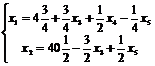
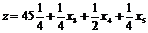т. е.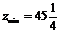 
при оптимальном решении X3 (4
;40
;0;0;0).
Получили, что две компоненты оптимального решения 
и 
не удовлетворяют условию целочисленности (4’’), причем большую целую часть имеет компонента x2. В соответствии с п. 2 алгоритма решения задачи целочисленного программирования по повторному уравнению, содержащему эту переменную x2, составляем дополнительно ограничение (6):
.
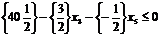Найдем дробные части 
; 
; 
.
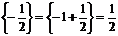Запишем последнее неравенство в виде
(6’’)
Введя дополнительную переменную 
, получим равносильное неравенству (6’’) уравнение:
(7’’)
Выразим из (7’’) дополнительную переменную x6 и полученное уравнение введем в систему ограничений, которую мы имели на последнем, 3 шаге, решения задачи (1’’)-(3’’) (без условия целочисленности). Имеем:
4 шаг. Основные переменные x1, x2, x6 ; неосновные переменные x3, x4, x5.
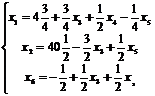
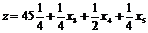
решая эту расширенную задачу симплексным методом (предлагаем студентам выполнить самостоятельно), получим на последнем, 5 шаге:
5 шаг. Основные переменные x1, x2, x3; неосновные переменные x4, x5; x6.
,
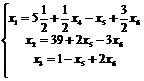
т. е.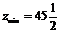 
при оптимальном решении X5 (5;39;1;0;0;0).
Полученное оптимальное решение расширенной задачи (1’’)-(3’’), (6’’), вновь не удовлетворяет условию целочисленности (4’’). По первому уравнению с переменной x1, получившей нецелочисленное значение в оптимальном решении (5
), составляем второе дополнительное ограничение (6):
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Основные порталы (построено редакторами)