Максимальный объем производства, равный 
достигается при условии, что затраты производственных факторов 1-го и 2-го типа равны соответственно 2 ед. и 1 ед.
Второй способ определения условного экстремума начинается с построения вспомогательной функции Лагранжа, которая в области допустимых решений достигает максимума для тех же значений переменных x
,x
,…, x
, что и целевая функция z.
Пусть решается задача определения условного экстремума функции 
при ограничениях (8).
Составим функцию
, (14)
которая называется функцией Лагранжа. 
- постоянные множители (множители Лагранжа). Отметим, что множителям Лагранжа можно придать экономический смысл. Если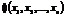 
, - доход, соответствующий плану 
, а функция 
- издержки i-го ресурса, соответствующие этому плану, то
цена (оценка) i-го ресурса, характеризующая изменение экстремального значения целевой функции в зависимости от изменения размера i-го ресурса (маргинальная оценка). L(X) – функция n+m переменных x,x,…, x, 
. Определение стационарных точек этой функции приводит к решению системы уравнений:
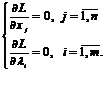(15)
Легко видеть, что 
, т. е. в (15) входят уравнения связи. Таким образом, задача нахождения условного экстремума функции 
сводится к нахождению локального экстремума функции L(X). Если стационарная точка найдена, то вопрос о существовании экстремума в простейших случаях решается на основании достаточных условий экстремума – исследования знака второго дифференциала d
L(X) в стационарной точке при условии, что переменные приращения 
связаны соотношениями:
, (16)
полученными путем дифференцирования уравнений связи.
Задача. Найти наибольшее значение функции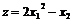 
при ограничениях:
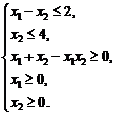
Решение. ОДР ограничена прямыми 
, осями координат 
и гиперболой 
, уравнение которой приводится к виду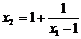 
.
Линии уровня целевой функции 
. Для разных значений C графиком уравнения 
является парабола с осью симметрии, совпадающей с осью ординат.
При C=0 парабола проходит через начало координат. При C>0 параболы сдвигаются вниз. Перемещая в направлении возрастания C, получим, что линии уровня покидают ОДР через точку X* пересечения гиперболы 
и прямой 
.
Решая систему, составленную из этих двух уравнений, получим:
, 
; 
.
или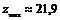 
.
Применение классических методов имеет некоторые трудности. Поэтому разработаны приближенные методы решения нелинейных задач программирования, особенно плодотворные для некоторых классов функций, например, для выпуклых (вогнутых) функций.
3. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ПРЕПОДАВАТЕЛЯ ПО ПРАКТИЧЕСКИМ, СЕМИНАРСКИМ ЗАНЯТИЯМ, ЛАБОРАТОРНЫМ РАБОТАМ И ДРУГИМ ВИДАМ ЗАНЯТИЙ
Методические указания к практическим занятиям
Задача линейного программирования
Оптимизационные (экстремальные) модели в экономике возникают при практической реализации принципа оптимальности в управлении.
Выбор оптимального управленческого поведения в конкретной ситуации связан с проведением экономико-математического моделирования и решением задачи оптимального программирования, в простейшем случае — задачи линейного программирования.
В наиболее общем виде задача (модель) линейного программирования записывается следующим образом: требуется найти экстремум (максимум или минимум) линейной целевой функции: f(x1, х2,…, хn) = c1х1+ c2 х2+…+ cnхn
при ограничениях:
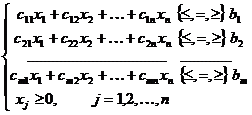
где ci,j , bi (i=1,2,…,m; j=1,2,…,n) — заданные постоянные величины.
Иногда невозможно получить решение по оптимизационной модели: область допустимых решений может оказаться пустым множеством (система ограничений задачи противоречива) или целевая функция является неограниченной на области определения.
Первый случай связан с некорректностями в постановке экономической задачи и (или) разработанной ЭММ. Например, имеющимся объемом ресурсов заведомо невозможно выполнить даже те минимальные объемы работ, которые закладываются в ограничения как необходимые минимальные плановые задания. Если в данной ситуации все же необходимо найти решение задачи, то следует построить непустое множество допустимых решений, исключив одно или несколько ограничений, т. е. фактически соблюсти принцип альтернативности.
Второй случай обычно означает, что ЭММ разработана некорректно, и некоторые существенные ограничения в ней отсутствуют.
Примеры задачи линейного программирования
Задача линейного программирования в том или ином виде интерпретируется как задача об оптимальном использовании ограниченных производственных ресурсов.
Задача. Найти решение ЗЛП
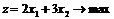
при ограничениях
,
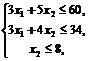
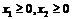Решение. Приведем задачу к каноническому виду, введя дополнительные неотрицательные переменные x3,, x4,, x5. Получим систему ограничений
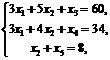
xj³0, j=1,2,…,5
Решаем систему симплексным методом поэтапно.
Введем основные (базисные, связанные) и неосновные (свободные, принимающие нулевые значения) переменные. Базисные переменные выразим через неосновные.
1 шаг. Основные переменные x3, x4, x5; неосновные переменные x1, x2.
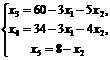
Первое базисное решение: X1 (0;0;60;34;8) – допустимое. Соответствующее значение линейной функции z1=0.
Переводим в основные переменную x2, которая входит в выражение линейной функции с наибольшим положительным коэффициентом. Находим максимально возможное значение переменной x2, которое «позволяет» принять система ограничений, из условия минимума соответствующих отношений:
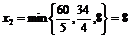
т. е. разрешающим (выделенным) является третье уравнение. При x2=8 в этом уравнении x5=0, и в неосновные переходит переменная x5.
2 шаг. Основные переменные x2, x3, x4; неосновные переменные x1, x5
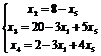
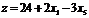
Первое базисное решение: X2 (0;8;20;2;0) – допустимое. Соответствующее значение линейной функции z2=24. Переводим в основные переменную x1,
,
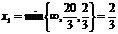а в неосновные x4.
3 шаг. Основные переменные x1, x2, x3; неосновные переменные x4, x5.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Основные порталы (построено редакторами)