· установим флажки:
ü Линейная модель (это обеспечит применение симплекс-метода)
ü Неотрицательные значения, так как значение работника на должность принимает значение «1» или «0» , т. е. отрицательной величиной быть не может;
· кнопка ОК.
· кнопка Выполнить.
7. Просмотр результатов и печать отчета. После выполнения всех вышеуказанных действий на экран выводится окно Результаты поиска решения
· В окне Тип отчета выбрать интересующий вид отчета.
· кнопка ОК.
Внизу страницы экрана содержится сообщение Отчет по результатам 1. Щелкнуть на этом сообщении, на экран выводятся результаты решения задачи, которые можно распечатать.
При нажатии Лист 1 происходит возврат в программу, к исходным данным.
В Матрице назначений содержится схема распределения работников по должностям (1 – назначен, 0 – не назначен), дающая максимальную суммарную производительность труда, Значение целевой функции содержится в ячейке В16 и для конкретной задачи равно 22.
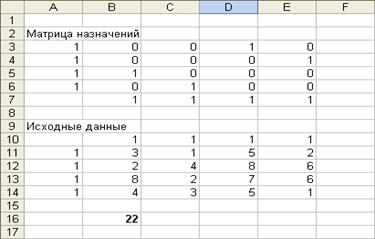
Вывод: максимум производительности труда, равный 22 условных единицы, будет достигнут при назначении:
1. первого работника на должность В3 (содержимое ячейки DЗ = 1);
2. второго работника на должность В4 (Е4=1);
3. третьего работника на должность В1 (В5=1);
4. четвертого работника на должность В2 (С6=1).
Задачи для самостоятельного решения
1. Решите транспортную задачу, определив минимальную стоимость перевозки грузов
Мощности поставщиков | Мощности потребителей | |||
22 | 34 | 41 | 20 | |
31 | 10 | 7 | 6 | 8 |
48 | 5 | 6 | 5 | 4 |
38 | 8 | 7 | 6 | 7 |
2. Перед менеджером стоит задача распределения четырех работников по вакантным должностям по условиям результатов контрольных испытаний. Производительность труда по отдельным видам работ, показанная каждым из работников, приведена в таблице.
Одним из основных условий поставленной задачи является максимизация производительности труда в коллективе при условии, что каждый работник может быть назначен только на одну работу.
Работники | Производительность труда работников по должностям | |||
В1 | В2 | В3 | В4 | |
А1 | 9 | 6 | 5 | 8 |
А2 | 4 | 8 | 6 | 2 |
А3 | 6 | 7 | 9 | 4 |
А4 | 2 | 7 | 3 | 1 |
Чему равен максимум производительности труда?
3. Для строительства 4 дорог необходим гравий в количестве 130, 220, 60 и 70 единиц, который может быть поставлен из 3 карьеров, запасы которых составляют120,280 и 160 единиц соответственно, а тарифы перевозок представлены таблицей. Определите минимальные затраты перевозки гравия.
1 | 7 | 9 | 5 |
4 | 2 | 6 | 8 |
3 | 7 | 1 | 2 |
нелинейное программИРОВАНИЕ
Задача (модель) нелинейного программирования (НЛП) формулируется так же, как и общая задача оптимального программирования со следующими требованиями к целевой функции (ЦФ) и допустимой области:
ЦФ f(х1, х2,…, хn) и (или) одна из функций g(х1, х2,…, хn) являются нелинейными:
min (max) f(х1, х2,…, хn);
g(х1, х2,…, хn) {≤¸=¸≥} bi , i= 1,…, m; xj ≥0, j=1, …, n.
У произвольной задачи НЛП некоторые или все свойства, характерные для задач ЛП, отсутствуют. Вследствие этого задачи НЛП несравнимо сложнее задач ЛП, и для них не существует общего универсального метода их решения (аналогично симплексному методу).
Примеры задач нелинейной оптимизации
Задача. Найти наибольшее и наименьшее значение функции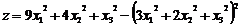 
при условии, что x1, x2, x3 удовлетворяют уравнению 
.
Решение. Уравнение связи определяет в пространстве сферу единичного радиуса с центром в начале координат (рис. 1).
Так как сфера – замкнутое ограниченное множество, то согласно теореме Вейерштрасса функция достигает на ней своего наибольшего и наименьшего значений.
Необходимо найти условный глобальный экстремум. Запишем уравнение связи в виде: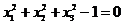 
.
Составим функцию Лагранжа:
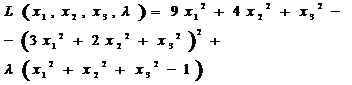
Найдем частные производные этой функции по 
.
Приравняв частные производные нулю, получим систему:
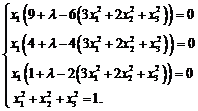
Решая систему, получим стационарные точки, в которых найдем значения функции z. Все решения удобно перенумеровать:
1) 
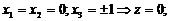
2) 
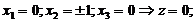
3) 
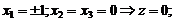
4) 
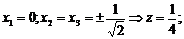
5) 
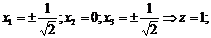
6) 
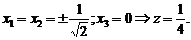
выберем из всех значений z наименьшее и наибольшее: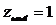 
; 
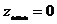. Легко видеть, в каких точках сферы достигаются эти значения.
Если число переменных n равно двум, нелинейные задачи можно решать геометрически. Ограничения должны быть записаны в виде неравенств:
, (1)
а целевая функция имеет вид:
. (2)
Как и в случае геометрического решения задач линейного программирования, сначала необходимо построить область допустимых решений (ОДР) – множество точек плоскости, удовлетворяющих неравенствам (1). Но в отличие от задач линейного программирования ОДР не обязательно будет выпуклой, может быть даже разрывной. Экстремум функции может достигаться и внутри области, и на границе.
После построения ОДР следует записать уравнения линий уровня целевой функции – множество точек плоскости, в которых целевая (2) функция постоянна: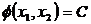 
, и определить направление возрастания (убывания) целевой функции, построив, например, линии уровня для разных значений C. Затем, перемещая линию уровня в нужном направлении в ОДР, найти точки области, в которых целевая функция принимает оптимальное значение.
В пакете Ехсеl реализован метод множителей Лагранжа, идея которого заключается в преобразовании задачи условной оптимизации в задачу безусловной оптимизации, решение которой производится методами поиска – градиентными методами (методы первого порядка) или методами Ньютона (методы второго порядка). Наиболее распространенными являются градиентные методы.
Существующие методы дают возможность находить только локальные оптимумы (помимо случаев, когда задачи обладают соответствующими свойства ми выпуклости и вогнутости). Если же есть подозрение, что в допустимой области ЦФ может иметь несколько оптимумов, эту область следует разбить на ряд областей и в каждой из них определить свои локальные оптимумы, а затем из всех локальных оптимумов выбрать глобальный. В таком практическом подходе задача поиска глобального оптимума сводится к решению ряда задач, в которых ищется свой (локальный) оптимум.
Следует отметить, что в подавляющем большинстве практических задач оптимизации существует только один оптимум.
Решение задачи НЛП (реализация модели нелинейной оптимизации) средствами Ехсеl отличается от решения ЗЛП следующим:
– назначаются начальные значения искомых переменных х0j, j= 1,…, п так, чтобы ЦФ в начальной точке не была равна нулю, f(х01, х02,…, х0n)≠0;
– в диалоговом окне Поиск решения в режиме Параметры не надо вводить Линейная модель.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Основные порталы (построено редакторами)