42. Концепция логистического подхода к управлению запасами
43. Затраты, связанные с управлением запасами
44. Дайте постановку однопродуктовой статической модели управления запасами
45. Дайте постановку многопродуктовой статической модели управления запасами
46. Дайте постановку однопродуктовой статической модели управления запасами с разрывами цен
47. Дайте постановку однопродуктовой динамической модели управления запасами
48. Перечислите системы контроля уровня запасов
49. Перечислите типы систем массового обслуживания
50. Расскажите о модели EOQ. Когда и кем впервые были проведены исследования?
51. ABC - система управления запасами
52. Где применяется система управления запасами JIT?
53. Дайте определение марковского процесса
54. Раскройте смысл уравнений Колмогорова
55. Перечислите основные компоненты системы массового обслуживания
56. Что такое эффективность функционирования систем массового обслуживания
57. Раскройте смысл моделей размножения и гибели
58. Приведите классификацию систем массового обслуживания
59. Для каких целей используют формулу Литтла
60. Перечислите свойства потока систем массового обслуживания
61. Для каких целей используют формулу Эрланга
62. Перечислите и дайте определения основным элементам теории нечетких множеств
63. Дайте определение нечетким операциям, отношениям и свойствам отношений
64. Приведите постановку задачи многокритериального выбора альтернатив (МВА) на основе пересечения нечетких множеств
65. Приведите постановку задачи МВА на основе нечеткого отношения предпочтения
66. Приведите постановку задачи МВА с использованием правил нечеткого вывода
67. Приведите постановку задачи МВА на основе аддитивной свертки
68. Разработайте алгоритмы и программы для решения вопросов для решения задач МВА на основе пересечения нечетких множеств, на основе нечеткого отношения предпочтения, с использованием правил нечеткого вывода, на основе аддитивной свертки.
69. Решите задачу «МВА в сфере банковского кредитования» различными методами принятия решений, основанными на теории нечетких множеств. Проведите сравнительный анализ полученных результатов.
70. Решите задачу «МВА в сфере банковского кредитования» различными методами принятия решений, основанными на теории нечетких множеств и методах анализа иерархий. Приведите сравнительный анализ полученных результатов.
7 Методические указания для обучающихся по освоению
дисциплины (модуля) « Методы оптимальных решений »
КРАТКИЕ КОНСПЕКТ ЛЕКЦИЙ
1. Модели линейного программирования
В наиболее общем виде задача (модель) линейного программирования записывается следующим образом: требуется найти экстремум (максимум или минимум) линейной целевой функции: f(x1, х2,…, хn) = a1х1+ a2 х2+…+ anхn
: 
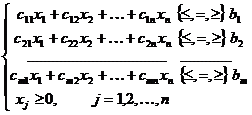
где ci,j , bi (i=1,2,…,m; j=1,2,…,n) — заданные постоянные величины.
Задача линейного программирования (ЗЛП) задана в канонической форме, если в системе ограничений заданы только равенства и в стандартной, если неравенства.
Геометрический метод решения задачи линейного программирования
Данный метод применяется, в основном, при решении ЗЛП с двумя переменными.
Теорема 1. Множество решений неравенства с двумя переменными a1x1+a2 x2≤b является одной из двух полуплоскостей, на которые вся плоскость делится прямой a1x1+a2 x2=b, включая и эту прямую, а другая полуплоскость с той же прямой есть множество решений неравенства a1x1+a2 x2≥b.
Обобщая данную теорему на случай n переменных, имеем: Множество всех решений линейного неравенства с n переменными является одним из полупространств, на которые все пространство делится плоскостью или гиперплоскостью, включая и эту плоскость (гиперплоскость).
Теорема 2. Множество решений совместной системы т линейных неравенств с двумя переменными
a 11x1+a1 2 x2≤b1
a 21x1+a2 2 x2≤b2
………….
a n1x1+an 2 x2≤bn
является выпуклым многоугольником (или выпуклой многоугольной областью).
Теорема 3. Множество всех допустимых решений совместной системы m линейных уравнений с n переменными (m<n) является выпуклым многогранником (выпуклой многогранной областью) в n-мерном пространстве.
Теорема 4. Если задача линейного программирования имеет оптимальное решение, то линейная функция принимает максимальное значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное значение более чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинацией этих точек.
Любые m переменных системы m линейных уравнений с n переменными (m <n) называются основными (или базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные n-m переменных называются неосновными (или свободными).
Если для системы m линейных уравнений с n переменными (m <n) ранг матрицы коэффициентов при переменных равен m, т. е. существует хотя бы одна группа основных переменных, то эта система является неопределенной, причем каждому произвольному набору значений неосновных переменных соответствует одно решение системы.
Среди бесконечного множества решений системы выделяют так называемые базисные решения.
Базисным решением системы m линейных уравнений с n переменными называется решение, в котором все n-m неосновных переменных равны нулю. Базисное решение является допустимым, если все его компоненты неотрицательны. Допустимое базисное решение называется оптимальным, если целевая функция на нем принимает свое оптимальное значение.
Теорема 5. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка многогранника решений, и наоборот, каждой угловой точке многогранника решений соответствует допустимое базисное решение.
Симплексный метод решения ЗЛП
Данный метод рассмотрим на примере.
Задача. Найти решение ЗЛП
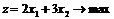
при ограничениях
,
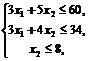
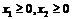Решение. Приведем задачу к каноническому виду, введя дополнительные неотрицательные переменные x3,, x4,, x5. Получим систему ограничений
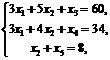
xj³0, j=1,2,…,5
Решаем систему симплексным методом поэтапно.
Введем основные (базисные, связанные) и неосновные (свободные, принимающие нулевые значения) переменные. Базисные переменные выразим через неосновные.
1 шаг. Основные переменные x3, x4, x5; неосновные переменные x1, x2.
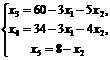
Первое базисное решение: X1 (0;0;60;34;8) – допустимое. Соответствующее значение линейной функции z1=0.
Переводим в основные переменную x2, которая входит в выражение линейной функции с наибольшим положительным коэффициентом. Находим максимально возможное значение переменной x2, которое «позволяет» принять система ограничений, из условия минимума соответствующих отношений:
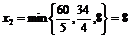
т. е. разрешающим (выделенным) является третье уравнение. При x2=8 в этом уравнении x5=0, и в неосновные переходит переменная x5.
2 шаг. Основные переменные x2, x3, x4; неосновные переменные x1, x5
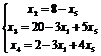
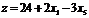
Первое базисное решение: X2 (0;8;20;2;0) – допустимое. Соответствующее значение линейной функции z2=24. Переводим в основные переменную x1,
,
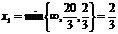а в неосновные x4.
3 шаг. Основные переменные x1, x2, x3; неосновные переменные x4, x5.
.
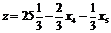X3 (
;8;18;0;0); 
Базисное решение X3 оптимальное для задачи.
(
), так как в выражении линейной функции отсутствуют неосновные переменные с положительными коэффициентами.
Двойственные задачи
Основными задачами теории линейного программирования являются стандартные и канонические задачи на минимум и максимум.
Стандартная задача минимизации.
C. Найти решение системы
ai1y1+…+ainyn≥bi (i=
) (1)
y1³0, …, yn³0,
которое минимизирует линейную форму g1y1+…+gnyn.
Стандартная задача максимизации.
a1kzk+…+amkzk≤gk, (k=
), (2)
z1³0,…, zm³0,
которое максимизирует линейную форму b1z1+…+bmzm.
Условия (1) и (2) называются линейными ограничениями задач C и C* соответственно. Задачи C и C* называются взаимно двойственными.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Основные порталы (построено редакторами)