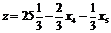 .
.
X3 (![]() ;8;18;0;0);
;8;18;0;0); ![]()
Базисное решение X3 оптимальное для задачи.
( ), так как в выражении линейной функции отсутствуют неосновные переменные с положительными коэффициентами.
), так как в выражении линейной функции отсутствуют неосновные переменные с положительными коэффициентами.
Основным методом решения ЗЛП является симплекс-метод. Именно этот метод реализован в программе Поиск решения пакета Ехсеl.
Первым шагом при работе с командой (программой, надстройкой) Сервис/Поиск решения является создание специального (рабочего) листа, т. е. специальная запись ЭММ в терминах электронной таблицы (ЭТ) Ехсеl.
Для этого необходимо создать в рабочем листе Ехсеl целевую ячейку, в которой записывается целевая функция моделей, а также одну или несколько изменяемых (переменных) ячеек, которые, как правило, отвечают управляющим переменным в модели и значения которых могут изменяться для достижения экстремума (максимума или минимума) целевой функции. Для успешного поиска решения необходимо, чтобы каждая из переменных ячеек влияла на целевую ячейку (другими словами, формула в целевой ячейке должна опираться в вычислениях на значения переменных ячеек). В противном случае при выполнении команды Поиск решения появляется сообщение об ошибке: Результаты целевой ячейки не сходятся.
Ограничения модели записываются в соответствующих ячейках в виде значений, которые должны находиться в определенных пределах или удовлетворять граничным условиям. Ограничения могут налагаться как на целевую, так и на переменные ячейки (по два ограничения для каждой изменяемой ячейки с указанием верхнего и нижнего пределов, а также до ста дополнительных). Таким образом, на специальном листе должны содержаться ячейки, в которых вычисляются ограничиваемые величины. Тип каждого из ограничений модели (≤,=,≥) задается (вводится) в специальном окне диалога при выполнении команды Поиск решения. Численные значения самих ограничений включать в специализированный лист необязательно – они также вводятся в специальном окне диалога при выполнении команды Поиск решения. В режиме Параметры окна диалога Поиск решения задается тип модели (линейная или нелинейная).
После команды Выполнить диалогового окна Поиск решения осуществляется поиск оптимального решения – в итоге появляется диалоговое окно Результаты поиска решения.
В режиме Справки этого диалогового окна содержатся сведения об итоговых сообщениях процедуры поиска решения. Например, в случае несовместности системы ограничений Ехсеl будет выдавать сообщение Поиск не может найти подходящего решения. Если же решение задачи отсутствует вследствие неограниченности целевой функции на множестве допустимых решений, то Ехсеl будет выдавать сообщение Значения целевой ячейки не сходятся. При успешном завершении решения задачи появляется диалоговое окно Результат поиска решения. Решение найдено. С помощью вкладки Результаты этого диалогового окна можно получить отчет по результатам решения, вкладки Устойчивость и Пределы позволяют провести дополнительный экономико-математический анализ оптимального плана и подучить отчеты по устойчивости и по пределам.
Задача. Предприятие выпускает продукцию четырех видов П1, П2, П3, П4 с использованием для этого ресурсов, виды и нормы расхода по которым, а также уровень получаемой от их реализации прибыли приведены в таблице. Составьте оптимальный план производства продукции, дающий максимальную прибыль.
Вид ресурса | Вид продукции | Запас ресурса | |||
П1 | П2 | П3 | П4 | ||
Трудовые | 1 | 1 | 1 | 1 | 16 |
Сырье | 6 | 5 | 4 | 3 | 110 |
Оборудование | 4 | 6 | 10 | 13 | 100 |
Прибыль | 60 | 70 | 120 | 130 |
Экономико-математическая модель:
Введём необходимые обозначения: пусть xj (j=1,2,3,4) – объемы каждого вида продукции. Тогда ЭММ задачи запишется следующим образом:
max f(x1, x2, x3, x4) =60x1+70x2+120x3+130x4,
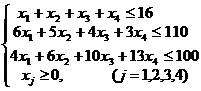
Решение.
1. Создадим форму для ввода условий задачи. Для этого запустим Excel, выбрав Microsoft Excel из подменю Программы главного меню Windows. Создадим текстовую форму – таблицу для ввода условий задачи.
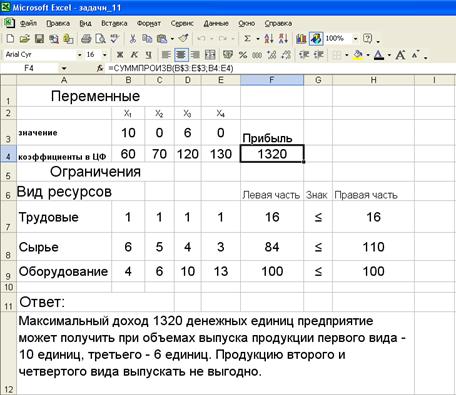
2. Укажем адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки). Значения компонент вектора X=(x1, x2, x3, x4) поместим в ячейках ВЗ:ЕЗ, оптимальное значение целевой функции – в ячейку F4.
3. Введем исходные данные задачи в созданную форму-таблицу:
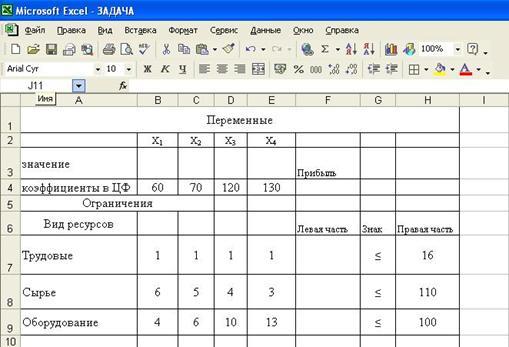
4.Введем зависимость для целевой функции:
· установить курсор в ячейку F4.
· кликнуть по кнопке Мастер функций, расположенной на панели инструментов.
· на экране появляется диалоговое окно Мастер функций – шаг 1 из 2.
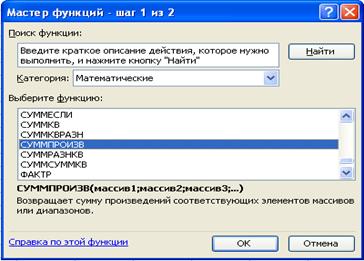
· выбрать категорию Математические;
· выбрать функцию СУММПРОИЗВ
· на экране появляется диалоговое окно СУММПРОИЗВ;
· в строку Массив 1 введем В$3:Е$3;
· в строку Массив 2 введем В4:Е4;
· кликнуть по кнопке ОК. На экране в ячейку F4 введена функция.
5. Ввести зависимости для ограничений:
· курсор в ячейку F4; кнопка Копировать;
· курсор в ячейку F7; кнопка Вставить;
· курсор в ячейку F8; кнопка Вставить;
· курсор в ячейку F9; кнопка Вставить.
В строке Меню установить указатель мыши на имя Сервис. В развернутом меню выбрать команду Поиск решения.
6. Назначим целевую функцию (установим целевую ячейку):
· курсор в строку Установить целевую ячейку;
· введем адрес ячейки $F$4;
· введем направление целевой функции в зависимости от условия задачи – Максимальному значению;
· курсор в строку Изменяя ячейки;
· введем адреса искомых переменных В$3:E$3.
7. Введем ограничения:
· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;
· в строке Ссылка на ячейку введем адрес $F$7: $F$9 (или укажем на листе, т. е. щелкнуть на маленькой красной стрелке рядом с этим полем, выйти в таблицу, выделить ячейки F7:F9, нажать клавишу F4, при этом ссылка станет абсолютной $F$7: $F$9, щелкнуть на красной стрелке и вернуться в блок Поиска решения, при этом нужный адрес будет введен);
· выберем знак ограничения <=;
· в строке Ограничения введем адрес $Н$7: $Н$9;
· после введения ограничения кнопка ОК.

8. Введем параметры для решения ЗЛП:
· в диалоговом окне Поиск решения кнопка Параметры.
· на экране диалоговое окно Параметры поиска решения
· установим флажки:
ü Линейная модель (это обеспечит применение симплекс-метода)
ü Неотрицательные значения;
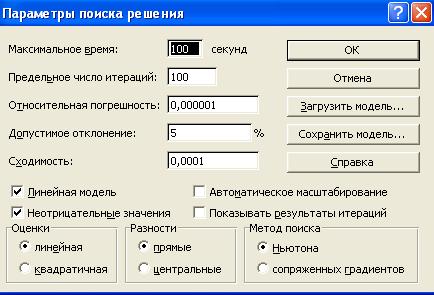
· кнопка ОК. На экране диалоговое окно Поиск решения;
· кнопку Выполнить.
· в диалоговом окно Результаты поиска решения
· выбрать Сохранить найденное решение
· кнопка OK
На экране представлена исходная таблица с заполненными ячейками ВЗ:ЕЗ для значений X и ячейка F4 с максимальным значением целевой функции. Введем экономическую интерпретацию полученных результатов: «Максимальный доход 1320 денежных единиц предприятие может получить при объемах выпуска продукции первого вида – 10 единиц, третьего вида – 6 единиц. Продукцию второго и четвертого вида выпускать не выгодно.»
Задача целочисленного линейного программирования
Задачи оптимизации, в результате решения которых искомые значения переменных должны быть целыми числами, называются задачами (моделями) целочисленного (дискретного) программирования:
min (max) f(x1 ,x2 ,…,xn);
gj (x1 ,x2 ,…,xn) {≤¸=¸≥} xj ≥0, j= 1, m
xj — целые неотрицательные ![]() < п'> .
< п'> .
Если множество индексов <п'> = <п > – {1, 2, ... , п} , то задачу называют полностью целочисленной, если <n'> ![]() <n>,то частично целочисленной.
<n>,то частично целочисленной.
Примеры задачи целочисленного линейного программирования
Задача. Решить задачу Z = 3x1 + x2 ® max при ограничениях:
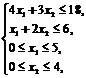
х1, х2 – целые числа.
Решение. За нижнюю границу линейной функции примем, например, ее значение в точке (0,0), т. е. Z0= Z(0; 0) = 0.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
 Основные порталы (построено редакторами)
Основные порталы (построено редакторами)

