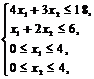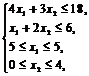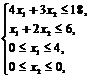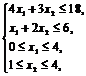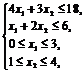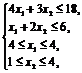I этап. Решая задачу симплексным методом, получим Zmax=13 при 
= (4,5; 0; 0; 1,5; 0,5; 4); так как первая компонента 
дробная, то из области решения исключается полоса, содержащая дробное оптимальное значение , т. е. 4<x1<5. Поэтому задача 1 разбивается на две задачи 2 и 3:
Задача 2 | Задача 3 |
Z = 3x1 + x2 ® max при ограничениях:
х1, х2 – целые числа. | Z = 3x1 + x2 ® max при ограничениях:
х1, х2 – целые числа. |
Список задач: 2 и 3. Нижняя граница линейной функции не изменилась: Z0=0.
II этап. Решаем (по выбору) одну из задач списка, например задачу 3 симплексным методом.
Получим, что условия задачи 3 противоречивы.
III этап. Решаем задачу 2 симплексным методом. Получим 
при 
. Хотя 
, по-прежнему сохраняется Z0=0, ибо план Х3 нецелочисленный. Так как 
- дробное число, из области решений исключаем полосу 0<x2<1 и задачу 2 разбиваем на две задачи 4 и 5.
Задача 4 | Задача 5 |
Z = 3x1 + x2 ® max при ограничениях:
х1, х2 – целые числа. | Z = 3x1 + x2 ® max при ограничениях:
х1, х2 – целые числа. |
Список задач: 4 и 5. Значение Z0=0.
IV этап. Решаем задачу 4 симплексным методом. Получим Zmax = 12 при 
= (4; 0; 2; 2; 0; 0). Задачу исключаем из списка, но при этом меняем Z0; Z0= Z()=12, ибо план целочисленный.
V этап. Решаем задачу 5 симплексным методом. Получим Zmax = 12,25 при 
=(3,75; 1; 0; 0,25; 0,25; 0; 3). Z0 не меняется, т. е. Z0=12, ибо план нецелочисленный. Так как - дробное, из области решений исключаем полосу 3<x1<4 и задача 5 разбивается на две задачи: 6 и 7.
Задача 6 | Задача 7 |
Z = 3x1 + x2 ® max при ограничениях:
х1, х2 – целые числа. | Z = 3x1 + x2 ® max при ограничениях:
х1, х2 – целые числа. |
Список задач: 6 и 7. Значение Z0=12.
VI этап. Решаем одну из задач списка, например задачу 7, симплексным методом.
Получим, что условия задачи 7 противоречивы.
VII этап. Решаем задачу 6 симплексным методом. Получим Zmax = 10,5 при 
=(3; 1,5; 1,5; 0; 0; 0,5; 2,5). Так как Z()=10,5 < Z0=12, то задача исключается из списка.
Итак, список задач исчерпан и оптимальным целочисленным решением исходной задачи будет Х* = = (4; 0; 2; 2; 0; 0), а оптимум линейной функции Zmax =12.
Существуют различные методы решения задач дискретного программирования (дискретной оптимизации). Наиболее часто используемым методом является метод ветвей и границ. Именно этот метод реализован в программе Поиск решения пакета Ехсеl.
Дискретная оптимизация средствами Ехсеl проводится аналогично решению соответствующих непрерывных задач. Основное отличие заключается во вводе при оформлении диалогового окна Поиск решения требования целочисленности соответствующих переменных (при этом в режиме Параметры устанавливается тип задачи - линейная или нелинейная).
Исходя из требования целочисленности в случае дискретной оптимизации возможен вызов только одного Отчета по результатам.
Достаточно часто при моделировании экономических процессов используется особый случай дискретности задачи - булевость переменных, т. е. переменные могут принимать значения 0 или 1. Характерным примером этого случая является задача о назначениях (приводится в качестве примера задачи дискретной оптимизации и для иллюстрации механизма учета в Excel булевости переменных).
Задача. Организация арендует баржу грузоподъёмностью 200 т. На этой барже предполагается перевозить груз 4 типов. Вес и стоимость единицы груза соответственно равны 20, 15, 20, 14 и 100, 80, 40, 30. Необходимо погрузить на баржу груз максимальной стоимости.
Экономико-математическая модель:
Введём необходимые обозначения: пусть xj (j=1,2,3,4) – число предметов j-го типа, которое следует погрузить на баржу. Тогда ЭММ задачи о подборе для баржи допустимого груза максимальной стоимости запишется следующим образом:
max f(x1, x2, x3, x4) =100x1+80x2+40x3+30x4, 20x1+15x2+20x3+14x4 ≤ 200, xj (j=1, 2, 3, 4) – целые неотрицательные.
Решение.
Необходимо последовательно выполнить следующие операции:
1. Создать текстовую форму-таблицу для ввода условий задачи и ввести исходные данные:
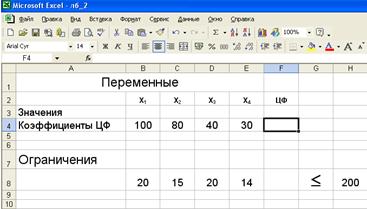
2. Ввести зависимость для целевой функции:
· курсор в ячейку F4;
· кнопка Мастер функции;
· на экране появится диалоговое окно Мастер функций – шаг 1 из 2.
· выбрать на категорию Математические;
· выбрать функцию СУММПРОИЗВ;
· в строку Массив 1 ввести B$3:E$3;
· в строку Массив 2 ввести B4:E4;
· кнопка ОК.
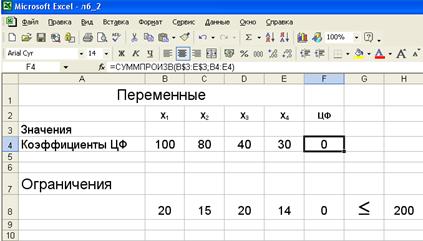
3. Ввести зависимость для ограничений:
· скопировать полученную формулу в ячейку F8.
В строке Меню указатель мыши на Сервис. В развёрнутом меню команда Поиск решения. Появляется диалоговое окно Поиск решения.
4. Назначим целевую функцию (установим целевую ячейку):
· курсор в строку Установить целевую ячейку;
· введем адрес ячейки $F$4;
· введем направление целевой функции в зависимости от условия задачи – Максимальному значению;
· курсор в строку Изменяя ячейки;
· введем адреса искомых переменных $B$3:$E$3.
5. Введите ограничения:
· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;
· в строке Ссылка на ячейку введем (или укажем на листе) адрес $F$8;
· выберем знак ограничения <=;
· в строке Ограничение введем адрес $H$8;
· кнопка Добавить
· в строке Ссылка на ячейку введем (или укажем на листе) адрес $B$3:$E$3;
· выберем значение цел
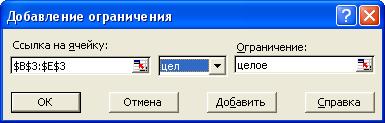
· кнопка ОК.
На экране появится диалоговое окно Поиск решения с введёнными условиями.
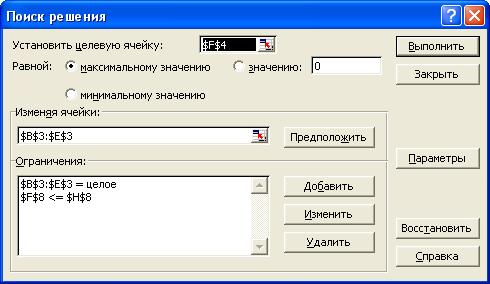
6. Введем параметры для решения задачи:
· кнопка Параметры.
· на экране диалоговое окно Параметры поиска решения;
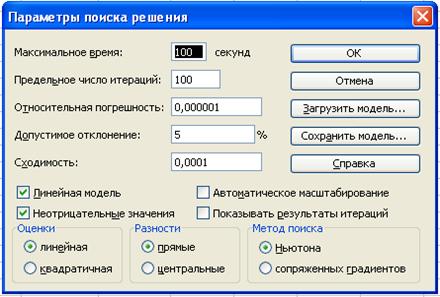
· установим флажки:
ü Линейная модель (это обеспечит применение симплекс-метода)
ü Неотрицательные значения;
· кнопка ОК.
· на экране появится диалоговое окно Поиск решения;
· кнопка Выполнить.
Появится диалоговое окно Результаты поиска решения.
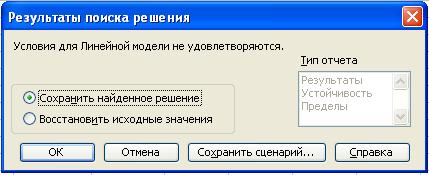
· выберем Сохранить найденное решение
· кнопка ОК.
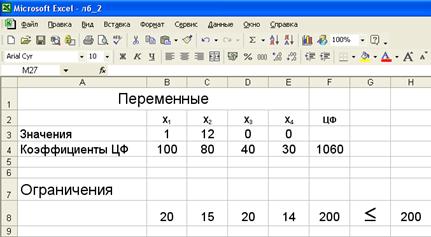
Таким образом, рекомендуемое управленческое решение с позиций принятого критерия оптимизации – следует погрузить 1 предмет первого типа и 12 предметов второго типа. В этом случае стоимость груза составит 1060 у. е., и грузоподъёмность будет использована полностью.
Задачи для самостоятельного решения
1. Задача об оптимальном использовании ограниченных ресурсов. На участок строящейся дороги необходимо вывезти 20 000 м3 каменных материалов. В районе строительства имеются три карьера с запасами 8000м3, 9000 м3 и 10000 м3. Для погрузки материалов используются экскаваторы, имеющие производительность 250 м3/смену в карьерах А, Б и 500 м3/смену в карьере В. Эти карьеры обеспечивают каменными материалами также ряд других строящихся объектов. На погрузку материалов для рассматриваемого участка выделен для экскаваторов общий лимит 60 машино/смен с правом использовать его по усмотрению строителей. Транспортные затраты на перевозку материалов характеризуются следующими показателями: на перевозку 1000 м3 материалов из карьера А требуется 100 машино/смен, из карьера Б – 135 машино/смен, из карьера B – 170 машино/смен.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Основные порталы (построено редакторами)