В Ехсеl признаком достижения оптимума является величина относительного приращения ЦФ на каждой итерации
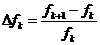
Оптимум считается достигнутым, если выполняется условие Δfk ≤ Δfзад, где Δfзад – точность, назначаемая при решении задачи в режиме Параметры.
Примером задачи НЛП является модель оптимального формирования портфеля ценных бумаг (модель Марковица минимального риска).
В этой модели приняты следующие обозначения (j= 1,…, п):
xj – доля капитала, потраченная на покупку ценных бумагу j-го вида (весь выделенный капитал принимается за 1);
mj – средняя ожидаемая доходность (эффективностью) j-й ценной бумаги;
vj – дисперсия случайной доходности j-й ценной бумаги;
rj = ![]() – называют риском j-й ценной бумаги.
– называют риском j-й ценной бумаги.
В предположении о некоррелированности ценных бумаг (их независимости) модель Марковица имеет вид:
Найти xj, минимизирующие риск портфеля ценных бумаг
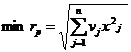
при условии, что обеcпечиваетcя заданное значение эффективности портфеля тр, т. е.
![]()
и условии, что весь выделенный для инвестиций капитал в целых моделирования принимается за 1, т. е.
![]() xj ≥0, j= 1,…,п
xj ≥0, j= 1,…,п
В модели нелинейной является целевая функция.
Рассмотрим некоторые типовые задачи (модели) нелинейной оптимизации.
Задача. Необходимо сформировать оптимальный портфель Марковица (минимального риска) трех ценных бумаг с эффективностями и рисками: (4,10), (10,40), (40,80). Нижняя граница доходности портфеля задана равной 15.
Экономико-математическая модель
Пусть xj, j= 1,2,3 – доля капитала, потраченная на покупку ценных бумагу j-го вида (весь выделенный капитал принимается за 1)
![]()
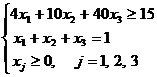
Решение.
Приведенная ЭММ является моделью задачи нелинейного программирования. Специальный (рабочий) лист может быть подготовлен в виде:
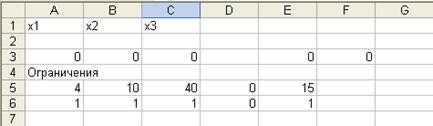
формулы этого листа приведены в ячейках.
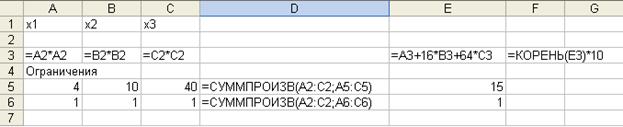
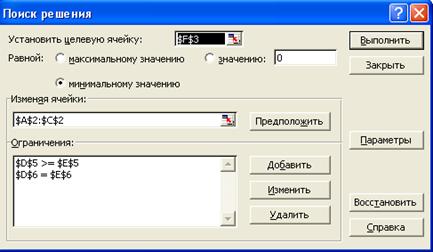
Диалоговое окно Поиск решения с введенными ограничениями, соответствующее приведенному выше рабочему листу:
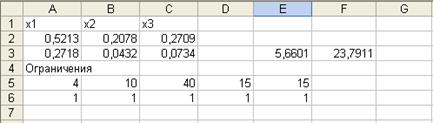
Реализуя приведенную модель средствами MS Excel, будем иметь оптимальный портфель Марковица:
х1 = 0,5213, х2 = 0,2078, х3 = 0,2709,
т. е. доли ценных бумаг оказались равными 52,13%; 20,78% и 27,09%. При этом минимальный риск – 23,79, доходность портфеля оказалась равной заданной – 15.
Задачи для самостоятельного решения
1. Предприятие располагает двумя способами производства данного вида продукции. В течение рассматриваемого периода времени необходимый объем продукции равен 100= Х1 + Х2, где Х1 и Х2 – объемы производства по соответствующему технологическому способу. Затраты производства S при каждом способе зависят от объемов нелинейно:
, .
Необходимо так распределить объем производства между технологическими способами, чтобы минимизировать общие затраты производства.
2. Необходимо сформировать оптимальный портфель Марковица (минимального риска) трех ценных бумаг с эффективностями и рисками: (6,10), (10,50), (60,80). Нижняя граница доходности портфеля задана равной 20.
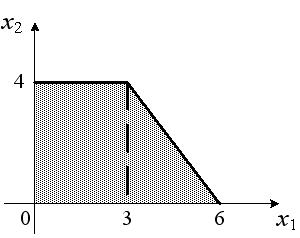
3. Найдите минимум функции ![]() при ограничениях
при ограничениях
![]()
Решите данную задачу методом кусочно-линейной аппроксимации.
4. Найдите максимум функции ![]() при ограничениях
при ограничениях
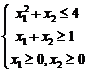
4. Контрольные тесты
для проверки знаний и степени усвоения учебного материала по курсу «Методы оптимальных решений»
1. Организация арендует баржу грузоподъемностью 83 т, на которой предполагает перевозить груз, состоящий из предметов четырех типов. Веса и стоимости предметов равны соответственно 24 т, 22 т, 16 т, 10 т и 96у. е., 85у. е., 50у. е., 20у. е. Требуется погрузить на баржу груз максимальной стоимости, которая равна
1*. 308 у. е.
2. 300 у. е.
3. 200 у. е.
4. 392 у. е.
5. 256 у. е.
Уровень сложности –2, время – 1300 с
2. Найти максимальное значение функции F=2x1+3x2 при ограничениях
x1+3x2 ≤18, 2x1+x2 ≤16, x2 ≤5, 3x1 ≤21, x1≥0, x2≥0
1. 20
2*. 24
3. 21
4. 18
5. 28
Уровень сложности – 1, время – 1200 с
3. Найти минимальное значение функции F=4x1+6x2 при ограничениях
3x1+x2 ≥9, x1+2x2 ≥8, x1+6x2 ≥12, x1≥0, x2≥0
1*. 26
2. 24
3. 22
4. 20
5. 28
Уровень сложности – 1, время – 1200 с
4. Определите минимальную стоимость перевозки грузов
Мощности | Мощности потребителей | |||
поставщиков | 22 | 34 | 41 | 20 |
31 | 10 | 7 | 6 | 8 |
48 | 5 | 6 | 5 | 4 |
38 | 8 | 7 | 6 | 7 |
1*. 668 условных денежных единиц
2. 1200 условных денежных единиц
3. 508 условных денежных единиц
4. 560 условных денежных единиц
5. 290 условных денежных единиц
Уровень сложности – 2, время – 1700 с
5.
Работники | Производительность труда работников по должностям | |||
А1 | 9 | 6 | 5 | 8 |
А2 | 4 | 8 | 6 | 2 |
А3 | 6 | 7 | 9 | 4 |
А4 | 2 | 7 | 3 | 1 |
Максимум производительности труда равен
1*. 28 условных единиц
2. 33 условные единицы
3. 42 условные единицы
4. 54 условные единицы
5. 67 условных единиц
Уровень сложности – 3, время – 1900 с
6. ( - выберите один вариант ответа) | ||||||||||
ВАРИАНТЫ ОТВЕТОВ:
| ||||||||||
7. ( - выберите один вариант ответа) | ||||||||||
ВАРИАНТЫ ОТВЕТОВ:
| ||||||||||
8. ( - введите ответ) | |
ВАРИАНТЫ ОТВЕТОВ: | |
9( - выберите один вариант ответа) | ||||||||||
ВАРИАНТЫ ОТВЕТОВ:
| ||||||||||
10. ( - выберите один вариант ответа) | ||||||||||
ВАРИАНТЫ ОТВЕТОВ:
| ||||||||||
11. ( - выберите один вариант ответа) | |||||||||||||
ВАРИАНТЫ ОТВЕТОВ:
| |||||||||||||
|
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЧЕТУ

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
 Основные порталы (построено редакторами)
Основные порталы (построено редакторами)

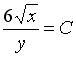
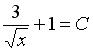
 и предложения
и предложения 