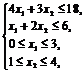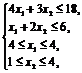IV этап. Решаем задачу 4 симплексным методом. Получим Zmax = 12 при 
= (4; 0; 2; 2; 0; 0). Задачу исключаем из списка, но при этом меняем Z0; Z0= Z()=12, ибо план целочисленный.
V этап. Решаем задачу 5 симплексным методом. Получим Zmax = 12,25 при 
=(3,75; 1; 0; 0,25; 0,25; 0; 3). Z0 не меняется, т. е. Z0=12, ибо план нецелочисленный. Так как 
- дробное, из области решений исключаем полосу 3<x1<4 и задача 5 разбивается на две задачи: 6 и 7.
Задача 6 | Задача 7 |
Z = 3x1 + x2 ® max при ограничениях:
х1, х2 – целые числа. | Z = 3x1 + x2 ® max при ограничениях:
х1, х2 – целые числа. |
Список задач: 6 и 7. Значение Z0=12.
VI этап. Решаем одну из задач списка, например задачу 7, симплексным методом.
Получим, что условия задачи 7 противоречивы.
VII этап. Решаем задачу 6 симплексным методом. Получим Zmax = 10,5 при 
=(3; 1,5; 1,5; 0; 0; 0,5; 2,5). Так как Z()=10,5 < Z0=12, то задача исключается из списка.
Итак, список задач исчерпан и оптимальным целочисленным решением исходной задачи будет Х* = = (4; 0; 2; 2; 0; 0), а оптимум линейной функции Zmax =12.
3. Транспортная задача
Классическая транспортная задача
В исследовании операций под транспортной задачей обычно понимают задачу выбора плана перевозок некоторого товара (изделий, груза) от m источников (пунктов производства, поставщиков) к n стокам, (станциям назначения, пунктам сбыта), обеспечивающего минимальные транспортные затраты. При этом предполагают, что: а) мощность i-го источника (объем поставок товара от i-го источника) равна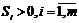
; б) мощность j-го стока (объем поставок товара к j - му стоку) равна
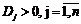; в) стоимость перевозки единицы товара (в условных денежных единицах) от i-го источника к j-му стоку равна сij; г) суммарная мощность всех источников равна суммарной мощности всех стоков (условие закрытости транспортной задачи), т. е.
(1)
Считаем 
.
Для математического описания транспортной задачи вводят переменные xij, обозначающие объемы поставок товара от i-го источника к j-му стоку. В этом случае xi1+xi2+…+xin— общий объем поставок товара от i-го источника, т. е. мощность этого источника; x1j+x2j+…+xmj — общий объем поставок товара к j-му стоку, т. е. мощность этого стока;
c11x11+c12x12+…+cmnxmn-суммарная стоимость перевозок товара от источников к стокам. С учетом этого рассматриваемая задача может быть представлена в следующем виде:
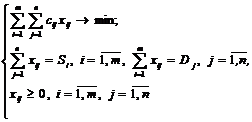(2)
Таким образом, классическую транспортную задачу (1)-(2) можно представить в виде так называемой транспортной таблицы (табл. 1).
Таблица.1
Пункт производства | Пункт потребителя | |||||
1 | … | j | … | n | Поставки | |
1 … i … m | x11/ c11 … xi1/ ci1 … xm1/ сm1 | … … … … … | x1j /c1j … xij /cij … xmj /сmj | … … … … … | x1n /c1n … xin/ cin … xmn /сmn | S1 … Si … Sm |
Спрос | D1 | … | Dj | … | Dn |
Симплексный метод решения задач транспортного типа (метод потенциалов)
Любое допустимое базисное решение классической транспортной задачи будет содержать n + m— 1 базисных переменных.
Легко показать, что задача линейного программирования, двойственная классической транспортной задаче состоит в максимизации целевой функции
(3)
при ограничениях
(4)
где переменные ui, 
, и vj, 
, не ограничены в знаке (будем называть их потенциалами).
Начнем с нахождения начального базисного решения для рассматриваемой классической транспортной задачи, воспользовавшись ее транспортной таблицей (см. табл.1) и так называемым правилом северо-западного угла.
Следуя правилу северо-западного угла, полагаем 
Если x11=S1, то выделяем первую строку транспортной таблицы (возможности первого источника полностью исчерпаны и 
) и заменяем d1 на D1-S1. Полученная транспортная таблица соответствует классической транспортной задаче c m-1 источником и n стоками. Следовательно, процедуру нахождения начального базисного решения можно повторить, определив значение переменного модели x21 расположенного в северо-западном углу новой транспортной таблицы, и т. д.
Понятно, что если x11 = D1, то нужно выделить первый столбец транспортной таблицы (возможности первого стока полностью исчерпаны и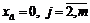 
) и заменить S1 на S1 — D1. В этом случае полученная транспортная таблица соответствует классической транспортной задаче с m источниками и n-1 стоками, а в ее северо-западном углу расположено переменное модели x12.
Если S1 = D1, то можно выделить либо только первую строку исходной транспортной таблицы, либо только ее первый столбец. Так, если выделить первую строку, то S1 + D1= 0 и на следующем шаге переменное модели х21 становится базисным и принимает нулевое значение. Поэтому на втором шаге выделяем первый столбец. Если сначала выделить первый столбец, то S1 - D1= 0, на следующем шаге переменное модели х12 становится базисным и принимает нулевое значение. Поэтому на втором шаге выделяем первую строку.
Задача 1. Пусть классическая транспортная задача, для которой необходимо найти начальное базисное решение представлена своей транспортной таблицей (табл. 2). В эту таблицу включены только значения сij, i=1,2,3, 
. В процессе нахождения начального базисного решения в транспортной таблице будем проставлять значения только базисных переменных. Это позволит различать нулевые значения базисных переменных начального решения и значения свободных переменных, которые равны нулю всегда.
Таблица 2
Источник | Сток | Поставки | |||
1 | 2 | 3 | 4 | ||
1 2 3 | с11 с21 с31 | с12 с22 с32 | с13 с23 с33 | с14 с24 с34 | 10 5 15 |
Спрос | 5 | 10 | 8 | 7 |
|
В данном случае 10 = S1> D1= 5. Поэтому по правилу северо-западного угла полагаем x11=D1=5, в табл.2 выделяем первый столбец, фиксируя тем самым, что все остальные переменные этого столбца (x21 и x31) являются свободными и, как следствие, равными нулю. Проставляя x11 = 5 и заменяя S1 на S1 – D1, приходим к табл.3
Таблица 3
Источник | Сток | Поставки | |||
1 | 2 | 3 | 4 | ||
1 2 3 | 5 / с11 с21 с31 | с12 с22 с32 | с13 с23 с33 | с14 с24 с34 | 5=10-5 5 15 |
Спрос | 0=5-5 | 10 | 8 | 7 |
|
В северо-западном углу незаштрихованной части табл. 3 находится переменное х12 и 10 = D2>S1= 5. Поэтому полагаем x12= S1= 5, в табл. 8 заштриховываем первую строку и после замены D2 на D2 –D1 = 5 приходим к табл.4
Таблица 4
Источник | Сток | Поставки | |||
1 | 2 | 3 | 4 | ||
1 2 3 | 5/с11 с21 с31 | 5 /с12 | с13 | с14 | 0=5-5 |
с22 с32 | с23 с33 | с24 с34 | 5 15 | ||
Спрос | 0 | 5=10-5 | 8 | 7 |
|
В северо-западном углу незаштрихованной части табл. 4 находится переменное x22 и S2=5=D2. Таким образом, можно найти два начальных базисных решения, в первом из которых x22=D2 = 5 и заштриховывается второй столбец в табл. 4, а во втором x22=S2=5 и в табл. 4 заштриховывается вторая строка. Воспользуемся первым из возможных вариантов и, заменив S2 на S2-D2, приходим к табл. 5
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Основные порталы (построено редакторами)