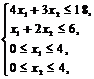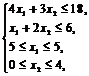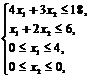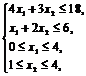Фонд оценочных средств по направлению подготовки (специальности)38.03.01 Экономика направленность (профиль/специализация) «Общий » (стр. 5 )

которое приводим к виду

(8’’)

С помощью дополнительной переменной x7³0 приводим это неравенство к равносильному уравнению, которое включаем в систему ограничений, полученную на последнем, 5 шаге, решения расширенной задачи (1’’)-(3’’), (6’’) симплексным методом. Имеем:

6 шаг. Основные переменные x1, x2, x3, x7; неосновные переменные x4, x5; x6.

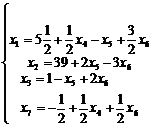
Опуская дальнейшее решение задачи симплексным методом (предлагаем выполнить самостоятельно), получим на заключительном, 7 шаге:

7 шаг. Основные переменные x1, x2, x3, x4; неосновные переменные x5; x6, x7.

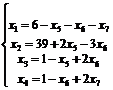
z=46+ x7, т. е. z7=46 при X7 (6;39;1;1;0;0;0).

Так как в выражении линейной функции нет неосновных переменных с отрицательными коэффициентами, то x7 – оптимальное целочисленное решение исходной задачи.

Следует обратить внимание на то, что в полученном выражении линейной функции z отсутствуют неосновные переменные x5 и x6. Это означает, что, вообще говоря, существует бесконечное множество оптимальных решений (любых, не обязательно целочисленных), при которых 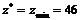. Эти решения получаются при значении неосновной переменной x7 (входящей в выражение для z), равной нулю, т. е. при x7=0, и при любых значениях неосновных переменных x5 и x6, (не входящих в выражение для z), которое «позволяет» принять система ограничений:

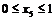и , т. е. при и .

Но в силу условия целочисленности, переменные x5 и x6 могут принять только значения 0 или 1. Поэтому задача будет иметь 4 целочисленных оптимальных решения, когда x5 и x6 в любой комбинации принимают значения 0 или 1 , а x7 =0. Подставляя эти значения в систему ограничений на 7 шаге, найдем эти оптимальные решения: X(6;39;1;1;0;0;0), X(7;36;3;0;0;1;0), X(5;41;0;1;1;0;0), X(6;38;2;0;1;1;0).

Наличие альтернативных оптимальных целочисленных решений позволяет осуществить выбор одного из них, руководствуясь дополнительными критериями, не учитываемыми в математической модели задачи. Например, из условия данной задачи следует, что распиливание бревен не дает отходов лишь по второму способу, поэтому естественно при выборе одного из четырех оптимальных решений отдать предпочтение решению X, при котором максимальное число бревен (x2=41) распиливается без отходов.

Итак, при оптимальных целочисленных решениях (5;41;0), (6;39;1), (7;36;3), (6;38;2). (При записи оптимальных решений мы оставили лишь первые три компоненты, выражающие число бревен, распиливаемых соответственно 1-м, 2-м и 3-м способами, и исключили последние 4 компоненты, не имеющие смыслового значения).

Недостатком метода Гомори является требование целочисленности всех переменных – как основных (выражающих, например, в задаче об использовании ресурсов единицы продукции), так и дополнительных переменных (выражающих величину неиспользованных ресурсов, которые могут быть и дробными).

Остановимся на комбинаторных методах решения задач целочисленного линейного программирования.

Метод ветвей и границ

Его суть заключается в упорядоченном переборе вариантов и рассмотрении лишь тех из них, которые оказываются по определенным признакам перспективными, и отбрасывании бесперспективных вариантов.

Метод ветвей и границ состоит в следующем: множество допустимых решений (планов) некоторым способом разбивается на подмножества, каждое из которых этим же способом снова разбивается на подмножества. Процесс продолжается до тех пор, пока не получено оптимальное целочисленное решение исходной задачи.

Пусть ЗЛП решена симплексным методом и известны нижняя и верхняя границы для каждой целочисленной переменной xj:vj£xj£wj (j=1, 2, ..., n), а также нижняя граница линейной функции Z0, т. е. при любом плане Х Z(X) ³Z0. Предположим для определенности, что только первая компонента оптимального плана Х* ЗЛП не удовлетворяет условию целочисленности. Тогда из области допустимых решений задачи исключается область: []<<[]+1, где []- целая часть числа . В результате из ЗЛП (ЗЛП1) формируют две задачи: 2 и 3, отличающиеся друг от друга тем, что в задаче 2 кроме ограничений (2) задачи 1 добавлено ограничение []+1££w1. Получим список из двух задач: 2 и 3.

Решаем одну из них (любом порядке). В зависимости от полученного решения список задач расширяется, либо уменьшается.

Если в результате решения одной из задач 2 или 3 получен не целочисленный оптимальный план, для которого Z(X*)£Z0, то данная задача исключается из списка. Если Z(X*)>Z0, то из данной задачи формируются новые две задачи. Если полученной решение Х* удовлетворяет условию целочисленности и Z(X*)>Z0, то значение Z0 исправляется и за величину Z0 принимается оптимум линейной функции полученного оптимального целочисленного плана.

Процесс продолжается до тех пор, пока список задач не будет исчерпан, т. е. задачи не будут решены.

Проиллюстрируем метод ветвей и границ на примере.

Задача. Решить задачу Z = 3x1 + x2 ® max при ограничениях:

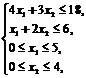
х1, х2 – целые числа.

Решение. За нижнюю границу линейной функции примем, например, ее значение в точке (0,0), т. е. Z0= Z(0; 0) = 0.

I этап. Решая задачу симплексным методом, получим Zmax=13 при = (4,5; 0; 0; 1,5; 0,5; 4); так как первая компонента дробная, то из области решения исключается полоса, содержащая дробное оптимальное значение , т. е. 4<x1<5. Поэтому задача 1 разбивается на две задачи 2 и 3:

Задача 2

Задача 3

Z = 3x1 + x2 ® max при ограничениях:

х1, х2 – целые числа.

Z = 3x1 + x2 ® max при ограничениях:

х1, х2 – целые числа.

Список задач: 2 и 3. Нижняя граница линейной функции не изменилась: Z0=0.

II этап. Решаем (по выбору) одну из задач списка, например задачу 3 симплексным методом.

Получим, что условия задачи 3 противоречивы.

III этап. Решаем задачу 2 симплексным методом. Получим при . Хотя , по-прежнему сохраняется Z0=0, ибо план Х3 нецелочисленный. Так как - дробное число, из области решений исключаем полосу 0<x2<1 и задачу 2 разбиваем на две задачи 4 и 5.