Социально-экономическое прогнозирование (стр. 8 )

Принцип «дерева» наиболее полно соответствует реальной сис­теме как социальных проблем, так и социальных целей, какими они предстают в социальной действительности, где что-то является клю­чевым (для проблем) или конечным (для целей), а остальное – про­изводным различных порядков от ключевого или конечного.

В идеале оба «дерева» должны обеспечивать дезагрегацию про­блем и целей на все более детальные составляющие предыдущего уровня, получение производных различных порядков, логически вытекающих одна из другой, и выявление существенно новых про­блем или соответственно – достижение уже выявленных.

Теоретический инструмент исследования проблемно-целевых ситуаций можно представить в виде «проблемно-целевого ромба», вершины которого составляют конечная цель (самоцель) – с одной стороны, и ключевая (основополагающая) проблема – с другой, а оба ребра на разных уровнях соответствуют целям и проблемам различных порядков.

Линия соприкосновения идет по самому нижнему, самому конкретному, детализированному, дезагрегированному уровню каж­дого «дерева» где достижение какой-то частной, конкретной цели подразумевает решение соответствующей частной, конкретной про­блемы. Но дальше логика построения того и другого «дерева» при­обретает своеобразие, «Дерево целей» строится как бы «сверху вниз»: определяется конечная цель и самоцель системы, затем – производные от нее цели второго порядка, без достижения которых невозможно достичь конечной, затем – производные цели третье­го и последующих порядков, обусловливающие достижение преды­дущих, и т. д., вплоть до нижнего, максимально конкретизированно­го, дезагрегированного уровня. «Дерево проблем» логически начи­нается именно с последнего.

Графически это можно изобразить в виде проблемно-целевого ромба, ориентирующего исследователя на комплексный подход к изучению целей и проблем всех порядков как единой иерар­хической системы.

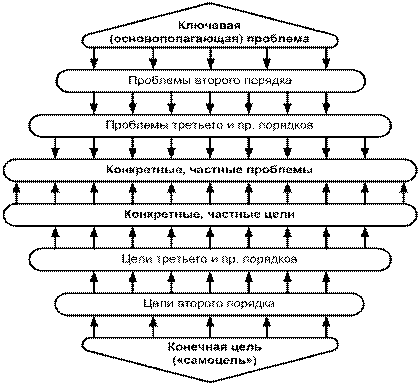
Рисунок 4. Проблемно-целевой ромб

Наиболее сложным вопросом является ранжирование целей и проблем в рамках одного уровня, которое позволяет определить собственно основные направления развития и последовательность (приоритетность) достижения целей и решения задач в их рамках. Часто такая оценка проводится экспертным путем, что не исключает использование количественных (например, статистических) методик в процессе сбора и анализа оценок экспертов.

В качестве пример количественной методики анализа экспертных оценок в процессе ранжирования целей можно привести следующий алгоритм.

1.  Создание рабочей группы (назначение ответственного) по проведению экспертизы.

2.  Формирование группы опрашиваемых экспертов (от 10 до 200).

3.  Оценка репрезентативности (от фр. выбранной группы (как среднего арифметического компетентности участников группы). Компетентность определяется по коэффициентам осведомленности (уровень знаний по проблеме, оценка составляется отдельно для каждого эксперта, алгоритм расчетов должен учитывать квалификационные характеристики экспертов, важные для проводимой экспертизы) и аргументированности (структура аргументов, лежащих в основании оценки):

,

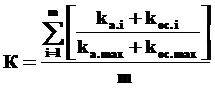где ka.i и koc.i – коэффициенты аргументированности и осведомленности мнения i-го эксперта (max – максимальные значения коэффициентов по совокупности экспертов), m – общее число экспертов. Группу можно считать репрезентативной, если К в интервале от 0, 67 до 1.

Таблица 2. Возможная шкала определения коэффициента аргументированности мнения эксперта

4.  Составляется анкета экспертной оценки и вопросов, предлагаемых экспертам (указание цели опроса; формулировка генеральной цели, проблемы; перечень подцелей, подпроблем; определение перечня средств достижения цели)

5.  Сбор мнений экспертов.

6.  Обработка результатов

·  средняя оценка значимости цели по направлениям. Значимость цели определяется как простая арифметическая средняя из оценок ее значимости всеми экспертами;

·  оценка относительной значимости (путем простого нормирования): значимость данной цели делят на сумму значимостей всех целей ее уровня, необходимых для достижения связанной с ней цели более высокого уровня);

·  оценка относительной важности цели среди всех целей ее уровня, входящих в дерево, а также, отчасти, по отношению к остальным целям, не включенным в одну с ней вертикальную цепочку (произведение относительных значимостей данной подцели и следующей за ней цели более высокого уровня). Чем больше значение – тем, предположительно, приоритетнее цель.

Допустимо воспользоваться следующей шкалой оценок относительной важности целей.

Таблица 3. Шкала оценки относительной важности целей

Для оценки степени согласованности мнений экспертов можно использовать коэффициент вариации оценок.

Помимо ранжирования целей (проблем) в рамках общей совокупности дерева целей (проблем) охарактеризованная выше методика может применяться в любой ситуации, требующей расстановки приоритетов, оценки важности (анализ альтернатив, распределение ресурсов и т. д.).

2.2. Опросные и групповые экспертные методы

2.2.1. Интервью

Интервью – это целенаправленная беседа (дискуссия) между двумя или более (интервью в фокус-группе) людьми, одним из которых является исследователь, а остальные выступают в качестве источника информации. Понятие «интервью» может означать разные типы сбора данных, тип интервью должен четко соответствовать цели исследования и «исследовательской стратегии»[26].

Интервью могут быть формализованными и структурированными с отдельным набором вопросов для каждого интервьюируемого и неструктурированными, то есть в форме обычной беседы. Между этими крайними полюсами находятся все типы интервью, имеющие в той или иной степени признаки как первой из названных разновидностей, так и второй.

Структурированные интервью являются стандартизированными и проводятся с использованием анкет, содержащих заранее составленные и идентичные для всех участников вопросы. Полученные результаты заносятся в стандартную форму в виде заранее оговоренных кодов. Поскольку возможны отклонения при ответе на вопросы даже в одинаковой формулировке (например, при разъяснении смысла вопроса), интервьюер, чтобы исключить возможность собственной предвзятости, должен озвучивать вопросы одним и тем же тоном и пр.

Частично структурированные и неструктурированные интервью являются нестандартизированными. При проведении частично структурированного интервью требуется список тем для обсуждения или вопросов, на которые желательно получить ответ, причем в процессе собеседования возможны изменения, и не только формулировки. Например, в зависимости от места проведения интервью ли личности интервьюируемого, некоторые вопросы возможно «опускать»., можно менять порядок вопросов. Возможна и формулировка в ходе беседы новых вопросов по мере необходимости. Такая форма ведения интервью предполагает запись (стенографирование, фиксация тезисов, диктофон).

Неструктурированные интервью всегда неформальны. Обычно их проводят, когда требуется глубоко изучить область исследования. Поэтому их часто называют глубинными интервью. Исследователь, как правило, не имеет какого-либо заранее составленного перечня вопросов, но должен четко представлять проблему, которая требует изучения. Во время интервью участнику предоставлена возможность свободного обсуждения любых событий, моделей поведения, точек зрения, связанных с темой исследования. Отсюда такой тип взаимодействия интервьюера и участника часто называют недирективным, а само интервью – информантным, поскольку его направление во многом определяет интервьюируемый. В отличие от информантного интервью респондентное интервью полностью «ведет» исследователь, а участник только отвечает на четко сформулированные вопросы.

Метод «аналитической записки» (аналитическая экспертная оценка) отчасти схож с заочным интервью. Он предполагает длительную и тщательную самостоятельную работу эксперта, связанную с анализом тенденций, оценкой состояния и путей развития объекта прогнозирования. Это дает эксперту полную свободу в использовании любой необходимой и доступной ему информации об объекте прогнозирования. Свои соображения эксперт оформляет в виде докладной записки в соответствии с заданной или в произвольной форме.

2.2.2. Мозговой штурм

«Мозговой штурм» или «мозговая атака» (от англ. Brainstorming) ценен именно как метод генерации идей и вариантов развития событий: он дает количество разнообразных идей в 2 – 4 раза больше, чем тогда, когда эксперт принимает решение один. Для того чтобы применение мозгового штурма было эффективным, необходимы знания его специфики.

Использование этого метода вызвано тем, что:

ü  при обычном обсуждении проблем возникновению новаторских идей препят­ствуют контролируемые механизмы сознания;

ü  поток идей сковывается под давлением стереотипных форм принятия реше­ний;

ü  оригинальные идеи рождаются в процессе побуждения к свободным ассоциа­циям.

Мозговой штурм обычно проходит в два этапа:

1.  генерация идей группы экспертов и их звукозапись и/или стенографирование (максимальная продолжительность – 45 минут).

2.  оценка идей путем прослушивания/просмотра записей и группировки мне­ний.

Основной принцип проведения мозгового штурма – отсутствие критики, разде­ление этапа генерации и оценки идей. Размер группы должен быть около 8 – 15 чело­век плюс модератор (ведущий) (большее количество, обычно, неэффективно, слабоуправляемо, может вызвать хаос). Не­обходимым условием использования метода является создание неформальной атмо­сферы, раскрепощение участников. Однако сложно создать такие условия в деловой обстановке, кроме того метод не исключает появления абсурдных идей, ухода от проблемы.

Для применения метода, таким образом, важное значение имеет «квалификация» ведущего, задачами которого являются создание и поддержание обстановки свободы выражения мыслей и безусловного внимания к инициативе каждого (возможно – побуждение к участию), недопущение проявления «лидеров мнения», «заглушающих» других участников, пресечение критики на этапе генерации идей, обеспечение фиксации всех поступивших предложений ото всех участников, отслеживание ситуации «ухода от проблемы».

Основным недостатком разовых опросов экспертов, как и дискуссии, является низкая их эффективность (в смысле соотношения затрачиваемых усилий и полезного результата). Это вызвало разработку заочного варианта «метода соотнесенной оценки», получившего название методика «Дельфи» или «дельфийская техника».

2.2.3. Метод Дельфи

Метод Дельфи в своей основе содержит идею о потенциальной возможности самообучения экспертов при проведении заочного опроса в несколько туров. Гарантируется соблюдение анонимности респондента (во избежание «давления авторитетов» и опасения за свою репутацию в случае неожиданных ответов). Респондентам предоставляется возможность знакомиться с материалами предыдущего тура и последовательно уточнять свои оценки по мере изучения новых аргументов.

Процедура опроса экспертов по методике «Дельфи» заключается в анкетировании экспертов с помощью опросных листов, или внешних устройств ЭВМ в несколько туров с обработкой результатов в каждом туре и информированием экспертов об этих результатах. На практике обычно ограничиваются четырьмя турами.

В первом туре опроса эксперты дают свои ответы без аргументирования. Ответы обрабатываются с целью выделения среднего и крайних мнений, экспертам сообщаются эти мнения. Во втором туре опроса они пересматривают и при желании изменяют ответы, данные в первом туре.

Кроме того, эксперты должны объяснить, почему они изменили или не изменили свои ответы. Полученные после второго тура новые средние и крайние мнения, а также вся аргументация с сохранением анонимности сообщается экспертам и проводится третий тур опроса, в ходе которого эксперты снова пересматривают ответы и аргументируют свое решение. Последующие туры аналогичны.

Как правило, после третьего или четвертого туров опроса ответы экспертов перестают изменяться, что и является сигналом к прекращению опросов. Такая процедура позволяет экспертам учесть обстоятельства, которыми они пренебрегли, или о которых не были осведомлены. По решению ведущего опрос обоснование могут предоставлять лишь эксперты, мнения которых сильно отличаются от мнения большинства.

Необходимость обоснования мнений вынуждает тех экспертов, у которых нет твердого убеждения в собственной правоте, помещать свои ответы вблизи от среднего мнения. В то же время эксперты, которые смогли обосновать свои «особые» ответы, несмотря на новую информацию, придерживаются своих первоначальных взглядов.

Иногда образуются две группы экспертов с различными мнениями. Это свидетельствует о наличии двух различных подходов, что может объясняться, например, существованием двух различных научных школ. Дальнейшее проведение опроса в таком случае, как правило, лишь подтверждает создавшееся положение, тогда рассмотрение разных позиций требует глубоких исследований и не может быть результатом экспертизы. Однако и здесь опрос полезен, ибо отчетливо выявляет позиции, точки зрения и их аргументацию, что позволяет вести дальнейшее исследование проблемы.

Распространились и упрощенные вариации «дельфийской техники» («мини-Дельфи»), позволяющие собрать оценки двух-трех туров за несколько дней, или даже часов. Особенно упрощается техника сбора оценок при использовании информационных технологий подключения экспертов к работе. Имеется еще несколько разновидностей заочного опроса экспертов, но все они занимают то, или иное, как бы промежуточное положение между простейшим разовым анкетированием и сложнейшей «дельфийской техникой».

Важно отметить, что экспертиза в области прогнозирования имеет свою специфику и предъявляет особые требования к специалистам, которые определяют перспективы развития общества, отдельных социальных групп, явлений, процессов:

-  во-первых, необходимо быть аналитиком;

-  во-вторых, уметь находить связи и зависимости между процессами и факторами, определяющими их развитие;

-  в-третьих, не только прогнозировать на основе существующих тенденций, но и предвидеть развитие «скачкообразное» с учетом влияния возможных различных факторов (допустим, рыночной экономики: процессов коммерциализации, изменений в сфере услуг, образования, культуры, нравственности и т. д.).

Глава 3. Формализованные математические методы прогнозирования в государственном управлении

3.1. Модели временных рядов

3.1.1.  Понятие временного ряда. Трендовые модели

3.1.2.  Разновидности уравнений временного тренда

3.1.3.  Особенности прогнозирования на основе трендовых моделей

3.2. Эконометрическое моделирование

3.2.1.  Общее понятие эконометрических моделей

3.2.2.  Линейная регрессия. Метод наименьших квадратов

3.2.3.  Отбор переменных эконометрической модели

3.2.4.  Оценка качества параметров и анализ эконометрической модели

3.2.5.  Тестирование выполнения допущений метода наименьших квадратов в модели линейной регрессии

3.2.6.  Прогнозирование на основе эконометрических моделей (на примере модели из одного уравнения)

3.3. Разработка индикаторов

3.4. Метод «затраты-выпуск» и модель межотраслевого баланса

3.4.1.  Общая схема таблицы межотраслевого баланса

3.4.2.  Статическая модель межотраслевого баланса – модель «затраты-выпуск»

3.4.3.  Динамическая модель межотраслевого баланса

Главное отличие описываемой группы методов от названных ранее логико-интуитивных методов – наличие математически формализованного алгоритма работы с изучаемой информацией и однозначно определенная форма результатов применения метода. Основной инструмент построения выводов, таким образом, – не опыт и личностные характеристики экспертов-людей, а формально-определенный логико-математический аппарат, требующий количественной формулировки входной информации.

Подобные особенности формализованных математических методов, с одной стороны, предъявляют более высокие требования к прогнозисту: он должен, как минимум, достаточно хорошо владеть математическим аппаратом метода для корректного и успешного его применения.

Кроме того, математические методы относительно возможностей прогнозирования социально-экономических явления и процессов обладают, как правило, ограничениями, обусловленными самой сущностью применяемого математического аппарата, их применение требует определенных упрощающих допущений относительно анализируемых явлений и процессов. Это сказывается на получаемых результатах: они применимы с известными оговорками. Отсюда, требуется ясно представлять себе характер этих ограничений и то, как они могут влиять на качество получаемого прогноза. Перед прогнозистом стоит проблема выбора метода, адекватного отображаемым явлениям настолько, что полученный с их помощью прогноз будет иметь познавательную и практическую ценность.

С другой стороны, уже существует большое количество разнообразных математических методов изучения социально-экономических (особенно экономических) явлений и процессов, из числа которых можно выбрать тот, которых в наилучшей степени отвечает потребностям исследователя. Ситуация с необходимостью разработки принципиально нового метода (а не приспособления для нужд исследователя уже существующего) встречается сегодня не так часто. И развитие методологии математического анализа социально-экономических явлений продолжается, появляются математические методы анализа и прогнозирования, все более «близкие» сущностно социальным и экономическим объектам.

Практически ценные результаты в процессе прогнозирования при помощи формализованных математических методов могут быть получены исследователем и в отсутствие у него обширных знаний и практического опыта в изучаемой сфере, они будут обусловлены самим алгоритмом метода при его корректном применении. Хотя это не отрицает желательности таких знаний и опыта, они помогают точнее определить корректность применения того или иного метода, провести его «адаптацию» к объекту в случае необходимости.

Среди основных формализованных математических методов и моделей прогнозирования, наиболее часто применяемых в государственном прогнозировании социально-экономического развития можно назвать:

-  модели временных рядов (динамических рядов);

-  статистические индикаторы;

-  эконометрическое моделирование;

-  метод «затраты-выпуск» и модели на его основе.

3.1. Модели временных рядов

3.1.1. Понятие временного ряда. Трендовые модели

Наиболее распространенными формализованными методами прогнозирования являются эстраполяционные, а модели временных рядов – один из наиболее распространенных видов экстраполяционных прогнозных моделей. Временной ряд – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень состояния и изменения изучаемого явления. Уровень временного ряда – значение показателя, динамика которого во времени отображена в виде временного ряда, в рамках ряда.

Временные ряды различаются по следующим признакам.

По времени можно обозначить моментные и интервальные временные ряды. Интервальные временные ряды – последовательности значений, в которых уровни ряда относят к результату накопленному или вновь достигнутому за определенное время (например, объемы производства продукции промышленности по месяцам). Моментный ряд содержит значения показателя на определенный момент времени, на конкретную дату, момент (например, поголовье крупного рогатого скота на начало года). Показатели интервального ряда вполне могут суммироваться. Сумма значений показателей моментного ряда обычно не рассчитывается: часто она не имеет реального содержания и практического смысла.

По форме представления уровней ряда выделяют ряды абсолютных, относительных и средних величин. По расстоянию между датами или интервалами времени – полные и неполные временные ряды. Полные ряды выстроены с равными промежутками между значениями, в неполных принцип равенства периодов времени между уровнями ряда не соблюдается.

По содержанию показателей выделяют ряды частных и агрегированных показателей. Частные показатели характеризуют один конкретный частный признак изучаемого явления. К рядам частных показателей относится, например, временной ряд погодовых значений показателя выпуска студентов ВУЗами страны. Агрегированные показатели основаны на частных и характеризуют изучаемое явление комплексно. Примером агрегированного показателя можно считать индекс инфляции, индекс физического объема производства промышленной продукции.

Обычно прогнозирование на основе временных рядов осуществляется с помощью изучения и экстраполяции временного тренда. Простая трендовая модель динамики на основе временных рядов показателя – это уравнение трен­да с указанием начала отсчета единиц времени. Прогноз по этой модели заключается в подстановке в уравнение тренда номера периода, который прогнозируется.

Определение параметров уравнения тренда может осуществляться практически теми же методами, что и для уравнений регрессионной зависимости, активно используемых в эконометрическом моделировании (парная регрессия), поскольку математически форма уравнений одинакова. Только место факторной переменной занимает фактор «период». Наиболее часто используемый сегодня метод – метод наименьших квадратов (МНК). Нелинейные разновидности уравнений тренда могут быть сведены к линейным, что также позволяет использовать для определения их параметров МНК. Но при этом нужно помнить, что ряд значений показателей времени должен соответствовать типу тренда. Например, для прямолиненого тренда дискретный ряд показателей времени начинается со значения 1 и продолжается по порядку: 2, 3, 4 и т. д. Для иных видов тренда последовательность значений времени может быть и иной (например, для логарифмического уравнения тренда нумерация может начинаться не с 1, а с другой цифры, скажем, 4 или 5, что связано с математическими особенностями логарифмического выражения).

Среди разновидностей моделей на основе временных рядов можно выделить:

1)  Модели собственно тренда:

,

где T(t) – временной тренд заданного вида (например, линейный , εt – стохастическая (случайная) компонента;

2)  Модели сезонности:

,

где S(t) – периодическая (сезонная) компонента, εt - стохастическая (случайная) компонента;

3)  Модели тренда и сезонности:

, аддитивная («дополняющая»),

, мультипликативная («множительная»),

где T(t) – временной тренд заданного вида, S(t) – периодическая (сезонная) компонента, εt – стохастическая (случайная) компонента;

К моделям временных рядов относится множество более сложных моделей, таких, как модели адаптивного прогноза, модели авторегрессии и скользящего среднего (ARIMA) и др. Их общей чертой является объяснение поведения показателя во времени, исходя только из его предыдущих значений. Такие модели могут применяться, например, для прогнозирования объемов производства, объемов продаж, краткосрочного прогноза процентных ставок и т. п.

3.1.2. Разновидности уравнений временного тренда

Далее характеризуются наиболее распространенные и простые математические формы отображения тренда. Их набор вполне достаточен для отображения большинства из встречающихся тенденций временных рядов. При этом желательно из всех возможных уравнений тренда выбирать простейшее, что обусловлено простым правилом: чем сложнее уравнение тренда, тем сложнее гарантировать надежность оценок, тем потенциально выше опасность ошибок.

Самым простым типом линии тренда является прямолинейный тренд, описываемый уравнением первой степени:

,

- выравненные уровни тренда по периодам (моментам) I;

а – свободный член уравнения, численно равный среднему уровню для периода (момента) ti = 0;

b – средняя величина изменения уровня ряда за один период (момент) времени;

ti – номера периодов (моментов) времени, к которым относятся соответствующие уровни временного ряда.

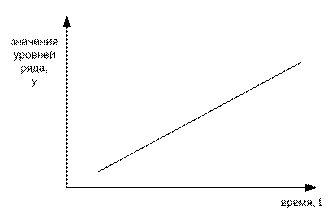
Рисунок 5. Прямолинейный тренд

Этот тип тренда подходит для отображения примерно равномерных пропорциональных изменений уровней ряда. Практика показывает, что такая динамика встречается довольно часто. Знак параметра b показывает направленность изменений: отрицательный знак говорит о тенденции убывания.

Параболический тренд – тенденция, выразимая полиномом (параболой) 2-го порядка:

Полиномы более высоких порядков (3-го и выше) значительно реже применяются для выражения тенденций динамики, поскольку гораздо сложнее с точки зрения получения надежных оценок.

В уравнении тренда а1 – это средний за весь изучаемый период прирост, который изменяется равномерно с ускорением, равным 2 а2. Последнее (ускорение) и служит собственно константой выражения.

Тренд в форме параболы используется для отображения тенденций, которым свойственно примерно постоянное ускорение абсолютных изменений уровней. Такие случаи сравнительно более редки, чем линейные процессы, но, с другой стороны любое отклонение от линейного роста можно интерпретировать как наличие ускорения. Подобными характеристиками могут обладать, например, приросты производства продукции отраслями экономики в фазе циклического подъема экономической конъюнктуры.

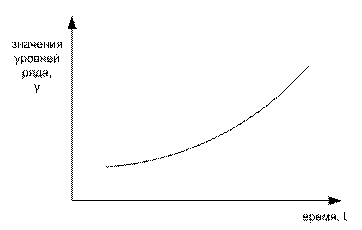
Рисунок 6. Параболический тренд

Относительно статистики, трендом можно обычно считать только одну из ветвей параболы (обычно правую). В более конкретных ситуациях, тем не менее, возможно и объединение обеих ветвей в единый тренд.

Характер тренда определяется знаками а1 и а2 (величина а0 обычно всегда положительна):

–  а1 > 0 и а2 > 0 – восходящий тренд;

–  а1 < 0 и а2 < 0 – нисходящий тренд;<

–  а1 > 0 и а2 < 0 означает либо восходящий тренд с замедляющимся ростом уровней (одна ветвь параболы), либо обе ветви, когда их можно считать одной тенденцией;

–  а1 < 0 и а2 > 0 означает либо нисходящий тренд с замедляющимся ростом уровней (одна ветвь параболы), либо обе ветви, когда их можно считать одной тенденцией;

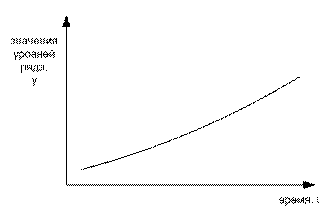
Экспоненциальный тренд характеризуется выражением

или в форме .

Основной параметр k является постоянным цепным темпом изменений уровней. Если k > 1, имеет место тренд с возрастающими уровнями, а равно с возрастающим ускорением роста и возрастающими производными всех более высоких порядков. Если k < 1, имеет место тенденция постоянного, но замедляющегося убывания.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26