Социально-экономическое прогнозирование (стр. 10 )

Как и в случае парной линейной регрессии для анализа статистической значимости полученных оценок коэффициентов множественной линейной регрессии необходимо оценить дисперсию и стандартные отклонения коэффициентов aj.

В общем случае дисперсия коэффициента aj Varaj определяется по формуле:

где Saj – стандартное отклонение величин aj, Zjj – диагональные элементы матрицы (XTX)–1, m – число независимых переменных в модели. Отсюда для проверки гипотезы о величине каждого из коэффициентов рассчитываются, как и в случае парной линейной регрессии, t-статистики коэффициентов:

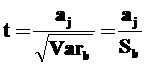
характеризующиеся распределением Стьюдента с n–m–1 степенями свободы.

Доверительные интервалы определяются аналогично случаю с парной регрессией.

Для оценки степени соответствия линии регрессии выборочным данным обычно применяется коэффициент детерминации R²:

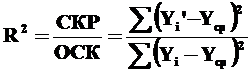
или

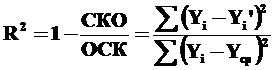
Общая сумма квадратов отклонений (ОСК) – это сумма квадратов разностей между выборочными (наблюдаемыми) значениями зависимой переменной Yi и средней из наблюдений в выборке Yср.:

Сумма квадратов отклонений, объяснимая регрессией (СКР) – это сумма квадратов разностей между прогнозируемыми на основе найденного уравнения регрессии значениями Yi’ и средней из наблюдений в выборке Yср.

Остаточная сумма квадратов (СКО) – это сумма квадратов разностей между выборочными (наблюдаемыми) значениями Yi и рассчитанными на основе найденного уравнения регрессии Yi’.

Коэффициент детерминации принимает значения от 0, когда факторы X не оказывают никакого влияния на зависимую переменную, до 1, когда изменения зависимой переменной Y полностью объяснимы влиянием факторов модели.

Однако в многофакторной регрессии коэффициент детерминации корректируют с учетом числа независимых переменных, рассчитывают скорректированный R² – R²’:

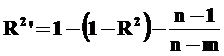
где n – число наблюдений, m – число независимых переменных.

Коэффициент детерминации является R² случайной величиной, поскольку Y – случайная переменная. Критерий проверки значимости R² имеет F-распределение. Это распределение обладает двумя степенями свободы: одно значение в числителе критерия проверки (обозначается v1), второе – в знаменателе (v2). В критерии проверки для R² числителю соответствует степень свободы 1 и знаменателю – n – 2 степеней свободы. Сам критерий проверки для R² рассчитывается так:

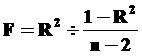
Для скорректированного R² критерий проверки вычисляется так:

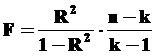
где n – число наблюдений, k – число независимых переменных в уравнении регрессии. Этот критерий проверки имеет F– распределение с со степенями свободы v1 = k – 1 и v2 = n – k.

Также для множественной регрессии имеет смысл рассчитать частные коэффициенты детерминации и . Но перед требуется обпределить парные коэффициенты корреляции между переменными модели: , , и т. д. Их рассчитывают для определения тесноты связи между переменными модели, на основе значения парных коэффициентов корреляции можно принять решение о включении или невключении факторной переменной в итоговую редакцию модели. Парные линейные коэффициенты корреляции определяются на основе формулы:

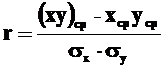
где σх и σу – среднеквадратические отклонения выборочных значений показателей х и у, для которых рассчитывается коэффициент корреляции, от выборочной средней. Величина среднеквадратического отклонения выборочного значения какого-либо показателя (например, х), как вы помните из курса статистики, равна квадратному корню из его дисперсии:

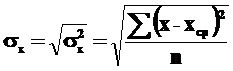
Коэффициент множественной корреляции для оценки зависимости результирующей переменной от факторных в парной регрессии рассчитывается по следующей формуле:

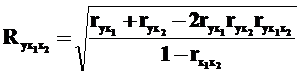
Этот коэффициент колеблется в пределах от 0 до 1 (колебания значений переменной Y абсолютно не зависят или полностью зависят от изменения значений факторов X), чем его значение ближе к 1, тем полнее учтены все факторы, влияющие на Y.

В общем случае формула коэффициента множественной корреляции выглядит так:

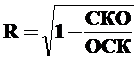
Частные коэффициенты детерминации в многофакторных моделях служат для анализа тесноты связи между результативной и одной из факторных переменных при неизменном значении остальных факторов. Они показывают, на сколько в процентном соотношении изменится значение зависимой переменной при изменении данного фактора и неизменных прочих:

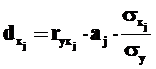
где – парный коэффициент корреляции факторной переменной j и зависимой переменной Y, aj – оценка соответствующего коэффициента регрессии при данном факторе в уравнении регрессии, и σу – среднеквадратические отклонения значений рассматриваемого фактора и Y.

Частные коэффициенты корреляции используются для измерения тесноты связи между данным фактором и зависимой переменной модели при неизменных прочих факторах:

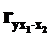·  – при одном неизменном факторе x2 – коэффициент частной корреляции первого порядка;

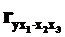·  – при двух неизменных факторах x2 и x3 – коэффициент частной корреляции второго порядка;

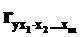·  – при неизменном действии всех факторов, включенных в уравнение регрессии – коэффициент частной корреляции (m – 1)-го порядка.

Коэффициенты парной корреляции называют коэффициентами нулевого порядка.

Частные коэффициенты корреляции можно рассчитать в соответствии со следующей формулой:

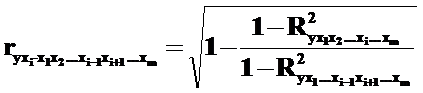
где 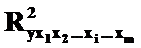– множественный коэффициент детерминации всего комплекса из m факторов с Y;

– показатель детерминации, но для модели, не включающей фактор xi.

Помимо этого, коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты более низких порядков по формуле:

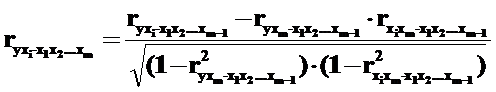
При двух факторах и i=1 данная формула примет вид:

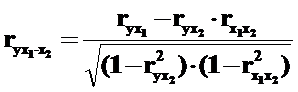
При двух факторах и i=2 данная формула будет выглядеть:

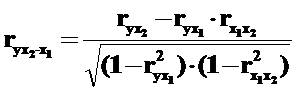
Помимо этих показателей, влияние отдельных факторов на результирующую переменную в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, определяемых по формуле

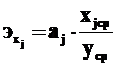
где xjср – среднее значение соответствующей факторной переменной, уср – средней значение результирующей переменной, aj – коэффициент при данном факторе в уравнении регрессии. Они показывают, на сколько процентов изменится величина результирующей переменной при изменении данного фактора на 1 % и неизменных прочих.

3.2.5. Тестирование выполнения допущений метода наименьших квадратов в модели линейной регрессии

Чтобы осуществить проверку модели на выполнение допущений метода наименьших квадратов, необходимо проверить модель на:

·  гетероскедастичность: является ли распределение остатков, ошибок регрессии постоянным (гомоскедастичным), или же нет;

·  автокорреляцию: являются ли значения остатков, ошибок независимыми, или имеет место явление автокорреляции остатков;

·  мультиколлинеарность: являются ли независимые переменные некоррелированными.

Существует большое число тестов для проверки на гетероскедастичность: тест ранговой корреляции Спирмена, тест Глейзера, тест, тест Голдфелда-Квандта, Бреуша-Пагана[31]… Одним из наиболее популярных тестов является тест Голдфелда-Квандта. Как правило, его применяют, если есть предположение о прямой зависимости дисперсии ошибки от величины некоторой независимой переменной модели. Для этого надо действовать по следующему алгоритму:

1)  все наблюдения упорядочиваются по величине независимой переменной, относительно которой есть подозрение на гетероскедастичность;

2)  остатки в этой упорядоченной совокупности делят на две равных группы, при чем находящиеся посредине между ними d наблюдений исключаются из рассмотрения (d обычно равно около ¼ от общего количества наблюдений);

3)  рассчитывается две независимых регрессии по первой и второй группе, количество наблюдений в которых составляет n/2–d/2 (при этом должно быть n/2 – d/2 > k + 1, где k – число независимых переменных), и находятся соответствующие остатки для первой и для второй регрессии е1 и е2;

4)  если предположение о прямой зависимости дисперсии ошибки от величины данной независимой переменной верно, то в первой группе сумма квадратов остатков (а значит и их дисперсия) будет меньше, чем во второй; затем рассчитывают критерий Голдфелда-Квандта: в случае предположения прямой пропорциональности между величиной дисперсии отклонений и значением независимой переменной сумму квадратов остатков во второй группе делят на сумму квадратов остатков в первой. Рассчитанный критерий имеет F-распределение с (n/2–d/2–k) и (n/2–d/2–k) степенями свободы. В случае обратной пропорциональности дисперсии отклонений значению независимой переменной сумму квадратов остатков в первой группе делят на сумму квадратов остатков во второй, распределение критерия также имеет вид F-распределения с теми же степенями свободы.

В случае наличия гетероскедастичности остатков для определения параметров регрессии применяется обобщенный метод наименьших квадратов (Generalized Least Squares, GLS). Он применяется к преобразованным данным и позволяет получать оценки, которые не только обладают свойством несмещенности, но имеют наименьшие выборочные дисперсии.

Автокорреляция (сериальная корреляция) – явление зависимости величины остатков друг от друга, поскольку текущие значения Y находятся под влиянием величины прошлых значений. Автокорреляция может появиться из-за недоучета (опущения) переменных, неверной формы функции, оценивающей зависимость результирующей переменной от факторных (например, линейная модель, в то время как она должна быть нелинейной) … Особенно подвержены автокорреляции данные временных рядов показателей.

Зависимость между остатками описывается также с помощью уравнения регрессии:

где остаток εi находится под влиянием величины остатка предыдущего наблюдения εi-1 и какого-либо текущего значения случайной переменной zi. Эта форма функции называется авторегрессионой функцией первого порядка (АР(1)), так как только один предшествующий период учтен при оценивании зависимости остатков.

В случае, когда предполагается зависимость текущего остатка от величин остатков двух и более предшествующих периодов, авторегрессионые функции имеют следующий вид:

Регрессионная модель позволяет получить несмещенную оценку с наименьшей дисперсией тогда, когда остатки независимы друг от друга. Когда существует автокорреляция остатков, то коэффициенты регрессии не смещены, но стандартные ошибки будут недооценены, и проверки коэффициентов регрессии будут ненадежны.

Для проверки на наличие автокорреляции остатков в модели можно построить график зависимости остатков от времени и определить автокорреляцию визуально, либо воспользоваться критерием Дарбина-Уотсона:

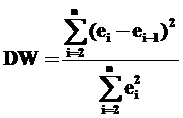
Согласно эмпирическому правилу, если критерий Дарбина-Уотсона равен 2, то не существует положительной автокорреляции, если он равен 0, то имеет место совершенная положительная автокорреляция, а если он равен 4, то имеет место совершенная отрицательная автокорреляция. Однако, данный критерий имеет выборочное распределение, базирующееся на специальной таблице[32]. Это выборочное распределение обладает двумя критическими значениями dL и dU.

В процессе проверки модели на автокорреляцию остатков с помощью этого критерия проверяется следующие гипотезы:

H0: нет автокорреляции, если dU ≤ DW ≤ 4 – dU;

H1: положительная автокорреляция при DW < dL;

отрицательная автокорреляция при DW > 4 – dL.

К сожалению, в составе данного распределения существуют зоны неопределенности, где результаты могут указывать как наличие, так и на отсутствие автокорреляции остатков:

dL < DW < dU или 4 – dU < DW < 4 – dL.

Для применения критерия Дарбина-Уотсона существуют некоторые ограничения.

Во-первых, он неприменим к моделям с лаговыми значениями зависимого признака, включаемыми в модель как фактор наряду прочими (авторегрессионые модели). Для тестирования на автокорреляцию в таких моделях используется h-критерий Дарбина.[33]

Во-вторых, при проверке на автокорреляцию более высоких, чем первый, порядков следует применять иные методы.[34]

В-третьих, критерий Дарбина-Уотсона дает достоверные результаты только в относительно больших выборках, не менее 15 – 20 наблюдений.

Для того, чтобы решить проблему автокорреляции, сначала следует рассмотреть возможность исключения переменных из модели или изменение формы функциональной зависимости результирующей переменной от переменных-факторов. Если это не приводит к успешному исключению автокорреляции остатков, можно применить процедуру Кокрана-Оркатта[35].

Если некоторые или все независимые переменные в модели множественной регрессии являются высококоррелированными, трудно в рамках регрессионной модели разграничить их отдельные влияния на Y. Это также может означать наличие между высококоррелированными независимыми переменными мультиколлинеарности – линейной зависимости, то есть воздействия одного фактора на другой. Высококоррелированные переменные действуют в одном направлении, в результате чего модель не может изолировать влияние каждой из переменных-факторов на результат. При мультиколлинеарности коэффициенты регрессии нестабильны по их статистической значимости, величине и знаку, а стало быть – ненадежны. Значения R2 могут быть высоки, но стандартные ошибки также высоки, отсюда t-критерии малы, отражая недостаток значимости.

Коэффициенты интеркорреляции (то есть парной корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, то есть находятся между собой в линейной зависимости, если парный коэффициент корреляции между ними равен или превышает 0,8[36].

Поскольку одним из условий построения уравнения множественной регрессии является независимость факторов, коллинеарность факторов нарушает это условие. Если факторы явно коллинеарны, то один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименее тесную связь с другими факторами.

В отношении мультиколлинеарности могут быть предприняты некоторые меры:

1)  Исключение из модели тех факторов, которые являются высококоррелированными с остальными. Однако, возможно, что данные переменные были включены в модель в соответствии с результатами тщательного предварительного качественного теоретико-экономического анализа, а значит будет не совсем оправдано исключать их только для того, чтобы улучшить статистические результаты;

2)  Увеличение объема выборки по принципу: чем больше данных, тем меньше дисперсии оценок МНК. Проблема в реализации этого варианта – необходимо найти дополнительные данные;

3)  Преобразование факторов таким образом, чтобы уменьшить корреляцию между ними, например, переход от исходных переменных к их линейным комбинациям, не коррелированным друг с другом (метод главных компонент[37]).

3.2.6. Прогнозирование на основе эконометрических моделей (на примере модели из одного уравнения)

В прогнозных расчетах по уравнению регрессии определяется предсказываемое значение Yi+l как точечный прогноз величины Y при заданных 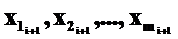путем подстановки данных значений независимых переменных в уравнение регрессии. Однако точечный прогноз не учитывает еще одного элемента, входящего в регрессионную модель – стохастической компоненты, точнее – погрешности прогноза вследствие ее существования. Поэтому точечный прогноз обычно дополняется расчетом ошибки для значения зависимой переменной Y, рассчитанного по уравнению регрессии.

Для определения интервала, в котором находятся возможные значения зависимой переменной уравнения регрессии при известных значениях независимых переменных, необходимо учитывать ошибки двух разновидностей.

Во-первых, ошибки могут быть вызваны рассеиванием фактических значений Y в соответствии с произведенными наблюдениями относительно линии регрессии. Их можно учесть, рассчитав по следующей формуле:

.

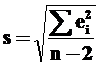Подкоренное выражением представляет собой как раз меру разброса фактических значений зависимой переменной вокруг линии регрессии – остаточную дисперсию. Извлекая из нее корень, находим стандартную ошибку Y.

Во-вторых, заданные для модели коэффициенты регрессии являются нормально распределенными случайными величинами. Обусловленные этим отклонения учитываются с помощью умножения значения s на поправочное выражение. Для модели парной линейной регрессии средняя величина отклонения прогнозируемого значения от линии регрессии, таким образом, насчитывается по формуле:

,

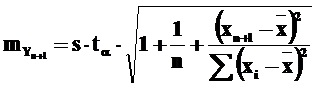где n – число наблюдений, l – шаг прогноза, tα – табличное значение t-статистики при уровне значимости α (количество степеней свободы – n–2), xi – наблюдаемое значение независимой переменной в наблюдении i, – среднее значение x, xn+l – прогнозное (заданное) значение независимой переменной на шаге прогноза l.

Отсюда верхняя и нижняя границы интервала предсказания определятся как

.

В общем случае модели множественной линейной регрессии среднюю величину возможного отклонения реального значения показателя от рассчитанного с помощью имеющегося уравнения регрессии можно найти следующим образом.

Пусть модель множественной регрессии, как и описывалось ранее, имеет вид:

где Y вектор-столбец значений зависимой переменной (Y1, Y2, …, Ym); α – вектор-столбец коэффициентов (α0, α1, α2, …, αn); ε вектор-столбец стохастических компонент (ошибок) (ε0, ε1, ε2, …, εm); Х – матрица независимых переменных размерности mxn, причем первый ее столбец состоит из единиц.

Предположим теперь, что есть еще один набор (вектор-строка) xn+1 (первый элемент, соответствующий свободному члену уравнения, равен 1) независимых переменных и известно, что соответствующая ему зависимая переменная удовлетворяет данной модели, те есть

где также должны соблюдаться все предпосылки МНК. Требуется по Y, X, xn+1 оценить Yn+1.

Точечный прогноз величины Yn+1 находим так же, как и в случае с парной регрессией: подставляем в уравнение регрессии соответствующие значения xn+1. Остается оценить ошибку прогноза. Ее найдем в соответствии со следующей формулой, которая является по отношению к приведенной выше формуле средней величины отклонения прогнозируемого значения от линии регрессии для уравнения парной регрессии общей:

.

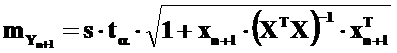3.3. Разработка индикаторов

Индикатор – показатель, обычно интегральный, количественно определяющий качественные характеристики процесса.

Индикаторы определяются как параметры границ, в пределах которых система, включающая организационные механизмы, технологические связи, материальные и финансовые потоки, может устойчиво функционировать и развиваться. В отличие от «показателя», дающего лишь количественную констатацию, индикатор носит векторный, направленный характер. Индикаторы имеют предельные пороговые (минимальные и максимальные) значения: уровни прибыльности, налоговых ставок, режимов развития многоресурсных систем...

Особое место занимает определение и использование пороговых значений индикаторов, призванных сигнализировать о приближении критического состояния объекта управления и необходимости изменения стратегии развития объекта, т. е. включение регуляторов:

·  индикаторы «тревоги»;

·  индикатор «экстремального положения»;

·  индикатор «банкротство» и т. д.

Внутри предельных границ образуется так называемый «коридор» – необходимый и достаточный для принятия управленческого решения, но при этом необходимо установление адекватных пороговых значений «коридора». Реальность действия индикатора определяется не только количественными характеристиками. Важно, чтобы индикатор был инструментальным, для которого существуют регуляторы прямого воздействия на объект управления.

Формирование индикаторов – процесс, увязанный во временном аспекте. В данном случае ставится целью получение единого индикатора, характеризующего состояние объекта управления. Актуален вопрос о величине удельного веса каждого из отдельных регуляторов при их агрегировании. Если какие – либо регуляторы линейно или нелинейно зависят друг от друга, то в системе присутствует ненужная информация, искажающая результаты анализа, прогнозирования и, как следствие, результаты планирования. Для этих целей необходим множественный анализ всей совокупности заданных показателей.

Индикаторы социально-экономического развития являются центральным элементом системы индикативного планирования, в рамках которой они играют роль планово-прогнозного показателя: планового – в смысле обозначенного целевого ориентира социально-экономического развития, прогнозного – имея в виду вероятностный характер достижения этой цели. Индикаторы характеризуют желаемую ситуацию, состояние, а не плановый норматив. Основной смысл их использования – оценка тенденций развития с точки зрения результата.

В нашей стране вопрос об индикаторах социально-экономического развития стал активно обсуждаться в связи с идеей разработки системы индикаторов экономической безопасности. Деятельность по их выработке и утверждению велась в рамках Совета Безопасности Российской Федерации с середины 1990-х гг., в том числе с привлечением других учреждений и органов (тех же органов государственной статистики). Результатом ее, в частности, стало утверждение в феврале 2000 г. следующих пороговых значений ряда таких индикаторов:

Таблица 4. Индикаторы экономической безопасности в Российской Федерации

В мировой практике накоплен большой опыт по разработке статистических индикаторов, отражающих различные аспекты благосостояния населения. Основные социально-экономические индикаторы, используемые в настоящее время федеральным статистическим ведомством России включают в себя схожие по смыслу показатели.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26