Найдите: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал (9,15; 10,4) . Постройте графики функций распределения и плотности распределения.
Вариант 2
А). Сколько перестановок можно получить из букв слова БОЧКА ?Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 245752235?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПРОСЬБА составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?
Решить уравнение 
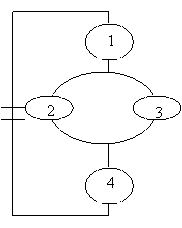
На рисунке приведена схема электрической цепи. События: |
={элемент k работает}; С={ в цепи нет разрыва}. Выразить события 
и 
через события
.а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;
xi | -1 | 2 | 3 | 4 |
pi | 0,4 | 0,2 | 0,1 | * |
Найти закон распределения случайных величин а )Z=X+2Y; б)U=XY.
xi | -2 | -1 | 1 | 2 |
pi | 0,2 | 0,1 | 0,3 | 0,4 |
yi | -2 | 0 | 1 | 4 |
pi | 0,1 | 0,2 | 0,1 | 0,6 |
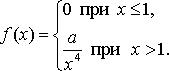
Найдите: 1) функцию распределения F(x)и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал (0: 5) . Постройте графики функций распределения и плотности распределения
Вариант 3
А). Сколько перестановок можно получить из букв слова АЛЬБОМ?Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 345642353 ?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПРОСТЫНЯ составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв? Решить уравнение
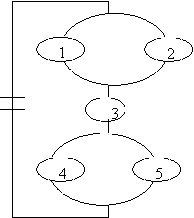
На рисунке приведены схемы электрических цепей. События: |
|
7. Точка (c, q) наудачу выбирается из квадрата с вершинами (0,0), (1,0), (1,1), (0,1). Найдите вероятность того, что корни уравнения х2 +сх + q = 0 окажутся действительными и одного знака.
В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих шаров наудачу взят один шар. а)Найдите вероятность того, что взят белый шар. б) Выбранный шар оказался белым. Какова вероятность, что он взят из первой урны? Наблюдениями установлено, что в некоторой местности в июле в среднем бывает 12 дождливых дней. Какова вероятность того, что из восьми случайно выбранных в этом месяце дней а ) ровно три окажутся дождливыми; б) дождливыми окажутся хотя бы два дня; в) дождливыми будут не более 7 дней? Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени t равна 0,002. Найдите вероятность того, что за время t откажут ровно 3 элемента. Вероятность того, что станок-автомат произведет годную деталь, равна 9/11. за смену было изготовлено 330 деталей. Определить вероятность того, что среди них а) 40 бракованных; б) бракованных деталей не более 40, но не менее 2. Дан ряд распределения случайной величины Х.а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;
xi | 1 | 2 | 5 | 7 |
pi | 0,3 | 0,2 | 0,1 | * |
Найти закон распределения случайных величин а )Z=3X+Y; б)U=XY.
xi | 0 | 1 | 2 | 4 |
pi | 0,1 | 0,1 | 0,3 | 0,5 |
yi | -2 | 0 | 2 | 4 |
pi | 0,1 | 0,2 | 0,1 | 0,6 |
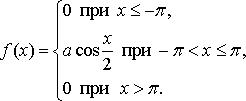
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
