Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал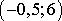 
. Постройте графики функций распределения и плотности распределения.
Вариант 19
А). Сколько перестановок можно получить из букв слова ПРОБКА?Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
А). Сколько перестановок можно получить из цифр числа 4756473847?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
Из букв слова ПРАВИЛО составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?
Решить уравнение
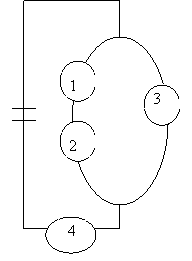
На рисунке приведена схема электрической цепи. События: |
|
={элемент k работает}; С={ в цепи нет разрыва}. Выразить события 
и 
через события 
.
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;
xi | 2 | 4 | 6 | 7 |
pi | 0,4 | 0,3 | 0,1 | * |
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
xi | -2 | 0 | 1 | 2 |
pi | 0,2 | 0,1 | 0,2 | 0,5 |
yi | -1 | 0 | 2 | 4 |
pi | 0,2 | 0,2 | 0,5 | 0,1 |
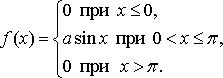
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения.
Вариант 20
А). Сколько перестановок можно получить из букв слова ПРИЮТ?Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
А). Сколько перестановок можно получить из цифр числа 2847563473?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
Из букв слова ПОХЛЕБКА составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?
Решить уравнение
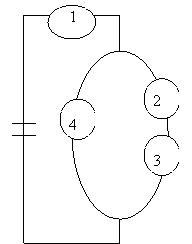
. 5. | На рисунке приведена схема электрической цепи. События: |
|
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;
xi | 0 | 1 | 3 | 5 |
pi | 0,1 | 0,3 | 0,1 | * |
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
xi | 0 | 1 | 2 | 4 |
pi | 0,1 | 0,1 | 0,3 | 0,5 |
yi | -2 | 0 | 2 | 4 |
pi | 0,1 | 0,2 | 0,1 | 0,6 |
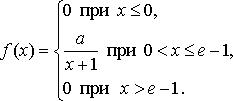
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения.
Вариант 21
А). Сколько перестановок можно получить из букв слова ОРХИДЕЯ?Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
А). Сколько перестановок можно получить из цифр числа 4756349845?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
Из букв слова ПОЧИНКА составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?
Решить уравнение 
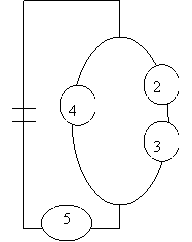
5. | На рисунке приведена схема электрической цепи. События: |
|
Курс жука перпендикулярен курсу улитки. В специализированную больницу поступают в среднем 50% больных с заболеванием А, 30% — с заболеванием В, 20% — с заболеванием С. Вероятность полного излечения болезни А равна 0,7; для болезней В и С эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найдите вероятность того, что этот больной страдал заболеванием А. Транзисторный радиоприемник смонтирован на 6 полупроводниках, для которых вероятность брака равна 0,1. приемник отказывает при наличии не менее двух бракованных полупроводников. Найти вероятность того, что: а) откажут ровно 5 полупроводников; б) приемник будет работать; в) приемник откажет. Пусть вероятность того, что пассажир опоздает к отправлению поезда, равна 0,02. Найдите число наиболее вероятное число опоздавших из 855 пассажиров. Какова вероятность того, что опоздает меньше 5 пассажиров? В цехе имеется 90 станков, работающих независимо друг от друга. Для каждого станка вероятность быть включенным равна 0,9. Вычислите вероятность того, что в некоторый момент времени включенными окажутся а) ровно 50 станков; б) от 60 до 75 станков. Дан ряд распределения случайной величины Х.
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;
xi | -2 | 1 | 3 | 4 |
pi | 0,4 | 0,2 | 0,1 | * |
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
xi | -4 | 0 | 1 | 2 |
pi | 0,2 | 0,1 | 0,2 | 0,5 |
yi | -1 | 0 | 2 | 4 |
pi | 0,2 | 0,2 | 0,5 | 0,1 |
|
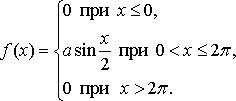
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
