Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения.

Вариант 16

А). Сколько перестановок можно получить из букв слова ВОТЧИНА ?
Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?

А). Сколько перестановок можно получить из цифр числа1928339212 ?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?

Из букв слова ПРИБОР составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?

Решить уравнение

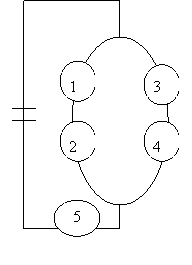
5.   

На рисунке приведена схема электрической цепи. События: ={элемент k работает}; С={ в цепи нет разрыва}. Выразить события и через события и .

Из 10 студентов 7 имеют спортивные разряды. Найти вероятность того, что среди выбранных наудачу 5 студентов спортивный разряд имеют а)3 человека; б) менее трех человек. На окружности радиуса R наудачу поставлены три точки А, В и С. Какова вероятность того, что треугольник АВС не является остроугольным? Из 20 студентов, пришедших на экзамен, 8 подготовлены отлично, 6 — хорошо, 4 — посредственно и 2 — плохо. В экзаменационных билетах имеется 40 вопросов. Студент, подготовленный отлично, знает все вопросы, хорошо — 35, посредственно —25 и плохо — 10 вопросов. Некоторый студент ответил на все 3 вопроса билета. Найдите вероятность того, что он подготовлен: а) хорошо; б) плохо. Баскетболист делает 8 бросков мячом в корзину. Вероятность попадания мяча при каждом броске одинакова и равна 0,4. найти вероятность того, что а) баскетболист ровно 4 раза попадет мячом в корзину; б) попаданий в корзину будет менее четырех; в) попаданий мячом будет не более 5. При изготовлении радиоламп в среднем бывает 2% брака. Найдите вероятность того, что в партии из 200 ламп не более двух бракованных. Вероятность того, что станок-автомат произведет годную деталь, равна 8/9. за смену было изготовлено 300 деталей. Определить вероятность того, что среди них а) 40 бракованных; б) бракованных деталей не более 40, но не менее 20. Дан ряд распределения случайной величины Х.
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;

xi

2

4

6

7

pi

0,2

0,3

*

0,1
Даны законы распределения двух случайных величин Х и Y:
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.

xi

-1

0

2

4

pi

0,2

0,1

0,2

0,5

yi

-2

-1

1

2

pi

0,1

0,1

0,2

0,6
Случайная величина Х задана функцией плотности распределения

Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения.

Вариант 17

А). Сколько перестановок можно получить из букв слова ВОЗРАСТ ?
Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?

А). Сколько перестановок можно получить из цифр числа174757182 ?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?

Из букв слова ПРИБОЙ составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?

Решить уравнение

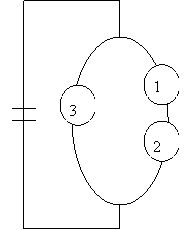
5.   

На рисунке приведена схема электрической цепи. События: ={элемент k работает}; С={ в цепи нет разрыва}. Выразить события и через события и .

В лотерее «Спортлото 6 из 45» участник лотереи, правильно угадавший 4, 5 или 6 видов спорта из 30 , получает денежный приз. Найти вероятность того, что данный участник угадает а) 5 видов спорта; б) получит денежный приз. Плоскость разграфлена параллельными прямыми, находящимися на расстоянии 2а друг от друга. На плоскость наудачу брошена монета радиуса г<a. найти вероятность того, что монета не пересечет ни одной из прямых. Из 18 стрелков 5 попадают в мишень с вероятностью 0,8;— с вероятностью 0,7; 4 — с вероятностью 0,6 и 2 — с вероят­ностью 0,5. Наудачу выбранный стрелок не попал в мишень. К какой группе вероятнее всего принадлежит этот стрелок? Среди коконов некоторой партии 20% цветных. Какова вероятность того, что среди 10 отобранных коконов а) цветных будет 4 кокона; б) цветных коконов будет не менее шести; в) цветных коконов будет не более 8. Аппаратура содержит 2000 одинаковых надежных элементов, вероятность отказа для каждого из которых равна 0,0005. Какова вероятность отказа аппаратуры, если он наступает при отказе хотя бы одного из элементов? Вероятность того, что деталь не прошла проверку ОТК равна р = 0,3. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных а) ровно 60; б) от 70 до 100. Дан ряд распределения случайной величины Х.
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;

xi

0

3

6

7

pi

0,1

*

0,1

0,3
Даны законы распределения двух случайных величин Х и Y:
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.

xi

-2

-1

0

1

pi

0,2

0,1

0,3

0,4

yi

-2

-1

1

4

pi

0,1

0,1

0,5

0,3
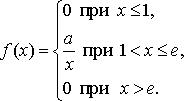
Случайная величина Х задана функцией плотности распределения

Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения.

Вариант 18

А). Сколько перестановок можно получить из букв слова ВОЛЫНКА?
Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?

А). Сколько перестановок можно получить из цифр числа 3857462642?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?

Из букв слова ПРОЧЕРК составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?

Решить уравнение

5.   

На рисунке приведена схема электрической цепи. События: ={элемент k работает}; С={ в цепи нет разрыва}. Выразить события и через события и .

В аудитории находятся 20 студентов. 12 из них изучают английский язык, а остальные 8 – французский. Случайным образом для уборки территории отбираются 5 студентов. Найти вероятность того, что среди них а) ровно 3 изучают английский язык; б) студентов изучающих французский больше. На отрезок АВ длиной 12 см наугад ставят точку М. Найдите вероятность того, что площадь квадрата, построенного на отрезке АМ, будет заключена между 36 см2 и 81 см2. Для сдачи экзамена студентам было необходимо подгото­вить 30 вопросов. Из 25 студентов 10 подготовили все вопросы,8 студентов подготовили по— 25 вопросов, 5 —по 20 вопросов и 2 — по15 вопросов. Вызванный студент ответил на поставленный вопрос. Найдите вероятность того, что этот студент: а) подготовил все вопросы; б) подготовил только половину вопросов. По каналу связи передается 8 сообщений. Каждое из них независимо от других с вероятностью 0,1 искажается помехами. Найти вероятности следующих событий: а) из 8 событий ровно 5 искажаются помехами; б) искажаются помехами не более половины всех передаваемых сообщений; в) помехами искажается более 6 сообщений. По данным ОТК в среднем 3% изделий требуют дополнительной регулировки. Вычислите вероятность того, что из 200 изделий 4 потребуют дополнительной регулировки. Вероятность выхода конденсатора из строя в течение времени t равна 0,3. Вычислите вероятность того, что за этот промежуток времени из имеющихся 150 конденсаторов выйдет из строя а) ровно 60 конденсаторов; б) от 40 до 80 конденсаторов. Дан ряд распределения случайной величины Х.
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;

xi

-2

1

3

4

pi

0,4

0,2

0,1

*
Даны законы распределения двух случайных величин Х и Y:
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.

xi

-1

0

1

2

pi

0,1

0,1

0,3

0,5

yi

-4

0

2

4

pi

0,1

0,4

0,1

0,2
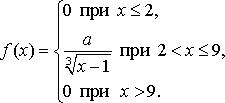
Случайная величина Х задана функцией плотности распределения  

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18