Для описания многих практически важных свойств случайной величины необходимо знание не только ее математического ожидания, но и отклонения возможных ее значений от среднего значения.
Дисперсия случайной величины — мера разброса случайной величины, равная математическому ожиданию квадрата отклонения случайной величины от ее математического ожидания.
![]() .
.
Принимая во внимание свойства математического ожидания, легко показать что
![]()
Казалось бы естественным рассматривать не квадрат отклонения случайной величины от ее математического ожидания, а просто отклонение. Однако математическое ожидание этого отклонения равно нулю. Это объясняется тем, что одни возможные отклонения положительны, другие отрицательны, и в результате их взаимного погашения получается ноль. Можно было бы принять за меру рассеяния математическое ожидание модуля отклонения случайной величины от ее математического ожидания, но как правило, действия связанные с абсолютными величинами, приводят к громоздким вычислениям.
Свойства дисперсии:
1. Дисперсия постоянной равна нулю.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
3. Если x и y независимые случайные величины, то дисперсия суммы этих величин равна сумме их дисперсий.
Средним квадратическим отклонением случайной величины (иногда применяется термин «стандартное отклонение случайной величины») называется число равное ![]() .
.
Среднее квадратическое отклонение, является, как и дисперсия, мерой рассеяния распределения, но измеряется, в отличие от дисперсии, в тех же единицах, которые используют для измерения значений случайной величины.
Решение задач:
1) Дана случайная величина Х:
xi | -3 | -2 | 0 | 1 | 2 |
pi | 0,1 | 0,2 | 0,05 | 0,3 | 0,35 |
Найти М(х), D(X).
Решение:
![]() .
.
![]() =9
=9![]() =2,31.
=2,31.
![]() .
.
2) Известно, что М(Х)=5, М(Y)=2. Найти математическое ожидание случайной величины Z=6X-2Y+9-XY.
Решение: М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.
Пример: Известно, что D(Х)=5, D(Y)=2. Найти математическое ожидание случайной величины Z=6X-2Y+9.
Решение: D(Z)=62 D(Х)-22 D(Y)+0=180-8=172.
Тема 7.
Непрерывные случайные величины
Задача 14
Случайная величина, значения которой заполняют некоторый промежуток, называется непрерывной.
Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).
![]()
Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.
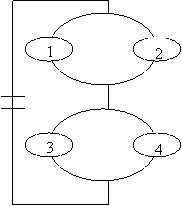
Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.
Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.
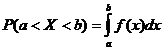
Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:
![]()
Свойства плотности распределения.
1) Плотность распределения – неотрицательная функция.
![]()
2) Несобственный интеграл от плотности распределения в пределах от - ¥ до ¥ равен единице.
![]()
Решение задач.
1. Случайная величина подчинена закону распределения с плотностью:
![]()
Требуется найти коэффициент а, определить вероятность того, что случайная величина попадет в интервал от 0 до ![]() .
.
Решение:
Для нахождения коэффициента а воспользуемся свойством 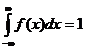 .
.
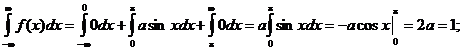
![]()
![]()
2 .Задана непрерывная случайная величина х своей функцией распределения f(x).
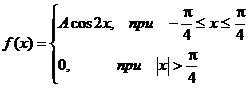
Требуется определить коэффициент А, найти функцию распределения, определить вероятность того, что случайная величина х попадет в интервал ![]() .
.
Решение:
Найдем коэффициент А.
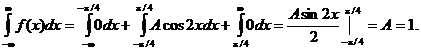
Найдем функцию распределения:
1) На участке ![]() :
: ![]()
2) На участке ![]()
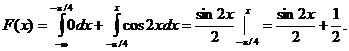
3) На участке ![]()
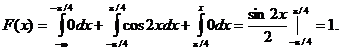
Итого: 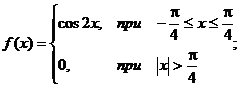

Найдем вероятность попадания случайной величины в интервал ![]() .
.

Ту же самую вероятность можно искать и другим способом:
![]()
Вариант 1
А). Сколько перестановок можно получить из букв слова ВАЛЕТ ?Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 125367266?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПРОГУЛКА составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?
Решить уравнение
5. | На рисунке приведена схема электрической цепи. События: |
|
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;
xi | 2 | 4 | 6 | 7 |
pi | 0,4 | 0,3 | 0,1 | * |
Найти закон распределения случайных величин а )Z=2X+Y; б)U=XY.
xi | -1 | 0 | 1 | 2 |
pi | 0,2 | 0,1 | 0,3 | 0,4 |
yi | -2 | 0 | 1 | 2 |
pi | 0,1 | 0,2 | 0,1 | 0,6 |
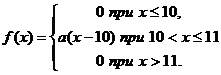

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |