Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения.
Вариант 22
1. А). Сколько перестановок можно получить из букв слова ОРГАНИЗМ?
Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
2. А). Сколько перестановок можно получить из цифр числа 2948576488?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
3. Из букв слова ПОДХАЛИМ составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?
4. Решить уравнение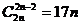 
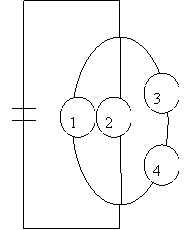
5. | На рисунке приведена схема электрической цепи. События: |
|
={элемент k работает}; С={ в цепи нет разрыва}. Выразить события 
и 
через события 
.
6. Мама испекла десять пирожков с начинкой. Внешне пирожки были одинаковые. Среди десяти пирожков четыре были с мясом, а остальные с капустой. Определить вероятность того, что среди взятых наудачу пяти пирожков окажется а)три мясных; б) не более трех капустных.
7. Королева Елизавета велела белошвейке вышить на ленте длины а две розы. Найти вероятность того, что расстояние между розами окажется меньше а/4.
8. В первой урне находится один белый и 9 черных шаров, а во второй — один черный и 5 белых шаров. Из каждой урны удалили случайным образом по одному шару, а оставшиеся шары ссыпали в третью (свободную) урну. Найдите вероятность того, что шар, вынутый из третьей урны, окажется белым.
9. Радиоэлектронный комплекс самолета-бомбардировщика включает в себя 8 объектов. Вероятность работы каждого объекта равна 0,9. Объекты выходят из строя независимо один от другого. Найти вероятность того, что : а) откажет хотя бы один объект; б) откажут ровно шесть объектов; в) откажут не менее шести объектов.
10. Найдите вероятность того, что среди 200 изделий окажется не более трех бракованных, если в среднем бракованные изделия составляют 1%.
11. Вероятность изготовления детали со стандартными размерами равна 0,8. Вычислите вероятность того, что среди 300 деталей стандартными будут от 200 до 250.
12. Дан ряд распределения случайной величины Х.
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;
xi | -1 | 2 | 3 | 4 |
pi | 0,4 | * | 0,15 | 0,15 |
13. Даны законы распределения двух случайных величин Х и Y:
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
xi | -1 | 0 | 1 | 2 |
pi | 0,4 | 0,1 | 0,3 | 0,2 |
yi | -2 | 0 | 1 | 2 |
pi | 0,1 | 0,3 | 0,1 | 0,5 |
14.Случайная величина Х задана функцией плотности распределения
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения.
Вариант 23
А). Сколько перестановок можно получить из букв слова НАТУРЩИК?Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
А). Сколько перестановок можно получить из цифр числа 48375637558 ?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
Из букв слова ПЛОТИНА составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?
Решить уравнение
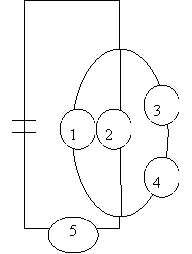
5. | На рисунке приведена схема электрической цепи. События: |
|
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал
[3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;
xi | 2 | 4 | 6 | 7 |
pi | * | 0,3 | 0,2 | 0,1 |
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
xi | -3 | -1 | 1 | 2 |
pi | 0,2 | 0,4 | 0,3 | 0,1 |
yi | -2 | -1 | 1 | 3 |
pi | 0,1 | 0,2 | 0,1 | 0,6 |
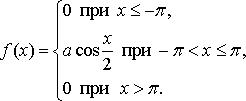
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
