некоторой полной группы событий H1, H2, …Hn.

События этой группы обычно называют гипотезами. Тогда

P(A) = P(H1)PH1(A) + P(H2) PH2(А) +…+ P(Hn)PHn(A) (1)

(формула полной вероятности), причем

P(H1) +P(H2) +…+ P(Hn) = 1.

Пусть в результате испытания произошло событие А, которое могло наступить только

вместе с одним из событий H1, H2,…Hn, образующих полную группу событий (они

называются гипотезами). Требуется найти вероятность событий H1, H2,… Hn после

испытания, когда событие А имело место, т. е. PA(Hi), i = 1,2,…n. Для нахождения этих вероятностей используют формулы Байеса (формулы гипотез):

PA (Hi) = (2)

Замечания.

1) Вероятности PA(H1) называются послеопытными (апостериорными) вероятностями

гипотез Hi, а вероятности P(Hi) - доопытными (априорными) вероятностями гипотез

Hi. Эти вероятности различаются.

2) Знаменатель в правой части формулы (2) совпадает с правой частью формулы (1) и

равен P(A).

Решение задач.

1.На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго.

а) Каков процент брака на конвейере?

б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?

Решение. Возьмем с конвейера наудачу одну деталь и рассмотрим событие А – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь: Нi – взятая наудачу деталь обработана на i-ом станке, i=1,2,3 .

Условные вероятности (в условии задачи они даны в форме процентов):

, , .

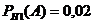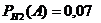Зависимости между производительностями станков означают следующее: 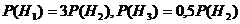. Причем P(H1) +P(H2) +P(H3) = 1,так как гипотезы образуют полную группу.

Для того, чтобы найти вероятности появления гипотез, нам придется решить систему вышеперечисленных уравнений. Решив ее, получим .

а) Полная вероятность того, что взятая наудачу с конвейера деталь – бракованная:

P(A) = P(H1)PH1(A) + P(H2) PH2(А) + P(H3)PH3(A)==.

Другими словами, в массе деталей, сходящих с конвейера, брак составляет 4%.

б) Пусть известно, что взятая наудачу деталь – бракованная. Пользуясь формулой Байеса, найдем условные вероятности гипотез:

,

,

.

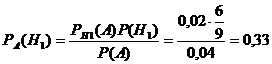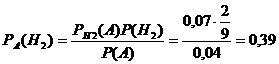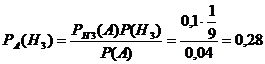Таким образом, доли деталей каждого станка среди бракованных деталей на конвейере для первого станка составляет 33%, второго – 39%, третьего – 28%.

Тема 5

Повторные испытания.

Задачи 9-11.

Формула Бернулли: Если производится n независимых испытаний, в каждом из которых событие А появится с вероятностью р, то вероятность того, что событие А появится ровно k раз в n испытаниях, выражается формулой, которую называют формулой Бернулли

Pn(k) = Cnkpk qn – k ,где q=1-p (1),

Иногда бывают полезны следующие формулы: Вероятность того, что событие A:

1) наступит n раз: ; (2)

2) не наступит ни разу: ; (3)

3) наступит хотя бы один раз: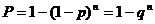 ; (4)

4) наступит не более k раз: 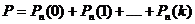(5)

или . (6)

5) наступит не менее k раз: 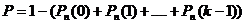(7)

или . (8)

Из формул (5)и(6), а также (7)и (8) выбирают ту, которая содержит меньше слагаемых.

Наивероятнейшее число наступлений события

Наивероятнейшее число m0 определяется из двойного неравенства

np - q m0 np + p (9)

Формула Пуассона (лучше использовать при .)

Теорема :Если вероятность p наступления события А в каждом испытании постоянна и близка к нулю (р), а число независимых испытаний n достаточно велико (), причем произведение np стремится к постоянному числу 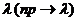то вероятность Pn(k) того, что в n независимых испытаниях событие А наступит k раз, приближенно равна: (11)

Локальная теорема Муавра-Лапласа (рекомендуется применять при npq).

Пусть в серии из n независимых испытаний вероятность наступления события А в каждом испытании равна р (0<p<1), q=1-p, . Если и величина является ограниченной, тогда 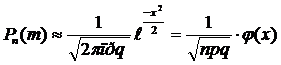(12).

Таблица значений функции приведена в приложении. Функция является четной, т. е =, монотонно убывающей при х>4 практически .

Интегральная теорема Муавра-Лапласа (удобно применять при npq).

Если n – велико, а р – отлично от 0 и 1, то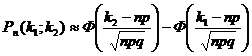

где 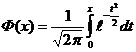- функция Лапласа. Таблица значений функции приведена в приложении. Функция является нечетной, т. е =-.Если х>4, то в силу монотонного возрастания функции .

Решение задач:

Полагая, что вероятность поражения мишени при одном выстреле равна 0,6, найти вероятности следующих событий:

1)  а) при 12 выстрелах мишень будет поражена 7 раз;

б) при 12 выстрелах мишень будет поражена менее 4 раз;

в) при 12 выстрелах мишень будет поражена не более 8 раз;

2)  Наивероятнейшее число выстрелов, которые поразят мишень при 125 сделанных выстрелах. И вероятность этого числа попаданий.

3)  При 200 выстрелах мишень будет поражена не менее 110, но не более 130 раз.

4) При 200 выстрелах мишень будет поражена не более 110 раз;

5) При 200 выстрелах мишень будет поражена не менее 115 раз.

6) На стрельбы пришла Полина Александровна. Для нее вероятность попадания в мишень равна 0,04. Найти вероятность того, что из 200 выстрелов Полина Александровна попадет в мишень 10 раз.

Решение:

1)  воспользуемся формулами Бернулли:

а) Р12(7)=;

б) при 12 выстрелах мишень будет поражена менее 4 раз означает, что мишень будет поражена 0, 1, 2 или 3 раза. Ищем Р12(0)+Р12(1)+Р12(2)+Р12(3)= +++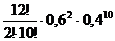0,000017+0,000302+0,002491+0,012457=0,12738.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18