Вариант 24
А). Сколько перестановок можно получить из букв слова МИНАРЕТ?Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
А). Сколько перестановок можно получить из цифр числа 4736275464?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
Из букв слова ПЛОМБИР составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?
Решить уравнение
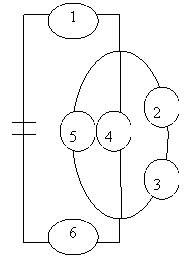
5. | На рисунке приведена схема электрической цепи. События: |
|
={элемент k работает}; С={ в цепи нет разрыва}. Выразить события 
и 
через события 
.
Внутренний круг и два кольца, ограниченные радиусами 2r и3r, а также 4r и 5r - закрашены. Определить вероятность попадания дротика в заштрихованную область. Имеется 10 монет, причем у одной из них герб с обеих сторон, а остальные монеты обычные. Наугад выбранную монету, не разглядывая, бросают 10 раз, причем при всех бросаниях она падает гербом кверху. Найдите вероятность того, что была выбрана монета с 2 гербами. Рабочий обслуживает 12 однотипных станков. Вероятность, что станок потребует внимания рабочего в течение промежутка времени Т, равна 1/3. Найти вероятность того, что за время Т а) 2 станка потребуют внимания рабочего; б) менее 2-х станков потребуют внимания рабочего; в) хотя бы 2 станка потребуют внимания рабочего. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на 1 веретене в течение 1 мин равна 0,003. Вычислите вероятность того, что в течение 1 мин произойдет не более двух обрывов Из большой партии продукции, содержащей 80% изделий первого сорта, наугад отбирают 200 изделий. Вычислите вероятность того, что среди отобранных будет а) ровно 80 изделий 1 сорта; б) не менее 50 и не более 90 изделий первого сорта. Дан ряд распределения случайной величины Х.
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал
[3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;
xi | 1 | 3 | 5 | 6 |
pi | * | 0,25 | 0,1 | 0,3 |
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
xi | -3 | 0 | 1 | 2 |
pi | 0,1 | 0,1 | 0,3 | 0,5 |
yi | -1 | 1 | 2 | 4 |
pi | 0,1 | 0,2 | 0,1 | 0,6 |
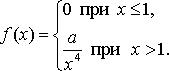
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения.
Вариант 25
А). Сколько перестановок можно получить из букв слова МОНЕТА?Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
А). Сколько перестановок можно получить из цифр числа 34765726374?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
Из букв слова ПЛОТНИК составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?
Решить уравнение
5. | На рисунке приведена схема электрической цепи. События: |
|
Внутренний круг и два кольца, ограниченные радиусами 2r и3r, а также 4r и 5r - закрашены. Определить вероятность попадания дротика в незаштрихованную область. При переливании крови надо учитывать группу крови донора и больного. Человеку, имеющему четвертую группу крови, можно перелить кровь любой группы; человеку со второй или третьей группой крови можно перелить кровь либо той же группы, либо первой; человеку с первой группой крови можно перелить только кровь первой группы Китайский завод изготавливает изделия, каждое из которых с вероятностью 1/3 оказывается дефектным. Для контроля продукции выбирается 8 изделий. Найти вероятность того, что а) ни в одном изделии не будет дефекта; б) не менее чем в трех изделий будет обнаружен дефект; в) ровно в пяти изделиях будет дефект. В зрительном зале находится 500 человек. Какова вероятность того, что среди них имеется 3 левши, если левши в среднем составляют 1%? Вероятность выхода конденсатора из строя в течение времени t равна 0,3. Вычислите вероятность того, что за этот промежуток времени из имеющихся 150 конденсаторов выйдет из строя а) ровно 50 конденсаторов; б) от 40 до 80 конденсаторов. Дан ряд распределения случайной величины Х.
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;
xi | 2 | 4 | 6 | 7 |
pi | 0,3 | 0,3 | 0,1 | * |
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
xi | -1 | 0 | 2 | 4 |
pi | 0,2 | 0,1 | 0,2 | 0,5 |
yi | -1 | 0 | 1 | 2 |
pi | 0,2 | 0,2 | 0,5 | 0,1 |
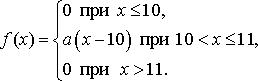
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
