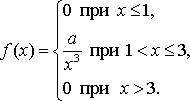Вариант 26
А). Сколько перестановок можно получить из букв слова МЕГАФОН?
Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
А). Сколько перестановок можно получить из цифр числа5867496847?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
Из букв слова ПИГМЕНТ составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?
Решить уравнение 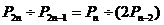 Из 12 студентов 8 имеют спортивные разряды. Найти вероятность того, что среди выбранных наудачу 5 студентов спортивный разряд имеют а)3 человека; б) менее трех человек. Незнайка и Пончик договорились встретиться у фонтана между 10 и 11 часами утра. Каждый из них может прийти к фонтану в любой промежуток времени от 10 до 11 часами утра. Определить вероятность того, что время ожидания одним другого будет не больше 15 минут. Среди населения 33,7% имеют первую 37,5% —- вторую, 20,9%—третью и 7,9% — четвертую группу крови, а) Найдите вероятность того, что случайно взятому больному можно перелить кровь случайно взятого донора, б) Найдите вероятность того, что переливание крови можно осуществить, если имеются 2 донора. Баскетболист делает 8 бросков мячом в корзину. Вероятность попадания мяча при каждом броске одинакова и равна 0,4. найти вероятность того, что а) баскетболист ровно 4 раза попадет мячом в корзину; б) попаданий в корзину будет менее пяти в) попаданий мячом будет не более 5. Завод отправил партию консервов в 2000 штук. Вероятность того, что консервная банка будет разгерметизирована, равна 0,0035. Какова вероятность того, что разгерметизировано будет не более 4 банок консервов? При штамповке металлических клемм получается в среднем 80% годных. Найдите вероятность того, что среди 900 клемм окажется а) 750 годных; б) от 700 до 820 годных. Дан ряд распределения случайной величины Х.
Из 12 студентов 8 имеют спортивные разряды. Найти вероятность того, что среди выбранных наудачу 5 студентов спортивный разряд имеют а)3 человека; б) менее трех человек. Незнайка и Пончик договорились встретиться у фонтана между 10 и 11 часами утра. Каждый из них может прийти к фонтану в любой промежуток времени от 10 до 11 часами утра. Определить вероятность того, что время ожидания одним другого будет не больше 15 минут. Среди населения 33,7% имеют первую 37,5% —- вторую, 20,9%—третью и 7,9% — четвертую группу крови, а) Найдите вероятность того, что случайно взятому больному можно перелить кровь случайно взятого донора, б) Найдите вероятность того, что переливание крови можно осуществить, если имеются 2 донора. Баскетболист делает 8 бросков мячом в корзину. Вероятность попадания мяча при каждом броске одинакова и равна 0,4. найти вероятность того, что а) баскетболист ровно 4 раза попадет мячом в корзину; б) попаданий в корзину будет менее пяти в) попаданий мячом будет не более 5. Завод отправил партию консервов в 2000 штук. Вероятность того, что консервная банка будет разгерметизирована, равна 0,0035. Какова вероятность того, что разгерметизировано будет не более 4 банок консервов? При штамповке металлических клемм получается в среднем 80% годных. Найдите вероятность того, что среди 900 клемм окажется а) 750 годных; б) от 700 до 820 годных. Дан ряд распределения случайной величины Х.
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;
xi
| 0
| 3
| 6
| 7
|
pi
| 0,1
| *
| 0,15
| 0,3
|
Даны законы распределения двух случайных величин Х и Y:
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY. xi
| 0
| 1
| 2
| 4
|
pi
| 0,1
| 0,1
| 0,3
| 0,5
|
yi
| -2
| 0
| 2
| 4
|
pi
| 0,1
| 0,2
| 0,1
| 0,6
|
Случайная величина Х задана функцией плотности распределения 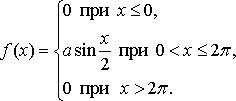
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 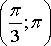 . Постройте графики функций распределения и плотности распределения.
. Постройте графики функций распределения и плотности распределения.
Вариант 27
А). Сколько перестановок можно получить из букв слова МАЙОНЕЗ?
Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
А). Сколько перестановок можно получить из цифр числа 4857364585?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
Из букв слова ПЕЧНИК составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?
Решить уравнение 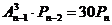 В лотерее «Спортлото 5 из 35» участник лотереи, правильно угадавший 4 или 5 видов спорта из 35 , получает денежный приз. Найти вероятность того, что данный участник угадает а) 5 видов спорта; б) получит денежный приз. Лиса Алиса и Кот Базилио договорились встретиться на Поле Чудес в Стране Дураков между 11 и 12 часами ночи. Каждый из них может прийти к месту встречи в любой промежуток времени от 10 до 11 часов ночи. Определить вероятность того, что время ожидания одним другого будет не больше 20 минут. На 3 дочерей — Алису, Марину и Елену — в семье возложена обязанность мыть посуду. Поскольку Алиса старшая, ей приходится выполнять 40% всей работы. Остальные 60% работы Марина и Елена делят поровну. Когда Алиса моет посуду, вероятность для нее разбить по крайней мере одну тарелку равна 0,02. Для Марины и Елены эта вероятность равна соответственно 0,03 и 0,04. Родители не знают, кто мыл посуду вечером, но они слышали звон разбитой тарелки. Какова вероятность того, что посуду мыла Елена? Среди коконов некоторой партии 40% цветных. Какова вероятность того, что среди 10 отобранных коконов а) цветных будет 3 кокона; б) цветных коконов будет не менее трех; в) цветных коконов будет не более 9. Вероятность попадания в цель при каждом выстреле равна 0,001. Найдите вероятность попадания в цель двумя и более выстрелами при залпе из 3000 орудий. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение минуты равна 0,002. Найти вероятность того, что в течение минуты обрыв произойдет на а) трех веретенах; б) от 13 до 40 веретенах. Дан ряд распределения случайной величины Х.
В лотерее «Спортлото 5 из 35» участник лотереи, правильно угадавший 4 или 5 видов спорта из 35 , получает денежный приз. Найти вероятность того, что данный участник угадает а) 5 видов спорта; б) получит денежный приз. Лиса Алиса и Кот Базилио договорились встретиться на Поле Чудес в Стране Дураков между 11 и 12 часами ночи. Каждый из них может прийти к месту встречи в любой промежуток времени от 10 до 11 часов ночи. Определить вероятность того, что время ожидания одним другого будет не больше 20 минут. На 3 дочерей — Алису, Марину и Елену — в семье возложена обязанность мыть посуду. Поскольку Алиса старшая, ей приходится выполнять 40% всей работы. Остальные 60% работы Марина и Елена делят поровну. Когда Алиса моет посуду, вероятность для нее разбить по крайней мере одну тарелку равна 0,02. Для Марины и Елены эта вероятность равна соответственно 0,03 и 0,04. Родители не знают, кто мыл посуду вечером, но они слышали звон разбитой тарелки. Какова вероятность того, что посуду мыла Елена? Среди коконов некоторой партии 40% цветных. Какова вероятность того, что среди 10 отобранных коконов а) цветных будет 3 кокона; б) цветных коконов будет не менее трех; в) цветных коконов будет не более 9. Вероятность попадания в цель при каждом выстреле равна 0,001. Найдите вероятность попадания в цель двумя и более выстрелами при залпе из 3000 орудий. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение минуты равна 0,002. Найти вероятность того, что в течение минуты обрыв произойдет на а) трех веретенах; б) от 13 до 40 веретенах. Дан ряд распределения случайной величины Х.
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;
xi
| 1
| 2
| 4
| 7
|
pi
| 0,1
| 0,2
| 0,1
| *
|
Даны законы распределения двух случайных величин Х и Y:
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY. xi
| -4
| 0
| 1
| 2
|
pi
| 0,2
| 0,1
| 0,2
| 0,5
|
yi
| -1
| 0
| 2
| 4
|
pi
| 0,2
| 0,2
| 0,5
| 0,1
|
Случайная величина Х задана функцией плотности распределения 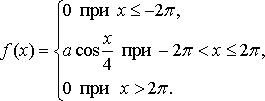
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 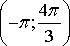 . Постройте графики функций распределения и плотности распределения.
. Постройте графики функций распределения и плотности распределения.
Вариант 28
А). Сколько перестановок можно получить из букв слова КУПОЛ?
Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
А). Сколько перестановок можно получить из цифр числа 12343263429?
Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
Из букв слова ПЛАНШЕТ составляются пятибуквенные слова.
А).Сколько таких слов можно получить?
Б) Сколько таких слов начинается с буквы П?
В) А если слова содержат не менее 5 букв?
Решить уравнение 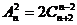 В аудитории находятся 25 студентов. 10 из них изучают английский язык, а остальные 15 – французский. Случайным образом для уборки территории отбираются 7 студентов. Найти вероятность того, что среди них а) ровно 3 изучают английский язык; б) студентов изучающих французский больше. Улитка переползает тропинку за 9 минут. Какова вероятность того, что улитка заметит ползущего по тропинке жука, если она может это сделать лишь в том случае, когда жук находится не более чем в трех минутах до пересечения курса улитки, или не более чем в трех минутах после пересечения жуком курса улитки. Курс жука перпендикулярен курсу улитки. Агентство по страхованию автомобилей разделяет водителей по 3 классам: класс Н1 (мало рискует), класс H2 (рискует средне), класс H3 (рискует сильно). Агентство предполагает, что из всех водителей, застраховавших автомобили, 30% принадлежат к классу 50% — к классу H2 и 20% — к классу H3. Вероятность того, что в течение года водитель класса Н1 попадет хотя бы в одну аварию, равна 0,01, для водителя класса H2 эта вероятность равна 0,02, а для водителя класса H3 — 0,08. Водитель А страхует свою машину и в течение года попадает в аварию. Какова вероятность того, что он относится к классу H3? По каналу связи передается 8 сообщений. Каждое из них независимо от других с вероятностью 0,1 искажается помехами. Найти вероятности следующих событий: а) из 8 событий ровно 5 искажаются помехами; б) искажаются помехами не более половины всех передаваемых сообщений; в) помехами искажается более 5 сообщений. При изготовлении радиоламп в среднем бывает 2% брака. Найдите вероятность того, что в партии из 200 ламп не более двух бракованных. Коммутатор учреждения обслуживает в среднем 100 абонентов. Вероятность того, что в течение одной минуты абонент позвонит на коммутатор, равна 0,04. Какова вероятность того, что в течение минуты на коммутатор позвонит а)12 абонентов; б) от 20 до 40 абонентов. Дан ряд распределения случайной величины Х.
В аудитории находятся 25 студентов. 10 из них изучают английский язык, а остальные 15 – французский. Случайным образом для уборки территории отбираются 7 студентов. Найти вероятность того, что среди них а) ровно 3 изучают английский язык; б) студентов изучающих французский больше. Улитка переползает тропинку за 9 минут. Какова вероятность того, что улитка заметит ползущего по тропинке жука, если она может это сделать лишь в том случае, когда жук находится не более чем в трех минутах до пересечения курса улитки, или не более чем в трех минутах после пересечения жуком курса улитки. Курс жука перпендикулярен курсу улитки. Агентство по страхованию автомобилей разделяет водителей по 3 классам: класс Н1 (мало рискует), класс H2 (рискует средне), класс H3 (рискует сильно). Агентство предполагает, что из всех водителей, застраховавших автомобили, 30% принадлежат к классу 50% — к классу H2 и 20% — к классу H3. Вероятность того, что в течение года водитель класса Н1 попадет хотя бы в одну аварию, равна 0,01, для водителя класса H2 эта вероятность равна 0,02, а для водителя класса H3 — 0,08. Водитель А страхует свою машину и в течение года попадает в аварию. Какова вероятность того, что он относится к классу H3? По каналу связи передается 8 сообщений. Каждое из них независимо от других с вероятностью 0,1 искажается помехами. Найти вероятности следующих событий: а) из 8 событий ровно 5 искажаются помехами; б) искажаются помехами не более половины всех передаваемых сообщений; в) помехами искажается более 5 сообщений. При изготовлении радиоламп в среднем бывает 2% брака. Найдите вероятность того, что в партии из 200 ламп не более двух бракованных. Коммутатор учреждения обслуживает в среднем 100 абонентов. Вероятность того, что в течение одной минуты абонент позвонит на коммутатор, равна 0,04. Какова вероятность того, что в течение минуты на коммутатор позвонит а)12 абонентов; б) от 20 до 40 абонентов. Дан ряд распределения случайной величины Х.
а)Найти значение *;
б) изобразить полигон распределения;
в) найти и изобразить графически функцию распределения;
г )найти вероятность того, что случайная величина Х примет значение в интервале
[3,5; 7,5);
д) Найти вероятность того, что случайная величина не попадет в интервал
[3,5; 7,5);
е) найти математическое ожидание случайной величины Х;
ж) найти дисперсию случайной величины Х;
xi
| 2
| 4
| 6
| 7
|
pi
| 0,45
| 0,3
| 0,1
| *
|
Даны законы распределения двух случайных величин Х и Y:
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY. xi
| -1
| 0
| 1
| 4
|
pi
| 0,4
| 0,1
| 0,3
| 0,2
|
yi
| -4
| 0
| 1
| 2
|
pi
| 0,1
| 0,3
| 0,1
| 0,5
|
Случайная величина Х задана функцией плотности распределения 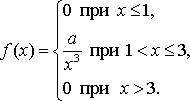
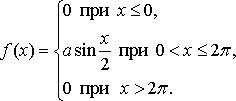
![]() . Постройте графики функций распределения и плотности распределения.
. Постройте графики функций распределения и плотности распределения.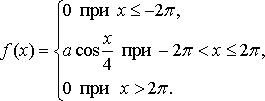
![]() . Постройте графики функций распределения и плотности распределения.
. Постройте графики функций распределения и плотности распределения.