Свойства функции распределения.
1. 
.
2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси.
3. 
, 
.
4. Р(х1
Х<x2)=F(x2)-F(x1). (4)
Пример: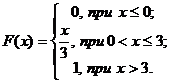 
Найти вероятность того, что случайная величина Х примет значение в интервале [2; 5).
Решение: По формуле Р(х1Х<x2)=F(x2)-F(x1). (4)
Р(2Х<5)=F(5)-F(2)=1-2/3=1/3. (4).
Ответ : 1/3.
Математические операции над случайными величинами.
Определение: Случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какое значение принимает другая случайная величина. В противном случае случайные величины называются зависимыми.
Пример: Суммы выигрыша в двух различных лотереях – независимые случайные величины так как при любом выигрыше в первой лотерее, закон распределения выигрышей по второй лотерее не изменится.
Определим математические операции над дискретными случайными величинами.
Пусть даны две случайные величины: Х и Y
xi | х1 | х2 | х3 | ….. | xn |
pi | p1 | p2 | p3 | ….. | pn |
yj | y1 | y2 | y3 | ….. | ym |
pj | p1 | p2 | p3 | ….. | pm |
Замечание: так как в ряде случаев одни и те же значения xim могут получаться одними и теми же способами при различных xi, то вероятности таких повторяющихся значений находятся сложением исходных вероятностей.
Пример: Дана случайная величина Х:
xi | -3 | -2 | 0 | 1 | 2 |
pi | 0,1 | 0,2 | 0,05 | 0,3 | 0,35 |
Найти закон распределения случайных величин 5Х и Х2.
Решение: Закон распределения случайной величины 5X.
5xi | -15 | -10 | 0 | 5 | 10 |
pi | 0,1 | 0,2 | 0,05 | 0,3 | 0,35 |
Случайная величина Х2 примет значения (-3)2=9; (-2)2=4; (0)2=0; 12=1 и 22=4.
Значение Х=4 получили при значении х=-2 с вероятностью 0,2 и при значении х=2 с вероятностью 0,45. Тогда Р(Х2=4)=0,2+0,35=0,55.
Закон распределения случайной величины X2.
Xi2 | 0 | 1 | 4 | 9 |
pi | 0,05 | 0,3 | 0,55 | 0,1 |
3. Суммой (разностью или произведением) случайных величин Х и Y называется случайная величина, которая принимает все возможные значения вида хi+yj (хi-yj или хiyj), где i=1, 2,…, n, j=1, …, m с вероятностями pij=Р
. Если случайные величины независимы, то по теореме умножения вероятностей
pij=Р
(5)
Замечание: так как в ряде случаев одни и те же значения хi+yj (хi-yj или хiyj), могут получаться одними и теми же способами при различных xi, yj то вероятности таких повторяющихся значений находятся сложением исходных вероятностей pi или pij .
Пример: Даны законы распределения двух случайных величин Х и Y:
xi | -2 | 0 | 1 | 2 |
pi | 0,2 | 0,1 | 0,3 | 0,4 |
yi | -2 | 0 | 1 | 4 |
pi | 0,1 | 0,2 | 0,1 | 0,6 |
Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
Решение: Составим вспомогательную таблицу:
X+Y | yj | -2 | 0 | 1 | 4 |
xi | pi pj | 0,1 | 0,2 | 0,1 | 0,6 |
-2 | 0,2 | -4 0,02 | -2 0,04 | -1 0,02 | 2 0,12 |
0 | 0,1 | -2 0,01 | 0 0,02 | 1 0,01 | 4 0,06 |
1 | 0,3 | -1 0,03 | 1 0,06 | 2 0,03 | 5 0,18 |
2 | 0,4 | 0 0,04 | 2 0,08 | 3 0,04 | 6 0,24 |
Таблица заполняется следующим образом: в каждой клетке таблицы в левом углу находится значение разности хi-yj, а в правом углу – вероятности этих значений, полученные в результате перемножения вероятностей pi и pj.
Так как среди 16 значений таблицы находятся повторяющиеся, то соответствующие вероятности их складываем по теореме сложения вероятностей. Например, значение
Z=X+Y=0 может быть получено, когда X=2, Y=-2 с вероятностью 0,04; Х=0,Y=0 с вероятностью 0,02, поэтому Р(Z=0)=0,04+0,02=0,06 и т. д.
zi | -4 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
pi | 0,02 | 0,05 | 0,05 | 0,06 | 0,07 | 0,23 | 0,04 | 0,06 | 0,18 | 0,24 |
Убедимся, что условие 
выполнено.
Б) аналогично составляем таблицу для U=XY
XY | yj | -2 | 0 | 1 | 4 |
xi | pi pj | 0,1 | 0,2 | 0,1 | 0,6 |
-2 | 0,2 | 4 0,02 | 0 0,04 | -2 0,02 | -8 0,12 |
0 | 0,1 | 0 0,01 | 0 0,02 | 0 0,01 | 0 0,06 |
1 | 0,3 | -2 0,03 | 0 0,06 | 1 0,03 | 4 0,18 |
2 | 0,4 | -4 0,04 | 0 0,08 | 2 0,04 | 8 0,24 |
ui | -8 | -4 | -2 | 0 | 1 | 2 | 4 | 8 |
pi | 0,12 | 0,04 | 0,05 | 0,28 | 0,03 | 0,07 | 0,2 | 0,24 |
Числовые характеристики дискретных случайных величин
Закон распределения полностью характеризует дискретную случайную величину. Однако, когда невозможно определить закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины:
Математическое ожидание,
Дисперсия,
Среднее квадратичное отклонение
Эти величины определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения.
Математическое ожидание M дискретной случайной величины - это среднее значение случайной величины, равное сумме произведений всех возможных значений случайной величины на их вероятности.
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно самой постоянной.
2. Постоянный множитель можно выносить за знак математического ожидания.
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
