«Статистика» (стр. 9 )

Определить средний % влажности, дисперсию, среднее квадратическое отклонение, с вероятностью 0,954 возможные пределы, в которых ожидается ср. % влажности всей готовой продукции, с вероятность 0,987 возможные пределы удельного веса стандартной продукции при условии, что к нестандартной партии относятся изделия с влажностью до 13 и выше 19 %.

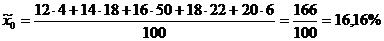
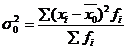
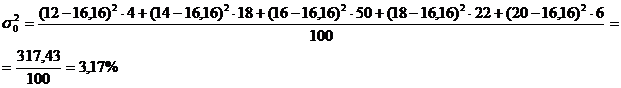
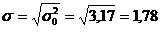
Лишь с определенной вероятностью можно утверждать, что генеральная доля от выборочной доли и генеральная средняя от выборочной средней, отклоняются в t раз.

В статистике эти отклонения называются предельными ошибками выборки и обозначаются .

Вероятность суждений можно повысить или понизить в t раз. При вероятности 0,683 , при 0,954, при 0,987, тогда показатели генеральной совокупности по показателям выборки определяются:

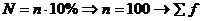
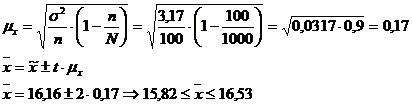
Средний процент влажности генеральной совокупности может быть любым значением, находящемся в пределах от 15,82 до 16,33.

;

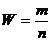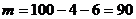
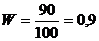
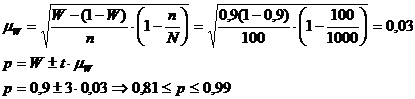
Таким образом, удельный вес стандартных изделий в генеральной совокупности находится в пределах 81 % – 99 %.

Из расчета задачи видно, что возможные пределы удельного веса единиц генеральной совокупности будут находиться:

А среднее значение генеральной совокупности находится в пределах :

Тема 8. Способы формирования выборочных с совокупностей

1. Районированный и нерайонированный отбор.

Формирование выборочной совокупности происходит из единиц генеральной совокупности, причем, отбор может быть нескольких видов:

-  нерайонированный отбор – отбор единиц в выборочную совокупность из генеральной совокупности не разбитой на группы по каким-либо признакам;

-  районированный – генеральная совокупность делится на группы по признакам.

Пример, отбор предприятий по отраслям. Разбивка генеральной совокупности на группы происходит по реально существующим признакам, в данном случае такой отбор называется типическим.

Типический отбор облегчает формирование выборочных совокупностей и обеспечивает более равномерное распределение единиц в генеральной совокупности.

При типическом отборе показатели выборочной характеристики, более точнее, чем при нерайонированном отборе.

2. Собственно-случайный отбор.

Дает лотерея, жеребьевка или тираж, при этом обеспечивается абсолютно равная возможность попадания в выборку любой единицы.

Пример, тираж «Русское лото» и попадание в выборку любого билета, при этом ошибка выборки определяется по формуле:

3. Механический отбор.

Составляют список всех единиц совокупности и определяют интервал путем деления числа генеральной совокупности на число выборочной совокупности.

Поэтому в выборочную совокупность войдут единицы генеральной совокупности, расположенные в списке через данный интервал.

Принцип случайного отбора в механической выборке обеспечивается тем, что единицы в генеральной совокупности располагаются в таком порядке, который не оказывает влияние на изучаемый признак или фактор. Механический отбор можно использовать и без применения списков, а брать единицы так, как они располагаются в генеральной совокупности.

Пример, при 2 % отборе из 100 единиц в выборку попадает каждый 50-й. Ошибка выборки при механическом отборе, рассчитывается исходя их внутригрупповой дисперсии или средней из групповых дисперсий.

Однако, если генеральная совокупность разбита на группы по строго нейтральному признаку, то ошибку выборки, исходя из внутригрупповой дисперсии, определить нельзя, т. к. внутригрупповая равна общей дисперсии.

4. Типический отбор.

Данный отбор состоит из 2 этапов:

-  определяют признак, по которому проводится районирование генеральной совокупности;

-  в группах проводят механический отбор единиц выборочной совокупности.

При этом ошибка выборки рассчитывается:

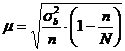
где исходя из закона сложения дисперсии равна разности общей дисперсии и межгрупповой дисперсии, т. е.

С помощью корреляционного отношения, которое определяется как корень квадратный из частного межгруппового и общей дисперсией:

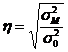
В связи с этим, дисперсия выборочной средней в типической выборке равна:

Следовательно, типизация уменьшает ошибку выборки на

Численность единиц выборочной совокупности между группами обычно распределяется пропорционально численности по группам единиц в генеральной совокупности в группах на соответствующие групповые средние квадратические отклонения.

Разновидностью типической выборки является систематический отбор, т. е. механический отбор из совокупности ранжированной по какому-либо признаку, связанному с изучаемым признаком.

Пример, отбор рабочих по семейному бюджету, связанному с их средней заработной платой.

5. Многоступенчатая выборка.

Типичный отбор состоит в многоступенчатой выборке из сочетания нескольких стадий отбора, причем на каждой стадии имеется своя единица отбора (отрасль предприятия, численность и средняя заработная плата.).

Пример, проведем многоступенчатую выборку. В области имеются 13 предприятий общей численностью 40 тыс. человек. Требуется 200 человек так, чтобы с каждого предприятия было 25 работников с различным уровнем заработной платы.

I ступень.

Определим число предприятий, попадающих в выборку: предприятий.

Для того, чтобы приступить к отбору предприятий, определим величину интервала

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22