«Статистика» (стр. 10 )

Каждый 5000-ый работник попадает в выборку:

II ступень.

Проверяем репрезитивность средней заработной платы. по всем предприятиям:

Выборочные данные репрезитивны, т. к. выборочная средняя ненамного отличается от общей средней.

III ступень.

Определим рабочих внутри предприятия. Рабочих делят на квалифицированных и неквалифицированных. Так по данным 1-го предприятия из 6800 человек 5440 являются квалифицированными, значит, 4/5 квалифицированные, а 1/5 – неквалифицированные, т. е. из 25 рабочих 20 войдут в первую группу, пять во вторую. Далее составляют 2 списка по квалификациям и определяют интервал внутри каждого списка:

Таким образом, 272-ой рабочий по списку войдет в выборку.

Далее по другим предприятиям аналогично. Из этого видно, что предприятия в пределах отрасли отбирают механическим отбором с последующей проверкой репрезитивности по среднему уровню заработной платы.

Рабочих же выбирают на основе пропорционально типическому отбору. Многоступенчатый отбор принимают при наличии нескольких типов единиц отбора, которые отличаются по своим масштабам, при этом необходимо так организовать выборочное исследование, чтобы оно равномерно распределялось между отдельными частями сложного явления.

6. Многофазная выборка.

Отличается от многоступенчатой тем, что на всех ступенях обследуется одна и та же единица отбора (обследование крестьянских хозяйств, где более полно обследуется каждое 3-е, 9-е, 27-е и т. д. хозяйство, при этом ошибка выборки незначительна и выборочные показатели более точно характеризуют генеральную совокупность).

7. Комбинирование выборочного наблюдения со сплошным.

Характерно для многофазной выборки. Оно позволяет проверить более точно типичность выборочных данных по отношению к генеральным характеристикам. Выборочные показатели сопоставляются с данными сплошного наблюдения.

8. Серийная выборка.

Если в выборку попадают не отдельные единицы совокупности, а целые серии, такая выборка называется серийная.

Пример, при 10 % обследовании качества продукции можно проверять каждую 10-ю единицу (механический отбор), при серийном – через 9 часов каждый 10-й час обследуется вся выпущенная продукция в течении целого часа.

Серийный отбор применяется редко, т. к. дает высокую ошибку выборки.

9. Моментная выборка.

На определенные моменты времени фиксируется наличие отдельных элементов изучаемого процесса.

Пример, изучение использования работниками рабочего времени и времени работы оборудования.

Моментное наблюдение охватывает все единицы совокупности, поэтому является сплошным. Цель – на основе выборочных характеристик дать репрезентативную оценку всей генеральной совокупности. Т. к. при моментном наблюдении обычно характеризуется альтернативный признак (работа или простой), то оценка репрезентативности проводится по формулам средней и предельной ошибки выборки. При этом, в качестве численности выборочной совокупности, принимается число записей моментного обследования.

Пример, в цехе работает 20 станков. За 8-ми часовую смену каждые полчаса проводились моментные обследования. Определить в каких пределах будет находиться доля работающих станков за все время смены, если в 32 случаях замечен простой, вероятность 0,954.

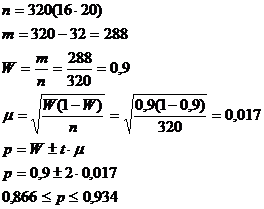
10. Малая выборка.

Такое выборочное наблюдение, численность единиц которого не более 20. Хотя общий принцип выборочного наблюдения – чем больше выборочная совокупность, тем точнее показатели, иногда используют малую выборку.

Малая выборка применяется при обследовании качества продукции с последующим уничтожением проверяемой единицы.

Средняя ошибка малой выборки определяется по формуле:

Причем, малая выборочная дисперсия рассчитывается:

Следовательно, предельная ошибка выборки:

Но в данном случае коэффициент доверия – t отличен от применяемого t в других выборочных наблюдениях. Он зависит от n (числа выборки), при увеличении n распределение стремится к нормальному и при n = 20 мало чем отличается от нормального. Если n = 20; t = 1 вероятность = 0,683.

t = 2 0,954

t = 3 0,997

11. Проверка типичности выборочных данных.

Кроме вероятностной оценки репрезентативности выборочных данных путем расчета средней и предельной ошибки выборки по каждому показателю проверка типичности часто осуществляется путем сопоставления выборочных данных с данными сплошного отбора.

Пример, обследование уровней заработной платы. Типичность отобранных предприятий проверяется путем сравнения средней заработной платы на отобранных предприятиях со средней заработной платой всех предприятий.

Существует 2 способа распространения данных выборочного наблюдения:

- способ прямого пересчета

пример, надой с одной коровы за год составил 2500 л. Среднее поголовье коров в частном владении 10000 голов. Ошибка выборки составляет 20 л. Определить годовой надой со всего поголовья имеющихся у селян:

Способом прямого пересчета можно распространять данные выборочного наблюдения на основе соотношения численности выборочной и генеральной совокупности.

Пример, при выборочном 3 % обследовании качества продукции в выборку попало 1000 единиц, из которых качество 20 не соответствует стандарту. Ошибка выборки = 2 единицы. Используя соотношение численности можно рассчитать, что число некачественных единиц из 20000 будет равно:

от 360 до 440

- способ коэффициентов, применяют при проведении выборочного наблюдения для проверки и уточнения данных сплошного обследования.

Сопоставляя выборочные данные с данными сплошного наблюдения, определяют поправочный коэффициент, а с его помощью вносят поправки в данные выборочной совокупности.

Тема 9. Ряды динамики

1. Понятие и виды рядов динамики.

Статистика рассматривает общественные явления в непрерывном развитии.

Ряд динамики – последовательно расположенные в хронологическом порядке показатели, характеризующие общественные явления и процессы в развитии. В ряду динамики для каждого отрезка времени приводится два показателя:

-  показатель времени

-  показатель уровня ряда (у).

Кроме них могут также показываться производные.

Исследование рядов динамики дает возможность показать развитие явления во времени, тенденции развития, темпы роста, основные пути развития. Ряды динамики могут состоять из - абсолютных;

- относительных;

- средних величин.

Примером ряда динамики средних величин является урожайность культур по хозяйствам области; ср. производительности.

Примером ряда динамики относительных величин может быть ряд, характеризующий темпы роста производства продукции.

Ряд динамики абсолютных величин характеризует уровни развития общественных явлений, либо на определенные моменты времени, либо за определенные промежутки времени. В зависимости от этого ряды динамики делят на:

-  интервальные;

-  моментные.

Разница между ними заключается в том, что в моментном ряду интервал – это промежуток времени между датами, а в интервальном – это промежуток времени, за который обобщены приводимые сведения.

На основе ряда динамики абсолютных величин могут быть получены ряды динамики относительных и средних величин.

2. Сопоставимость уровней ряда динамики.

Анализировать ряды динамики нельзя, если приводятся несопоставимые данные. Несопоставимость статистических данных во времени может быть вызвана следующими причинами:

1.  инфляционным процессом;

2.  территориальные изменения;

3.  изменения единиц счета;

4.  изменения курса валют;

5.  изменения степени охвата статистического наблюдения;

6.  несовершенство методологии статистического наблюдения.

Для того, чтобы привести уровни ряда в ряду динамики к сопоставимым уровням ряда необходимо провести смыкание рядов динамики.

Это можно сделать лишь в том случае, если один из уровней ряда имеется в старом и новом исчислении.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22