; постоянное число 68,30

 

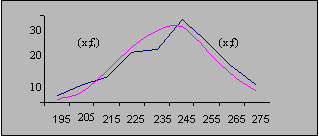Рис. 6. Кривые фактического и нормального распределения

Критерии согласия.

Математическая статистика дает несколько показателей, по которым можно судить, на сколько фактическое распределение согласуется с нормальным. Эти показатели называются критерии согласия.

Критерий согласия Колмагорова (критерий ) определяется путем деления max разности коммулятивных частот на корень квадратный из числа наблюдений:

, где d – максимальное отклонение фактической частоты от фактической частоты;

n – число наблюдений.

По приведенному примеру критерий =

По специальной таблице вероятности для критерия согласия определяют, что значение =0,59 соответствует вероятности 0,88. Это значит, что с вероятностью 0,88 можно судить об отклонении фактических частот от теоретических, которые являются случайными.

10. Асимметрия распределения и эксцесс.

Эксцесс – высоковершинность или низковершинность фактической кривой распределения по сравнению с нормальным распределением.

Высоковершинность означает положительный эксцесс и характеризуется скоплением частот в середине.

В симметричном распределении средняя арифметическая равна моде и медиане, если этого равенства нет, то распределение считают асимметричным.

Низковершинность означает отрицательный эксцесс и характеризуется большой разбросанностью частот ряда.

Коэффициент асимметрии – отношение разности между средним значением и моды и среднему квадратическому отклонению.

При симметричном отклонении разница между ср. значением и модой будет равно 0, тогда и коэффициент будет равен 0.

Если 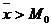, то и кривая распределения будет правосторонняя, если 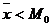, то и кривая распределения будет левосторонняя.

Пример.

Проверить по критерию согласия Колмагорова соответствие рядов распределения нормальному распределению по данным таблицы.

% выполнения норм выработки

Число рабочих

90-100

10

100-110

100

110-120

130

120-130

60

> 130

20

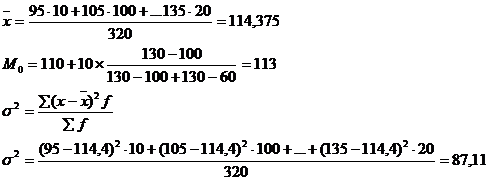
Коэффициент асимметрии равен (114,375-113)/87,11=0,0158

Тема 7. Выборочное наблюдение

1. Понятие выборочного наблюдения.

Выборочным называется такое наблюдение, при котором характеристика всей совокупности единиц дается по некоторой их части, отобранной в случайном порядке.

Выборочное наблюдение относится к несплошному наблюдению. В практике выборочное наблюдение используется для контроля качества продукции, контроля за использованием рабочего времени, контроля за выполнением норм выработки и т. д. Широкое распространение выборочное наблюдение получило в связи с тем, что затраты не его проведение достаточно меньшие, чем на проведение сплошного наблюдения, и нередко выборочное наблюдение является единственно возможным.

Например, проверка качества.

Выборочное наблюдение дает возможность получить обобщающие показатели, правильно характеризующие всю совокупность, не исследуя совокупность в целом.

Подлежащая изучению совокупность называется генеральной, а отобранная для наблюдения ее часть – выборочной (выборкой). Значение выборочного наблюдения в том, что данный метод повышает оперативность и уменьшает ошибки. Поскольку данная совокупность состоит из единиц с изменяющимися признаками. То состав выборки может отличаться от генеральной совокупности.

В генеральной совокупности доля единиц, обладающих изучаемым признаком, называется генеральной долей и обозначается Р, а средняя генеральная средней - .

В выборке доля изучаемого признака называется выборочной долей и обозначается W. А средняя выборочная средней - .

Частость определяется как отношение единиц, обладающих изучаемым признаком ( ), к общей численности единиц выборочной совокупности (п).

2. Понятие и расчет ошибки выборки.

Задачей выборочного наблюдения является дача верных представлений о сводных показателях всей совокупности на основе некоторой их части, подвергнутой наблюдению. Возможное отклонение выборочной доли и выборочной средней от доли и средней в генеральной совокупности называется ошибкой выборки или ошибкой репрезентативности. Чем больше величина этой ошибки, тем больше показатели выборочного наблюдения отличаются от показателей генеральной совокупности.

Различаются:

-  ошибки выборки;

-  ошибки регистрации.

Ошибки регистрации возникают при неправильном установлении факта в процессе наблюдения. Они свойственны как сплошному наблюдению, так и выборочному, но в выборочном их меньше.

По природе ошибки бывают:

-  тенденциозные – преднамеренные, т. е. были отобраны либо лучшие, либо худшие единицы совокупности. При этом наблюдения теряют смысл;

-  случайные – основной организационный принцип выборочного наблюдения состоит в том, чтобы не допустить преднамеренного отбора, т. е. обеспечить строгое соблюдение принципа случайного отбора.

Общим правилом случайного отбора является: у отдельных единиц генеральной совокупности должны быть совершенно одинаковые условия и возможности упасть в число единиц, входящих в выборку. Это характеризует независимость результата выборки от воли наблюдателя. Воля же наблюдателя порождает тенденциозные ошибки. Ошибка выборки при случайном отборе носит случайный характер. Она характеризует размеры отклонений генеральных характеристик от выборочных.

Формулы средней ошибки выборки.

В связи с тем, что признаки в изучаемой совокупности варьируют, то состав единиц, попавших в выборку, может не совпадать с составом единиц всей совокупности. Это означает, что Р и не совпадают с W и. Возможное расхождение между этими характеристиками определяется ошибкой выборки, которая определяется по формуле:

где - генеральная дисперсия.

где - выборочная дисперсия.

Отсюда видно, где генеральная дисперсия отличается от выборочной дисперсии в раз.

Существует повторный и бесповторный отбор. Сущность повторного отбора состоит в том, что каждая, попавшая в выборку единица, после наблюдения возвращается в генеральную совокупность и может быть исследована повторно. При повторном отборе средняя ошибка выборки рассчитывается:

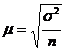
Для показателя доли альтернативного признака дисперсия выборки определяется по формуле:

На практике повторный отбор применяется редко. При бесповторном отборе, численность генеральной совокупности N в ходе выборки сокращается, формула средней ошибки выборки для количественного признака имеет вид:

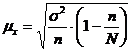, тогда

Одно из возможных значений, в которых может находиться доля изучаемого признака равно:

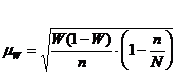
где - ошибка выборки альтернативного признака.

Пример.

При выборочном обследовании 10 % изделий партии готовой продукции по методу без повторного отбора получены следующие данные о содержании влаг в образцах.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22