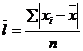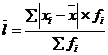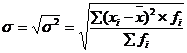«Статистика» (стр. 5 )

1 год

1.01.94  – 645 тыс. чел.,

4 .5 года

1.07.98 – 649 тыс. чел.,

0.5 года

1.01.99 – 657 тыс. чел.

Определить среднюю численность:

1. 

2.  ,

где 2 – это два полугодия;

1 – это одно.

4. Средняя квадратическая величина.

Применяется при определении показателей вариации и рассчитывается как корень квадратный из средней арифметической.

Средняя квадратическая простая:

Взвешенные: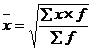

5. Средние структурные величины.

При определении среднеструктурных величин определяются мода и медиана.

Медиана – вариант, расположенный в центре ранжированного ряда, медиана делит ряд на две одинаковые части, таким образом, чтобы по обе ее стороны находилось одинаковое число единиц совокупности. Если всем единицам ряда придать порядковые номера, то порядковый номер медианы будет определяться по формуле 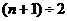для рядов, где - нечетное, если же ряд с четным числом единиц, то медианой будет являться среднее значение между двумя вариантами, определенными по формуле: .

Нахождение медианы в интервальных вариационных рядах требует предварительного определения интервала в котором находится медиана, т. е. медианного интервала – этот интервал характеризуется тем, что его коммулятивная частота равна полусумме или превышает полусумму всех частот ряда.

В зависимости от этого медиану определяют по формуле:

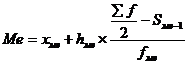
где - нижняя граница медианного интервала;

- ширина медианного интервала;

- сумма накопленных частот до частоты медианного интервала;

- частота медианного интервала.

Пример.

Определить медиану, если:

Вывод: из 1000 рабочих 500 чел. имеет стаж работы меньше 8,57.лет.

Квартиль –это четвертая часть совокупности, определяется как и медиана, только сумму частот необходимо разделить на 4, а при определении квартильного интервала коммулятивная частота должна быть больше или равна четверти суммы частот совокупности.

Мода – вариант наиболее часто встречающийся в совокупности. В дискретном ряду мода – это вариант с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант модального интервала. В пределах интервала надо определить то значение признака, который обладает наибольшей частотой. Определяем по формуле:

где - нижний уровень модального интервала;

- ширина интервала;

- частота интервала;

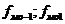- частота предыдущего и последующего интервала.

Дециль – делит совокупность на десять равных частей. Определяется аналогично как и квартиль только сумму частот необходимо разделить на 10.

5.  Средняя геометрическая.

Применяется для характеристики рядов динамики при определении средних темпов роста.

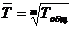, если 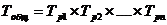, тогда:

;

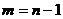, т. е. число уровней ряда без одного или число темпов роста.,

- начальный уровень ряда;

- конечный уровень ряда.

Пример.

Определить цепные темпы роста и средний темп роста товарной продукции, если:

; ; ;

средний темп роста = = 1,0153

Это изменение возникает в результате того, что индивидуальные значения складываются по совокупным факторам, которые по-разному действуют на совокупность целого.

Средняя величина – это абстрактная обобщающая характеристика признака изучаемой совокупности.

Она не дает данные о том, как отдельные значения изучаемой совокупности группируются вокруг средней.

Колеблимость отдельных значений характеризуют показатели вариации. Термин «вариация» происходит от латинского и обозначает – изменения, колеблимость.

Под вариацией в статистике понимают такие количественные изменения в пределах одного признака в однородной совокупности, которые обусловлены и зависят от влияния различных факторов.

Анализ статистической совокупности позволяет оценить степень зависимости изучаемой совокупности и ее признаков от ее факторов.

Пример.

Изучая вариацию можно определить однородность совокупности. Степень близости данных отдельных единиц x к средней измеряются рядом абсолютных, относительных и средних показателей вариации.

4. Показатели вариации.

Несгрупированый ряд Сгруппированный ряд

5-ый показатель. Коэффициент вариации – это отношение седнего квадратического отклонения к среднему значению.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22