2). 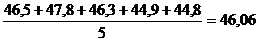 , и т. д.
, и т. д.
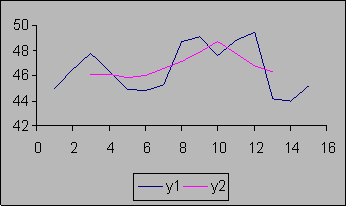 |
у1 – фактическая кривая
у2 – сглаженная
Рис. 8. Динамика выпуска продукции
Для того, чтобы сгладить ряд по 5 дням необходимо по каждым последующим 5 дням рассчитать среднюю арифметическую простую, при этом среднее число за первых 5 дней поставить на 3-ю дату, а следующие 5 дней начинать рассчитывать со 2-го числа, а результат ставить на 4-ю дату. Чем больше интервал, за который исчисляется средняя, тем больше сглаженный ряд усредняет фактический ряд, при этом теряется много информации. Чем меньше интервал, тем больше сглаженный ряд приближается к конкретному ряду. По сглаженному ряду, показанному на графике можно выявить тенденцию в развитии.
Метод аналитического выравнивания ряда динамики по прямой
Если фактические уровни ряда динамики нанести на график, то получим ломаную линию, которая будет отражать как основные тенденции в развитии, так и отклонения от них, вызванные сезонными колебаниями или другими факторами. Чтобы выявить тенденцию необходимо выровнять ломаную линию, в основе выравнивания лежит теоретический анализ сущности данного явления и законы его развития. Как известно, уравнение прямой выражается следующей формулой: ![]() , где
, где ![]() - значение уровней выровненного ряда динамики;
- значение уровней выровненного ряда динамики;
![]() - параметры прямой;
- параметры прямой;
t – показатель времени.
Следовательно, задача сводится к тому, чтобы фактические уровни ряда динамики (у) заменить теоретическими уровнями ряда (![]() ). Прямая, выравнивающая ряд должна проходить в максимальной близости от фактических уровней ряда, т. е. сумма квадратов отклонений должна быть наименьшей. Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров
). Прямая, выравнивающая ряд должна проходить в максимальной близости от фактических уровней ряда, т. е. сумма квадратов отклонений должна быть наименьшей. Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров ![]() :
:
1. 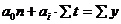
2. 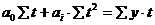
где, у – фактические уровни ряда,
n – число уровней ряда.
Для решения этого уравнения необходимо, чтобы сумма t была равна 0, для этого даты необходимо расположить так:
–7-6-5-4-3-2-1 0 +1+2+3+4+5+6+7;
![]() ,
,
тогда уравнение принимает вид:
![]()
1. 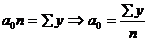
3. ![]()
Число | Фактические уровни | Условное число | Условные уровни
|
|
|
|
1 | 2010 | -7 | 10 | 49 | -14070 | 1993,76 |
2 | 2025 | -6 | 25 | 36 | -12150 | 2005,66 |
3 | 2042 | -5 | 42 | 25 | -10210 | 2017,56 |
4 | 1910 | -4 | -90 | 16 | -7640 | 2029,46 |
5 | 1960 | -3 | -40 | 9 | -5880 | 2041,36 |
6 | 2101 | -2 | 101 | 4 | -4202 | 2053,26 |
7 | 2050 | -1 | 50 | 1 | -2050 | 2065,16 |
8 | 2130 | 0 | 130 | 0 | 0 | 2077,06 |
9 | 2152 | 1 | 152 | 1 | 2152 | 2088,96 |
10 | 2103 | 2 | 103 | 4 | 4206 | 2100,86 |
11 | 2080 | 3 | 80 | 9 | 6240 | 2112,76 |
12 | 2193 | 4 | 193 | 16 | 8772 | 2124,66 |
13 | 2204 | 5 | 204 | 25 | 11020 | 2136,56 |
14 | 2230 | 6 | 230 | 36 | 13380 | 2148,46 |
15 | 1966 | 7 | -34 | 49 | 13762 | 2160,36 |
Всего: | 31156 | 280 | 3330 |
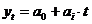
![]()

![]()
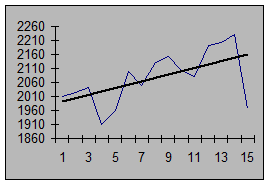 |
Рис. 9. Аналитическое выравнивание ряда динамики по прямой
6. Интерполяция и экстраполяция рядов динамики.
Выравниванием рядов динамики пользуются для того, чтобы найти значение недостающего члена ряда. Такой способ называется интерполяцией.
Экстраполяцией рядов динамики называют прием, который заключается в том, что, продолжая найденные математические кривые можно предсказать дальнейшее развитие событий. Прогнозирование базируется на знании развития прогнозируемого явления, а также факторов, влияющих на это явление и того, каким образом эти факторы могут изменить развитие явления.
7. Приемы изучения сезонных колебаний.
Сезонное колебание – это более или менее устойчивые внутригодовые колебания в ряду динамики, обусловленные специфическими условиями производства или потребления данного товара.
Сезонные колебания характеризуются индексами сезонности (JS) совокупность которых образует сезонную волну. Индекс сезонности - средняя величина, определенная из % отношений по одноименным месяцам фактических уровней ряда динамики к выровненным уровням.
Для выявления сезонных колебаний берут данные за несколько лет с распр6еделением по месяцам, это делается для того, чтобы выявить устойчивую сезонную волну, на которой бы не отражались индивидуальные факторы одного года. Определяя индексы сезонности, пользуются несколькими методами, выбор которых зависит от вида ряда:
1). Если ряд содержит определенную тенденцию в развитии, то прежде чем определить сезонную волну, определяют общую тенденцию, при этом рассчитывают % фактических данных к выровненным, а индекс сезонности по формуле:
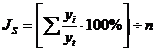
2). Если же ряд не содержит ярко выраженную тенденцию, то такой ряд называют стабильным, а индекс сезонности рассчитывают по формуле:
![]()
Пример, вычисление индексов сезонности в стабильном ряду динамики.
Месяц | Закупка молока | Месячные данные в % к среднегодовой | ||||
1995 | 1996 | 1997 | Всего за 3 года | В среднем за год | ||
Январь | 1530 | 1600 | 1760 | 4890 | 1630 | 62,8 |
Февраль | 1920 | 2440 | 2560 | 6920 | 2306,6 | 88,8 |
Март | 2740 | 3390 | 3220 | 9350 | 3116,6 | 120 |
Апрель | 3280 | 3980 | 4030 | 11290 | 3763,3 | 144,9 |
Май | 2750 | 3280 | 4000 | 10030 | 3343,3 | 128,7 |
Июнь | 3280 | 3910 | 4580 | 11770 | 3923,3 | 151 |
Июль | 2590 | 2840 | 3150 | 8580 | 2860 | 110,7 |
Август | 2140 | 2260 | 2520 | 6920 | 2306,6 | 88,8 |
Сентябрь | 2250 | 2520 | 2660 | 7430 | 2476,6 | 95,3 |
Октябрь | 1980 | 2290 | 2200 | 6470 | 2156,6 | 83 |
Ноябрь | 1490 | 1930 | 1680 | 5100 | 1700 | 65,4 |
Декабрь | 1460 | 1790 | 1510 | 4760 | 1586,6 | 61 |
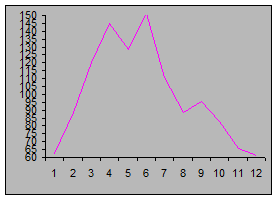 |
Рис. 10. Индекс сезонности

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |



