4. Относительные величины интенсивности – показатели, характеризующие меру распространения или развития данного явления в определенной среде, они рассчитываются как отношение абсолютной величины к размеру среды, в которой они находятся (производство сельскохозяйственной продукции с 1 га сельскохозяйственных угодий; фонд отдачи, т. е. сколько рублей товарной продукции получено на 1 рубль вложенные в основные средства).
5. Относительные величины сравнения, получаются путем сравнения одноименных уровней, относящихся к разным объектам, территориям за один и тот же период или на один и тот же момент времени (производство хлеба на вяземском заводе по сравнению с сафоновским).
Тема 6. Средние величины и Показатели вариации
1. Сущность средних величин и их значение в статистическом анализе.
Средней величиной является обобщающая характеристика большого количества индивидуальных значений варьирующего признака. Средняя величина – то общее, что характерно для всей совокупности, но исключает те отличия, которые наблюдаются у отдельных единиц как бы взаимно погашая их. Средние величины должны определятся не для всех совокупностей, а только для тех, которые являются однородными. Средние величины, полученные для неоднородных совокупностей не только не имеют ценностей, но даже могут принести вред искажая истинный характер общественного явления. Таким образом, в статистике средней величиной является обобщающий показателей, характеризующий типичный уровень варьирующего признака в расчете на единицу однородной совокупности.
Значение средней величины в следующем: их используют для оценки результатов использования научных разработок в производстве, в социальной жизни, а также в изыскании скрытых и неиспользованных резервов.
2. Виды средних величин.
1. Средняя арифметическая величина.
Самым распространенным видом расчета средней величины является определение средней арифметической.
Пример.
5 рабочих токарей делают одинаковые детали за смену: первый – 12
второй – 9
третий – 11
четвертый – 13
пятый – 15
Определить среднюю производительность.
Всего – 60.
Производительность – 12= 60/5
В этом случае производятся вычисления по формуле средней арифметической простой
![]()
где ![]() – средняя варианта;
– средняя варианта;
х – варианта;
n – число единиц совокупности несгруппированного ряда.
Данная формула применяется в том случае, если в исходных данных значение каждого варианта встречается один раз. Если же значение вариант (х) встречается по несколько раз, т. е. имеет место частота, то расчет средней арифметической производится по формуле средней арифметической взвешенной
![]()
где х – варианта;
![]() - частота.
- частота.
Пример.
Определить среднюю грузоподъемность одного крана, если имеется:
Число кранов ( | Грузоподъемность тонн (х) |
1 | 40 |
2 | 25 |
3 | 10 |
4 | 5 |
Итого 10 |
![]()
Средние арифметические применяются в тех случаях, когда общий объем варьирующего признака для всей совокупности образуется как сумма значений признаков отдельных ее единиц. При расчетах средней арифметической выделяются ее основные свойства:
- среднее от постоянной величины равна ей самой:
![]()
![]()
- произведение средней на сумму частот равно сумме произведений вариант на частоты:
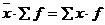
- изменение каждого варианта на одну и туже величину изменяет среднюю величину на эту же величину:
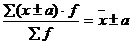
- изменение каждого варианта на одно и тоже число изменяет среднюю во столько же раз:
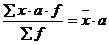
- изменение каждой частоты в одно и тоже число раз не изменяет величину средней:
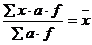
- алгебраическая сумма отклонений всех вариантов от средней равна 0:
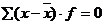
Определение средней арифметической по данным интервального вариационного ряда происходит следующим образом, – для каждого ряда определяется среднее значение интервала как полусумма его нижнего и верхнего значения вариант, а далее расчет ведется по формуле средней арифметической взвешенной.
Пример.
Распределение рабочих цеха по производительности
Производительность. шт. | Среднее значение xi | Количество рабочих fi |
0-5 | 2,5 | 146 |
5-10 | 7,5 | 495 |
10-15 | 125 | 237 |
15-20 | 17,5 | 103 |
20 и более | 22,5 | 19 |
Всего: | 1000 |
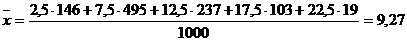 (лет)
(лет)
2. Средняя гармоническая величина.
Это величина обратная среднеарифметической. Она применяется, когда известны отдельные значения варьирующего признака и вся совокупность признаков, а частоты неизвестны.
![]()
Существует два вида среднегармонической:
Средняя гармоническая простая определяется: 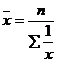
где n – число единиц совокупности для несгруппированного ряда;
![]() – варианта.
– варианта.
Пример.
Скорость по течению реки 60 км/ч., против течения – 40 км/ч. Определить среднюю скорость движения.
Весь путь S=1, но тем не менее путь проходят дважды, то S=2, V1=60 км/ч., V2=40 км/ч., тогда средняя скорость движения:
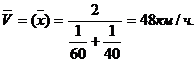
Средняя гармоническая взвешенная определяется:
![]() ;
; 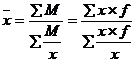
Пример.
Имеются данные о валовом сборе и урожайности зерновых культур по трем колхозам:
Колхозы | Валовый сбор | Урожайность |
1 | 1000 | 20 |
2 | 1100 | 22 |
3 | 1440 | 24 |
|
|
Определить среднюю урожайность.
Валовый сбор = урожайность ![]() площадь.
площадь.
Частота – площадь посевов
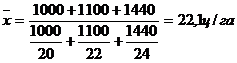
3. Средняя хронологическая величина.
Применяется для определения среднего уровня в моментных рядах динамики. Существует два вида рядов динамики:
1. моментные;
2. интервальные.
Интервальные – это такие ряды в которых данные приводятся за определенный период времени (месяц, год). Средний уровень ряда в интервальном ряду определяется по средней арифметической простой.
Моментные – это такие ряды, где данные представлены на определенный момент времени (на определенную дату). Если интервалы времени между датами равны, то расчет средней ведут по формуле средней хронологической простой.
![]()
Пример.
Моментный ряд:
1.01 | 1.02 | 1.03 | 1.04 | |
Численность рабочих | 100 | 108 | 102 | 96 |
![]() чел.
чел.
Если интервалы между датами в моментных рядах не одинаковые, то расчет ведется в два этапа: по средней хронологической взвешенной
1. определяется средняя внутри каждого интервала времени по среднеарифметической простой;
2. определяется общая средняя по среднеарифметической взвешенной, где частотами являются интервалы между датами.
Пример.
Имеются данные о численности населения города на:
1.01.93 ![]() – 632 тыс. чел.,
– 632 тыс. чел.,

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |



