Существует два вида связи между факторами и результативными признаками:
1. функциональная связь
2. корреляционная связь
При функциональной связи каждому значению величины факторного признака соответствует только одно значение результативного признака. Функциональные связи обычно выражаются формулами и исследуются в математике и физике.
Пример, площадь круга – результативный признак – прямо пропорциональна его радиусу – факторный признак.
Однако, функциональные связи имеют место и в экономике.
Пример, заработная плата рабочего повременной оплате равна произведению часовой тарифной ставки на число отработанных часов.
Функциональная связь является точной и полной, т. к. обычно известны все факторы, оказывающие влияние на результативный признак. При функциональных связях величина результативного признака полностью показывается факторными признаками. Однако, в массовых явлениях общественной жизни в виду крайнего разнообразия факторов и их взаимосвязи и противоречивого действия этих факторов, не поддающихся строгому учету и контролю, возникает широкое варьирование результативного признака. Это свидетельствует о том, что связь между признаками неполная, а проявляется лишь в общем и среднем. Такие связи называются корреляционными. При корреляционной связи под влиянием изменения многих факторных признаков (ряд из которых может быть неизвестен), меняется средняя величина результативного признака.
Пример, корреляционная связь между влиянием удобрения и урожайностью культур, между производительностью и энергооснощенностью предприятия.
Важная особенность корреляционных связей состоит в том, что они обнаруживаются не в отдельных случаях, а в массовых общественных явлениях.
Проявление корреляционных зависимостей подвержено действию закона больших чисел: лишь в достаточно большом числе фактов индивидуальные особенности и второстепенные факты сгладятся и зависимость проявится достаточно отчетливо.
Вторая важная особенность корреляционных связей состоит в том, что эти связи неполные. Даже на массовых данных обнаруженные зависимости не будут носить полного, т. е. функционального характера.
В зависимости от действия функциональных и корреляционных связей их делят на:
- прямые
- обратные
Прямая связь – направление изменения результативного признака совпадает с направлением изменения признака фактора, т. е. с увеличением факторного признака увеличивается и результативный и наоборот.
Обратная связь – направление изменения результативного признака не совпадает с изменением факторного признака, т. е. при увеличении факторного признака результативный уменьшается и наоборот.
По форме связи бывают:
1. Прямолинейные – с возрастанием величины факторного признака происходит непрерывное возрастание результативного признака и наоборот.
Математически такая зависимость представляется уравнением прямой:
![]()
График представлен в виде прямой. Эту зависимость называют линейной.
2. Криволинейные – с возрастанием величины факторного признака изменение результативного признака происходит неравномерно, направление его может даже меняться. Графически этот процесс представлен гиперболой, параболой и ломаной.
Для корреляционных связей есть различия в том случае, если:
- исследуется связь между одним признаком – фактором и результативным признаком;
- исследуется связь между несколькими признаками – факторами и результативным признаком.
В первом случае имеет место парная связь и парная корреляция, во втором случае многофакторная связь и множественная корреляция.
Для исследования функциональных связей применяется индексный и балансовый метод.
3. Балансовый метод изучения взаимосвязи.
Статистический баланс представляет собой систему показателей, которая состоит их 2-х сумм абсолютных величин, связанных между собой законом равенства: 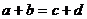
Эту сумму можно представить следующим равенством: остаток на начало + приход = расход + остаток на конец.
Товары | Остаток на 1.01 | Приход за квартал | Итого (баланс) | Продано в розницу | Продано оптом | Итого в расход | Остаток на 1.04 | Баланс |
А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
1 | 5 | 12 | 17 | 8 | 3 | 11 | 6 | 17 |
2 | 8 | 15 | 23 | 18 | - | 18 | 5 | 23 |
3 | 2 | 8 | 10 | 5 | 2 | 7 | 3 | 10 |
Итого | 50 | 50 |
Балансовый метод дает возможность не только анализировать показатели во взаимосвязи, но и осуществлять взаимный контроль данных и рассчитывать недостающие показатели.
Пример, продано в розницу = остаток на начало + приход – продано оптом – остаток на конец.
4. Измерение тесноты связи между атрибутивными признаками.
Коэффициент взаимной сопряженности Чупрова.
Для измерения тесноты связи согласованного варьирования атрибутивных варьирующих признаков применяются различные показатели, наиболее общим из них является коэффициент взаимной сопряженности Чупрова. Он применяется для сопряжения связи двух атрибутивных признаков, когда это варьирование образует 3 и более группы.
Пример, распределение 500 студентов заочников по оценкам на экзамене и характеру работы.
работы Оценки | По специальности | Не по специальности | Итого |
Отлично | 50 | 25 | 75 |
(в квадрате) | 2500 | 625 | 0,15 |
(делим на итог) | 7,1429 | 4,1666 | 11,3095 |
Хорошо | 110 | 40 | 150 |
(в квадрате) | 12100 | 1600 | 0,30 |
(делим на итог) | 34,5714 | 10,6666 | 45,238 |
Удовлетворительно | 180 | 65 | 245 |
(в квадрате) | 32400 | 4225 | 0,492 |
(делим на итог) | 92,5714 | 28,1666 | 120,738 |
Неудовлетворит. | 10 | 20 | 30 |
(в квадрате) | 100 | 400 | 0,0984 |
(делим на итог) | 0,2857 | 2,6666 | 2,9523 |
Итого | 350 | 150 | 500 |
1,0436 – эта сумма за вычетом единицы называется показателем взаимной сопряженности и обозначается ![]() , тогда коэффициент Чупрова рассчитывается:
, тогда коэффициент Чупрова рассчитывается:
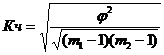 ,
,
где m – число групп по каждому признаку.
![]()
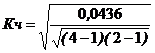 =0.1587
=0.1587
Кч изменяется от 1 до 0, но уже при значении 0,3 можно судить о тесной связи между вариацией изучаемых признаков.
Коэффициент ассоциации.
Если вариация обоих атрибутивных признаков ограничена двумя группами, то коэффициент Чупрова может быть определен проще, в виде коэффициента ассоциации. Для этого исходные данные сводятся в комбинированную четырех клеточную таблицу.
1 | 2 |
| |
1 | a | b | a + b |
2 | c | d | c + d |
| a + c | b + d |
Ка рассчитывается по формуле:
![]()
Пример, распределение населения на городское и сельское по переписям.
Место жительства | 39 г. | 70 г. | 89 г. | ||||||
г | н/г |
| г | н/г |
| г | н/г |
| |
Город | 80,9 | 19,1 | 100 | 93,8 | 6,2 | 100 | 99,8 | 0,2 | 100 |
Село | 50,6 | 49,4 | 100 | 84 | 16 | 100 | 99,5 | 0,5 | 100 |
131,5 | 68,5 | 177,8 | 22,2 | 199,3 | 0,7 |
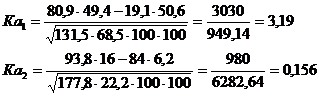

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |



