Общая дисперсия
![]()
В среднем по региону средний объем товарной продукции равен 18,14 млрд. руб.
|
|
|
|
| По АО (где а = 17) |
11 | 3 | -6 | -9 | 54 | 27 |
12 | 4 | -4 | -8 | 32 | 16 |
15 | 17 | -2 | -17 | 34 | 17 |
17 | 15 | 0 | 0 | 0 | 0 |
19 | 6 | 2 | 6 | 12 | 6 |
21 | 5 | 4 | 10 | 40 | 20 |
Итого: | 50 | 172 | 86 |
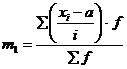 ,
, ![]()
![]()
Ср. квадратное отклонение АО: ![]()
![]() по региону средний объем товарной продукции в регионе АО 16,82
по региону средний объем товарной продукции в регионе АО 16,82
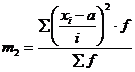 ,
, ![]()
![]()
Расчет межгрупповой дисперсии
Предприятия по форме собственности | Ср. размер ТП 1 предприятия
| Число предприятий |
|
|
|
Государственные | 20 | 50 | 1,86 | 3,4596 | 172,98 |
АО | 16,28 | 50 | -1,86 | 3,4596 | 172,98 |
![]()
![]()
![]()
![]() Закон сложения дисперсии доказан.
Закон сложения дисперсии доказан.
Если разделить дисперсию групповых средних на общую дисперсию, то получим коэффициент детерминации.
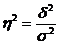
![]() - дает эмпирическое корреляционное отношение, показывает тесноту между группировочным признаком и результативным.
- дает эмпирическое корреляционное отношение, показывает тесноту между группировочным признаком и результативным.
8. Дисперсия альтернативного признака.
Среди варьирующих признаков, которые изучает статистика, встречаются признаки вариации, которые проявляются в том, что у одних единиц совокупности они встречаются, у других нет.
Признаки, которыми обладают данные единицы и не обладают другие, называются альтернативными.
Количественно вариация альтернативного признака в численности всей совокупности обозначается ![]() а доля единиц, не обладающих признаком, обозначается
а доля единиц, не обладающих признаком, обозначается ![]() и принимает значения
и принимает значения ![]() , тогда:
, тогда:
![]()
Среднее значение альтернативного признака равно доле, которая является обобщающей характеристикой совокупности по этому варьирующему признаку:
![]()
Тогда дисперсия альтернативного признака равна:
![]()
Таким образом, дисперсия альтернативного признака равна произведению доли на дополняющее эту долю до единицы число. Т. к., ![]() , то средний квадрат отклонений не может быть больше 0,25.
, то средний квадрат отклонений не может быть больше 0,25.
9. Приемы анализа вариационных рядов.
Закономерные изменения частот за счет изменения варьирующего признака в вариационных рядах называется закономерностями распределения.
Главной задачей анализа вариационных рядов является выявление закономерностей распределения и характера распределения.
Например, распределение рабочих по уровню заработной платы зависит от условий:
- квалификации;
- нормы выработки;
- расценок;
- условий труда – это общее условие.
Тип закономерности распределения – это отражение в вариационных рядах общих условий, определяющих распределение в однородной совокупности. Общие условия, определяющие тип закономерностей, познаются анализом сущности явления тех его свойств и условий, которые определяют изменчивость вариационного признака. Следовательно, должна быть построена кривая распределения. Кривая распределения – это графическое изображение частот варьирующего ряда в виде непрерывной линии, где частоты связаны с вариантами функционально. Существует теоретическая кривая распределения и фактическая.
Теоретическая кривая выражает общую закономерность данного распределения в чистом виде исключающую влияния случайных условий.
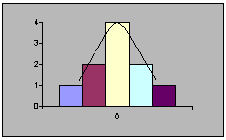 |
Рис. 4. Полигон распределения
Полигон распределения – непрерывная линия, характеризующая фактическую кривую распределения, поскольку в нем отражаются как общие, так и случайные условия, определяющие распределение.
В статистике наиболее часто для сопоставления фактических и теоретических кривых используют нормальный тип распределения, который имеет следующее уравнение:
![]()
где ![]() - ордината кривой нормального распределения /частость/,
- ордината кривой нормального распределения /частость/, 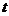 - это нормированное распределение
- это нормированное распределение ![]() .
.
В экономической статистике кривая нормального распределения (рис. 5) встречается достаточно редко, но нормальное распределение может служить моделью для выяснения степени и характера отклонения от нее фактического распределения.
 |
Рис. 5. Кривая нормального распределения
Выравнивание фактического распределения по кривой нормального распределения.
Cостоит из нескольких этапов:
- сравнивают фактические и теоретические частоты. По фактическим данным определяют теоретические частоты кривой нормального распределения, которая является функцией нормированного отклонения;
- проверяют на сколько распределение признака соответствует нормальному.
|
|
|
|
| Теоретическая частота | Комулятивная частота |
| |
фактич. | теоретич. | |||||||
195 | 2 | 45,2 | 2,469 | 0,01888 | 1,2895 | 2 | 1,3 | 0,7 |
205 | 5 | 35,2 | 1,240 | 0,06316 | 4,3138 | 7 | 5,6 | 1,4 |
215 | 13 | 25,2 | 1,377 | 0,15395 | 10,5247 | 20 | 16,1 | 3,6 |
225 | 17 | 15,2 | 0,830 | 0,28269 | 19,3077 | 37 | 35,4 | 1,6 |
235 | 18 | 5,2 | 0,284 | 0,38361 | 26,2005 | 55 | 61,6 | -6,6 |
245 | 31 | 4,8 | 0,262 | 0,38568 | 26,3419 | 86 | 87,9 | -1,9 |
255 | 22 | 14,8 | 0,808 | 0,28737 | 19,627 | 108 | 107,5 | 0,5 |
265 | 12 | 24,8 | 1,355 | 0,15822 | 10,806 | 120 | 118,3 | 1,7 |
275 | 5 | 34,8 | 1,901 | 0,06562 | 4,4818 | 125 | 122,8 | 2,2 |
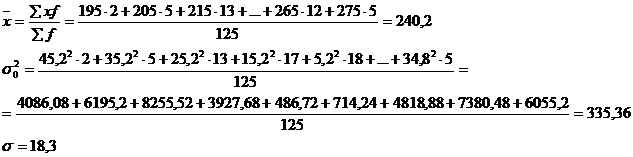

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |



