«Статистика» (стр. 6 )

Коэффициент вариации применяется в следующих случаях:

-  когда необходимо определить и сравнить степени рассеивания 2-х или нескольких признаков, выраженных в различных единицах измерения для характеристики одной и той же совокупности;

-  когда необходимо определить рассеивание одного и того же признака в разных единицах совокупности, имеющих разные единицы измерений и разные ср. величины.

Если коэффициент вариации составляет более 0,40 то такая совокупность считается неоднородной.

Пример.

Имеются данные о стаже работы рабочих 3-х бригад:

I бригада – 15, 18, 20, 22, 25 лет;

II бригада – 10, 15, 20, 25, 30 лет;

III бригада – 8, 12, 17, 25, 38 лет.

Определить показатель вариации.

1. Размах вариации.

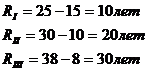
2. Среднее линейное отклонение.

I.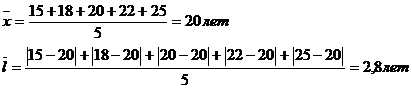

II.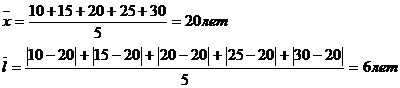

III.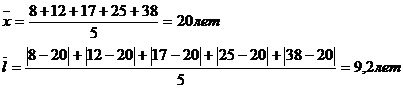

В I бригаде абсолютное отклонение каждого значения от средней величины 2,8 лет, во II бригаде – 6 лет, в III бригаде – 9,2 лет.

3. Дисперсия, средний квадрат отклонения.

I.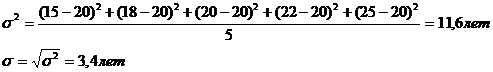

II.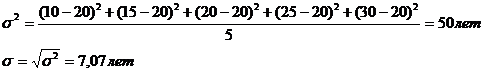

III.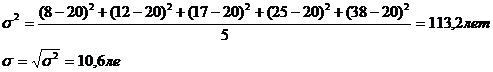

Чем больше ср. квадратическое отклонение, тем более высока вариация, т. е. более неточным будет среднее значение.

4. Коэффициент вариации.

I.

II.

III.

III бригада является неоднородной совокупностью, т. к. коэффициент вариации составляет более 0,40.

5. Показатели относительного рассеивания.

Данные показатели позволяют охарактеризовать совокупность, а в частности колеблимость изучаемого признака. Показатели относительного рассеивания определяются путем деления меры относительного рассеивания на среднюю арифметическую величину и выражаются в %. К таким показателям относятся:

1). Коэффициент осцеляции – определяется как отношение размаха вариации к средней величине признака и характеризует относительную рассеянность или колеблимость крайних значений признака вокруг средней:

,

где – размах вариации. Этот показатель показывает на сколько % отклоняется среднее от крайних значений вариации.

Если >100, то (крайних значений признака) и наоборот.

2). Относительное линейное отклонение.-средние линейное отклонение делим на среднюю величину, ия:

Пример.

Рассчитать показатели вариации и показатели относительного рассеивания по данным таблицы.

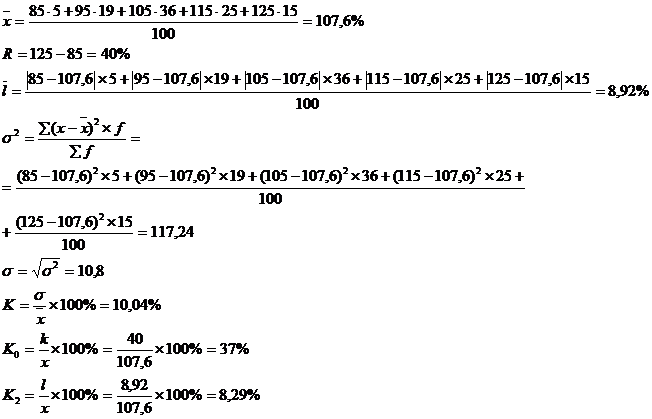
6. Закон сложения дисперсии.

Если статистическая совокупность разбита на несколько групп по одинаковому признаку, то средняя величина и дисперсия могут быть определены не только для всей совокупности, но и для отдельной ее части. В зависимости от этого можно выделить межгрупповую и внутригрупповую вариацию. А, следовательно, рассчитать среднюю величину и дисперсию, как межгрупповую, так и внутригрупповую.

В зависимости от всех условий в совокупности определяют общую дисперсию, которая зависит от этих условий:

где - общее среднее для всей изучаемой совокупности, т. е. среднее для всех групп, входящих в совокупность.

Межгрупповая дисперсия отражает вариацию признака изучаемой совокупности, изменение признака которой возникает под влиянием фактора, положенного в основу группировки.

Межгрупповая дисперсия характеризует колеблимость групповых средних около общей средней:

где - средняя величина признака по относительным группам;

- частота отдельных групп.

Средняя внутригрупповая дисперсия характеризует случайную вариацию в каждой отдельной группе. Данная вариация возникает в зависимости от влияния других факторов, которые не учитываются при группировке.

Между общей дисперсией и средней из групповой дисперсии и межгрупповой существует взаимосвязь:

– закон сложения дисперсии

7. Свойства дисперсии.

1.  Если из всех значений вариант вычесть какое-то постоянное число, то средний квадрат отклонений не изменится:

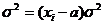
2.  Если все значения вариант разделить на какое-то постоянное число, то средний квадрат отклонений уменьшиться в а раз:

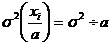
3.  Если средний квадрат отклонений от любой величины а – которая отличается от средней арифметической х, то он будет всегда больше среднего квадрата отклонений от средней арифметической: 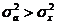, но больше на определенную величину, а эта величина определена, как квадрат разности между средней и этой, условно взятой величиной:

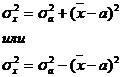
используя 2-ое свойство дисперсии в математической статистике можно рассчитать дисперсию способом моментов. Средний квадрат отклонений от средней величины имеет свойства min, т. е. дисперсия от средней всегда меньше дисперсий исчисляемых от других величин. В этом случае, если а – постоянное число = 0, то, следовательно, средний квадрат отклонений будет определяться по формуле:

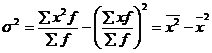
- ср. квадрат значений признака;

- квадрат среднего значения признака.

Значит, средний квадрат отклонений равен разности между средним квадратом значения признака и квадратом ср. значения признака.

Также способ моментов называется способом отсчета от условного нуля. Данный способ можно применять только в тех случаях, если в вариационных интервальных рядах интервалы одинаковы.

Используя 2-ое свойство дисперсии, разделив все варианты на величину интервала, получим формулу дисперсии:

где i – величина интервала для данной совокупности ;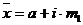

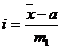
Пример.

Рассчитать все показатели вариации, доказать закон сложения дисперсии.

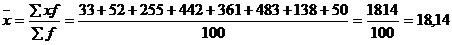
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22