Решение. Сделаем рисунок, соответствующий условию задачи – рис.13.
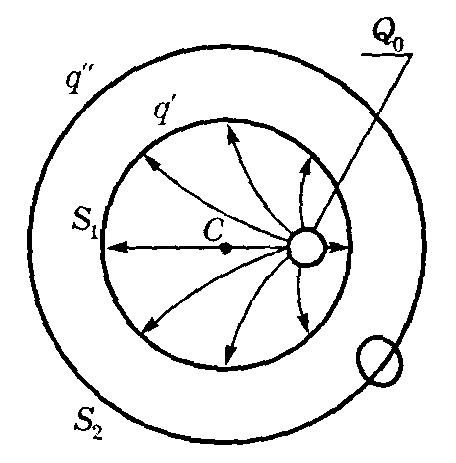
Рис.13
В случаях, когда металлический шар не касается оболочки, на внутренней и внешней поверхностях оболочки появляются индуцированные заряды. Эти заряды обеспечивают равенство нулю напряженности электрического поля в толще металлической оболочки. Если заряд шара положительный, то на внутренней поверхности оболочки индуцируется отрицательный заряд. Используя теорему Остроградского – Гаусса можно показать, что индуцированный заряд на внутренней поверхности оболочки равен:
(1)
Аналогично на внешней поверхности оболочки индуцируется положительный заряд, равный заряду шара:
(2)
Теперь рассмотрим особенности каждого случая, предложенного в задаче.
1. Шар расположен в центре оболочки концентрично. При этом заряды распределяются по соответствующим поверхностям равномерно. Потенциал электрического поля в центре оболочки можно найти по принципу суперпозиции как сумму потенциалов, созданных в этой точке зарядом, находящимся на внешней поверхности, зарядом, находящимся на внутренней поверхности оболочки, и зарядом шара. Из теоремы Остроградского – Гаусса эти потенциалы определены:
, 
, 
.
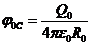Используя соотношение (2), получаем6
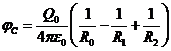
Подставляем численные значения в последнюю формулу и вычисляем потенциал электрического поля в центре оболочки: 
.
В точке, лежащей на внешней поверхности оболочки, потенциал находится по тому же принципу:
.
Из теоремы Остроградского – Гаусса эти потенциалы известны:
.
Подставляем эти выражения в предыдущую формулу и, и учитывая соотношение между зарядами (2), получаем:
.
Подставляем в эту формулу численные значения и вычисляем потенциал электрического поля в точках на внешней поверхности оболочки: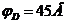 
.
2. Центр шара смещен на расстояние 
от центра оболочки. В этом случае потенциал электрического поля, созданного зарядом на внешней поверхности оболочки, в центре оболочки определяется такой же формулой, как и в предыдущем случае: .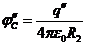
Потенциал, создаваемый зарядом внутренней поверхности оболочки, распределение которого по этой поверхности теперь неизвестно, можно найти по принципу суперпозиции. Для этого разобьем заряд на элементарные заряды, которые можно считать точечными, а затем проведем интегрирование:
. Теперь учтем, что расстояние от любого элементарного заряда 
, расположенного на внутренней поверхности оболочки, до центра оболочки одинаково. Тогда последний интеграл можно записать в виде: 
.
Потенциал, создаваемый зарядом шара, также будем искать по принципу суперпозиции:
, где 
- переменное расстояние от элемента заряда шара 
до точки 
. Распределение заряда 
по поверхности шара неизвестно, поэтому значение потенциала 
определить нельзя. Однако этот потенциал можно оценить. Расстояния от различных элементов заряда шара до центра шара изменяется от 
до 
. Если в выражении для потенциала электрического поля шара переменную заменить значением 
, то потенциал можно определить неравенством:
.
Если в эту формулу подставить численные значения, то получим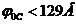 
.
Если в выражении для потенциала переменную заменить значением 
, то этот потенциал можно определить неравенством:
.
Вычисления по последней формуле показывают, что 
.
Из полученных значений следует, что 
или 
. Что дает относительную погрешность около 7%.
Таким образом, с учетом соотношения между зарядами (2), можно записать
.
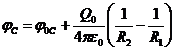Подставив численные значения в последнюю формулу, получим
.
В точках на внешней поверхности оболочки поле создается только зарядом, расположенным на этой оболочке. Тогда, как и в первом случае, получаем: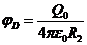 
. Численное значение этого потенциала равно 
.
3. Шар соприкасается с оболочкой. В этом случае заряд шара передается оболочке, а так как оболочка металлическая, то он будет распределен по ее внешней поверхности. Поэтому потенциал определяется только зарядом, распределенным на внешней поверхности оболочки. Тогда 
. Численное значение этого выражения было определено: 
.
Ответ: 1. 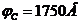; ; 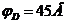2. ; ;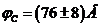
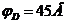3. .
Задача 11. Точечный заряд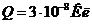 
находится на расстоянии 
от большой тонкой металлической пластины, соединенной с Землей. Определить: 1) потенциал в точках 
и , симметрично расположенных по обе стороны пластины на расстоянии 
от нее, причем точка , ближайшая к заряду 
, находится от него на расстоянии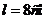 
; 2) поверхностную плотность зарядов, индуцированных на пластине в точке 
, находящейся на расстоянии 
от заряда ; 3) заряд индуцированный на пластине.
Решение. Сделаем рисунок, соответствующий условию задачи. – рис. 14. при внесении металлической пластины в поле точечного заряда на ней появляются индуцированные заряды. При этом на поверхности, обращенной к заряду, создающему поле, индуцируется заряд, знак которого противоположен знаку заряда, создающего поле. Поэтому в решаемой задаче на стороне пластины, обращенной к заряду , будет индуцироваться отрицательный заряд. Положительных зарядов на противоположной стороне пластины в решаемой задаче нет, так как пластина заземлена.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
