Методические рекомендации к практическим занятиям по курсу общей физики для студентов для направления подготовки 650800 «Теплоэнергетика» и специальности 100700– «Промышленная теплоэнергетика» (стр. 8 )

Решение. Сделаем рисунок, соответствующий условию задачи.

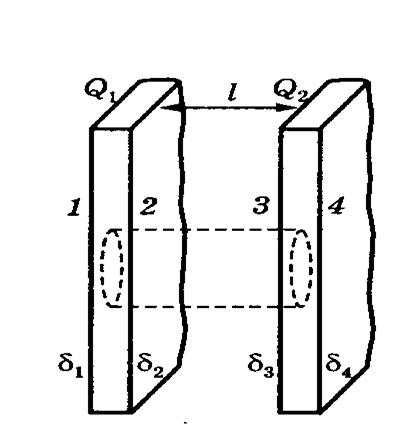
Рис.12

По условию задачи размеры пластин велики. В этом случае можно пренебречь зарядами на торцевых поверхностях и считать, что на каждой из четырех боковых поверхностей 1, 2 ,3, 4 заряды распределены равномерно. Тогда напряженность результирующего поля определяется выражением:

(1)

Здесь

, (2)

где - результирующая поверхностная плотность сообщенных и индуцированных зарядов на боковой поверхности пластины. При этом формула (2) может быть получена из теоремы Остроградского – Гаусса. Из условий задачи следует, что электрическое поле между пластинами однородно и тогда разность потенциалов между пластинами можно найти по формуле:

(3)

Таким образом, чтобы найти напряженность электрического поля, надо определить поверхностные плотности зарядов на всех четырех боковых поверхностях. Это можно сделать на основе закона сохранения заряда. Если и = поверхностные плотности зарядов на поверхностях первой пластины, то по закону сохранения заряда имеем:

(4)

Если и - поверхностные плотности зарядов на поверхностях второй пластины, то

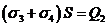(5)

Распределение зарядов на поверхностях пластин должно быть таким, чтобы напряженность электрического поля в толще металла была равна нулю. Используем это условие, для чего выберем цилиндрическую поверхность. Основания этой поверхности находятся внутри металлических пластин, а боковая поверхность соединяет пластины. Теперь используем теорему Остроградского – Гаусса. Поток вектора напряженности через боковую поверхность выбранного цилиндра равен нулю, так как силовые линии электрического поля перпендикулярны пластинам, и поэтому во всех точках боковой поверхности скалярное произведение 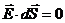. Поток через основания цилиндра обращается в нуль, так как оба основания находятся в толще металла, где напряженность электрического поля равна нулю. Следовательно, поток через полную замкнутую поверхность выбранного цилиндра равен нулю: 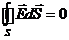. Теперь определим суммарный заряд, находящийся внутри этой поверхности: 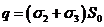, где - площадь основания выбранной цилиндрической поверхности. По теореме Остроградского – Гаусса имеем . Отсюда следует, что

(6)

Из этого равенства следует, что электрические поля, создаваемые поверхностями 2 и 3, внутри каждой из рассматриваемых пластин взаимно скомпенсированы. Векторы и в этих областях направлены в противоположные стороны и равны по модулю. Так как в толще пластин напряженность электрического поля равна нулю, то поля, создаваемые зарядами на поверхностях 1 и 4, также должны быть скомпенсированы. Так как напряженности электрического поля, созданного зарядами на поверхностях 1 и 4, в толще пластин должны быть противоположно направлены, то

(7)

Уравнения (4), (5), (6) и (7) образуют систему, решение которой позволит найти распределение зарядов, а затем и разность потенциалов между пластинами.

В пространстве между пластинами векторы и направлены в противоположные стороны и с учетом формулы (7) можно записать:

.

Векторы и , как следует из формулы (6) направлены в пространстве между пластинами в одну сторону. Тогда из формулы (1) следует:

.

Теперь по формуле (3) можно найти разность потенциалов между пластинами:

(8)

Из формулы (8) видно, что знак разности потенциалов зависит от .

Теперь рассмотрим различные предложенные в задаче ситуации.

1. . Из формулы (5) получаем . Таким образом для данного случая имеем систему уравнений:

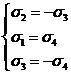
Решая эту систему, получаем . Теперь можно воспользоваться определением поверхностной плотности заряда:

Подставляем численные значения и определяем поверхностную плотность заряда на каждой поверхности:

.

Теперь вычислим по формуле (8) напряжение между пластинами: .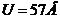

2.. Теперь система уравнений из формул (4), (5), (6) и (7) имеет вид:

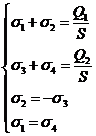
Решим эту систему и получим:

.

Теперь подставим численные значения зарядов и получим:

Используя формулу (8) вычислим разность потенциалов между пластинами в этом случае .

3. и вторая пластина заземлена. При соединении внешней поверхности правой пластины с Землей, потенциал которой принимается за ноль, потенциал этой пластины также становится равным нулю. Это значит, что в области справа от заземленной поверхности напряженность поля равна нулю. В толще второй пластины напряженность тоже равна нулю, так как пластина металлическая. Это значит, что на поверхности 4 вектор напряженности электрического поля не имеет разрыва. Это может быть в случае, когда зарядов на этой пластине нет. Тогда можно сразу записать, что . Теперь из формулы (7) следует, что . Тогда из формулы (4) найдем:. Формула (6) позволяет определить .

Подставляем численные значения и получаем:

.

По формуле (8) вычислим разность потенциалов между пластинами в данном случае .

В данной задаче размерность полученных величин легко проверялась устно на основе определения этих величин.

Ответ: 1. , ;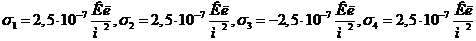

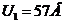2. , ;

3. , .

Задача 10 Внутри сферической металлической оболочки радиусами и находится металлический шар радиуса с зарядом . Найти потенциалы в точке, являющейся центром оболочки, и на внешней поверхности оболочки, если 1) шар расположен концентрично оболочке; 2) центр шара смещен на расстояние от центра оболочки; 3) шар соприкасается с оболочкой.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13