В точке 
вектор напряженности электрического поля направлен вертикально вверх параллельно оси 
, по модулю 
.
Найдем потенциал и напряженность электрического поля в точке 
:
; 
; 
.
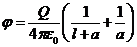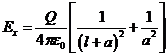Теперь устно легко проверить размерность полученных величин, для чего используем формулу для потенциала и напряженности поля точечного заряда. После проверки размерности можно подставить численные значения и получить результаты:
; 
; .
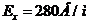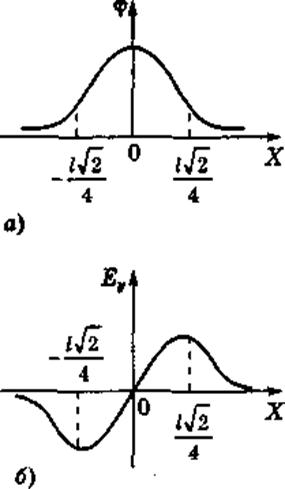
Теперь проанализируем выражения для потенциала и напряженности электрического поля при различных возможных положениях исследуемой точки поля:
а) При расчете 
по формуле (2) в точках, где 
а 
выражение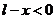 
а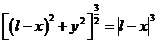 
. В точке вектор напряженности направлен вдоль оси 
и при этом 
.
Для точек, лежащих на прямой, соединяющей заряды и тогда, согласно формуле (1) выражение для потенциала будет иметь вид:
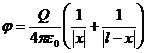
Для этих точек 
при любом значении 
. Из последней формулы видно, что 
при 
и при 
. Из последней формулы видно, что в области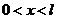 
потенциал имеет минимум. Из выражения для (по формуле (2)) для точек видно, что потенциал имеет минимум при 
. Тогда примерный график 
для этой прямой () имеет вид, показанный на рисунке 3 а.
Теперь построим график зависимости напряженности электрического поля от координаты для точек, лежащей на той же прямой, на которой лежат заряды, то есть . При этом из формулы (2) следует, что
, .
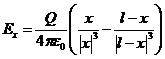Теперь из этого выражения следует:
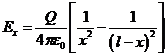, где .
Из последней формулы следует, что 
, если 
и 
, если 
.
Теперь легко получить выражения для напряженности электрического поля вне указанной области (с учетом знака зарядов):
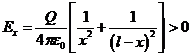, если и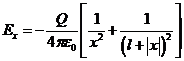 
, если 
.
Из этих формул следует, что напряженность терпит разрыв в точках 
и 
. При этом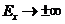 
, если , и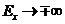 
, если . График зависимости 
представлен на рисунке 3 б.
Теперь рассмотрим точки, лежащие на прямой
, для которых . В этом случае выражения (1) и (2) принимают вид:
; 
; 
.
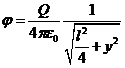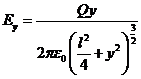Из этих формул следует, что при всех значениях координаты 
. Знак проекции 
определяется знаком координаты .
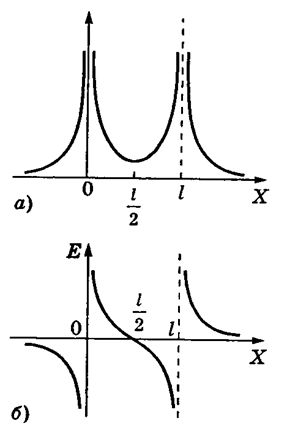
Рис.3
При 
производная 
, и следовательно, принимает экстремальные значения. Соответственно, для функции 
это будут точки перегиба. Примерные графики и 
показаны на рисунке 4 а и 4 б.
Ответ: В точке С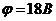 
, , 
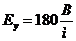. В точке В , , .
|
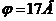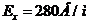Рис.4
Задача 4. Тонкий стержень длиной 10 см равномерно заряжен зарядом 
Кл. Найти напряженность и потенциал электрического поля в точке С, лежащей на оси стержня на его продолжении. Расстояние от середины стержня до этой точки равно 20 см. Определить, при каких условиях напряженность можно рассчитывать по формуле напряженности электрического поля точечного заряда, если относительная погрешность не превышает 5%.
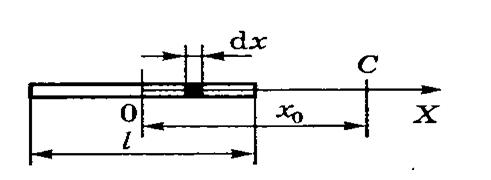
Рис.5
Решение. Ситуация, описанная в задаче, схематично изображена на рисунке 5. Здесь электрическое поле создается зарядом, распределенным по стержню. В этом случае очень трудно установить точное расположение силовых линий, поэтому для определения характеристик электростатического поля будем использовать принцип суперпозиции. Для этого разобьем стержень на элементарные участки длины 
, которые имеют заряд 
. Каждый такой участок стержня можно считать точечным зарядом. Как известно точечный заряд создает электрическое поле, потенциал которого можно определить по формуле:
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
