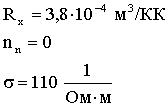где с - скорость света. Тогда:
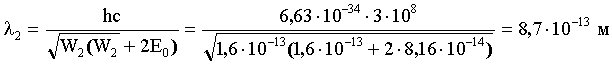
Ответ:
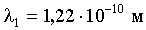 ;
;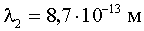
Задача 2. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l на втором энергетическом уровне. В каких точках ямы плотность вероятности обнаружения частицы совпадает с классической плотностью вероятности?
Дано: |
|
Найти: | x. |
Решение: Волновая функция ψ, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме шириной l, имеет вид:
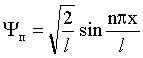 (1)
(1)
где n - номер энергетического уровня (n = 1,2,3...), х - координата частицы в яме (0 ≤ х ≤ l).
Согласно физическому смыслу волновой функции:
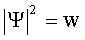 (2)
(2)
где w - плотность вероятности обнаружения частицы в точке с координатой х.
Если частица находится на втором энергетическом уровне (n = 2), т. е.:
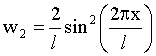 (3)
(3)
Выражение для классической плотности вероятности имеет вид:
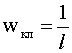 (4)
(4)
Приравнивая по условию выражения (3) к (4), получим:
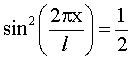 (5)
(5)
Решая уравнение (5), найдем:
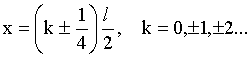
В пределах ямы (0 ≤ х ≤ l) таких точек четыре:
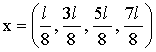
Ответ:
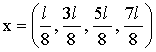
Задача 3. Некоторый примесный полупроводник имеет решетку типа алмаза и обладает только дырочной проводимостью. Определить концентрацию дырок nр и их подвижность uр, если постоянная Холла Rх = 3,8·10-4 м3/Кл. Удельная проводимость полупроводника σ =110 (Ом·м)-1.
Дано: |
|
Найти: | nр, uр. |
Решение: Концентрация дырок nр связана с постоянной Холла, которая для полупроводников с решеткой типа алмаза, обладающих носителями только одного знака, выражается формулой:
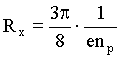 (1)
(1)
где е - элементарный заряд.
Отсюда:
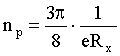 (2)
(2)
Подставим числовые значения величин в формулу (2) и проведем вычисления:
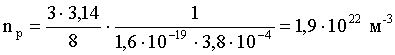
Удельная проводимость полупроводников выражается формулой:
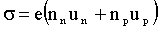 (3)
(3)
где nn и np - концентрации электронов и дырок, un и up - их подвижности.
При отсутствии электронной проводимости первое слагаемое в скобках равно нулю, и формула (3) примет вид:
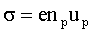
Отсюда искомая подвижность:
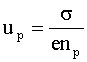 (4)
(4)
Подставим в (4) выражение nр, описываемое формулой (2):
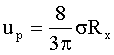 (5)
(5)
Подставим в (5) численные значения и проведем вычисления:
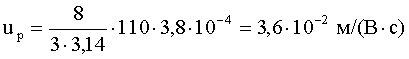
Внимание
Данное пособие будет постоянно пополняться новыми образцами решения задач. Для подготовки к практическим занятиям и к выполнению контрольных работ студенты могут воспользоваться многочисленными пособиями, в которых приводятся образцы решения задач. Эти пособия указаны в рабочей программе. Здесь же укажем наиболее распространенное пособие – , Павлова задач по курсу физики с решениями. – М.: Высшая школа, 1999. – 591 с. Это пособие есть в электронном виде на кафедре общей и экспериментальной физики. Оно также размещено в Интернете в электронной библиотеке DjVu. Для того чтобы найти электронную версию этого пособия достаточно на Яндексе набрать фамилию автора, название пособия и DjVu.
Список рекомендуемой литературы
Основная литература
1 , Яворский физики. – М.: Высшая школа, 1989.
2 Савельев общей физики: В 3 т. – М.,: Наука,1978-1990.
3 Трофимова физики. – М.: Высшая школа, 1990.
4 Волькенштейн задач по общему курсу физики. – М.: Наука, 1979 – 1990.
5 , Павлова задач по курсу физики с решениями. – М.: Высшая школа, 1999. – 591с.
Дополнительная литература
6 Стрелков . – М.: Наука, 1975.
7 Кикоин физика. – М.: Наука, 1976.
8 Калашников . – М.: Наука, 1977.
9 Ландсберг . – М.: Наука, 1976.
10 Епифанов твердого тела. – М.: Высшая школа. 1977.
11 Иродов по общей физике. – М.: Наука, 1979.
12 , , Федоров по физике. – М.: Высшая школа, 1973, 1981.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 |