,
где 
расстояние от точечного элемента 
до изучаемой точки С. Потенциал результирующего поля определяется интегрированием последней формулы по всему заряду, распределенному по стержню:
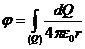(1)
Так как нужно найти напряженность и потенциал поля в точках, лежащих на продолжении стержня, введем ось OX, направленную по стержню. Тогда положение элемента определяется его координатой на выбранной оси, а расстояние от этого элемента до точки С равно
(2)
Симметричность условий распределения заряда позволяет сделать вывод, что в точках, лежащих на оси OX, вектор напряженности электростатического поля направлен вдоль этой оси. Тогда на основе связи напряженности и потенциала имеем:
; 
. (3).
Равномерное распределение заряда по стержню позволяет записать следующее условие для 
: 
, откуда следует, что 
. При интегрировании по заряду стержня нужно учесть что 
изменяется в пределах от 
до 
. Тогда из формул (1) и (2) следует что потенциал определяется интегралом: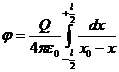 
. Этот интеграл легко вычисляется, и в результате получаем: 
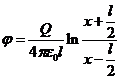(4).
Размерность этой величины легко проверяется устно по известной формуле потенциала поля точечного заряда. Теперь можно подставить численные значения и вычислить потенциал поля в точке С:
, 
.
Напряженность электрического поля найдем по формуле (3), используя выражение для потенциала поля формулу (4):
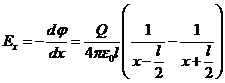(5)
Здесь мы нашли проекцию вектора напряженности на ось OX. Так как 
, то 
и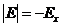 
, если 
(справа от стержня). Аналогично имеем 
, если 
, и 
, если (слева от стержня). При этом необходимо помнить, что полученные формулы для потенциала и напряженности электрического поля справедливы только в случае, если 
.
Размерность величины, определяемой формулой (5), легко проверяется устно. Подставляя в формулу (5) значение 
, вычисляем напряженность электрического поля в точке С: 
, причем вектор напряженности электрического поля направлен противоположно направлению оси OX.
Чтобы ответить на вопрос, при каком условии в данной ситуации можно использовать формулы напряженности и потенциала поля точечного заряда, проанализируем формулу (5). Преобразуем выражение в скобках формулы (5), для чего приведем это выражение к общему знаменателю и вынесем множитель 
в знаменателе:
.
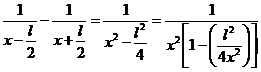В случае, если 
выражение 
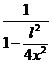можно разложить в ряд Тейлора. При этом получим:
.
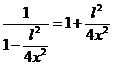После этих преобразований выражение для напряженности электрического поля будет иметь вид:
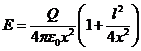(6)
Если , то этой величиной можно пренебречь по сравнению с единицей. Тогда напряженность электрического поля можно определить по формуле, совпадающей с формулой напряженности электрического поля точечного заряда. Это значение будет приближенным, то есть
(7)
Сравним выражения для напряженности, полученные по формулам (6) и (7) и определим погрешность приближенного расчета:
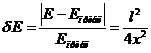
По условия задачи
. Теперь можно подсчитать значение 
для указанной погрешности. При расчете получим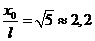 
. Это говорит о том, что даже при таком небольшом удалении от стержня можно использовать формулу для напряженности и потенциала точечного заряда, если допустимая погрешность составляет 5%.
Ответ: ,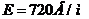 
,
.
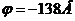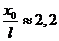Задача 5. Положительный заряд 
равномерно распределен по тонкому проволочному кольцу радиуса 
. Определить напряженность и потенциал электрического поля в точке С, лежащей на оси кольца на расстоянии 
от его центра.
Решение. Сделаем рисунок, соответствующий условию задачи – рис.6. Поле создано зарядом, распределенным по тонкому кольцу заданного радиуса. Указать точно геометрию силовых линий создаваемого таким зарядом поля трудно. Поэтому для определения напряженности и потенциала поля используем принцип суперпозиции. Разобьем кольцо на элементарные точечные участки, которые имеют заряд . Потенциал электрического поля, созданного таким зарядом, определяется формулой для потенциала электрического поля, созданного точечным зарядом:
, (1)
где - расстояние от элемента до точки С.
Потенциал результирующего поля получим интегрированием выражения (1) по всему заряду:
(2).
Если ввести систему координат, то проекции вектора напряженности на координатные оси можно определить дифференцированием полученного выражения для потенциала по соответствующей координате.
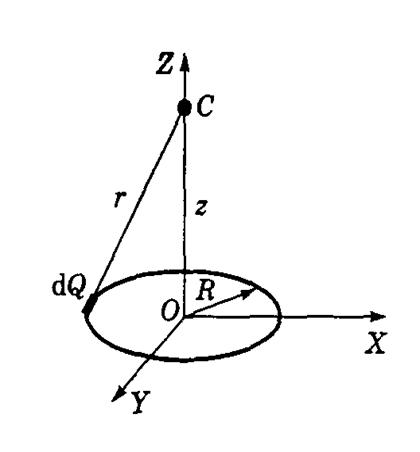
Рис.6
В данной задаче при переходе от одного элемента кольца к другому величина 
не изменяется. Поэтому интеграл в формуле (2) можно представить в виде:
.
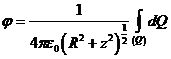Очевидно, что независимо от закона распределения заряда по кольцу 
. Тогда потенциал электрического поля в точках на оси кольца равен: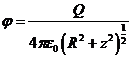 
(3).
Тогда проекция вектора напряженности на ось 
определяется выражением:
(4)
При равномерном распределении заряда по кольцу из симметрии задачи следует, что вектор напряженности 
направлен вдоль оси . Тогда 
. При 
, если заряд положительный, 
и вектор направлен по оси , то есть вверх. В области 
и вектор напряженности направлен против оси , то есть вниз.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
