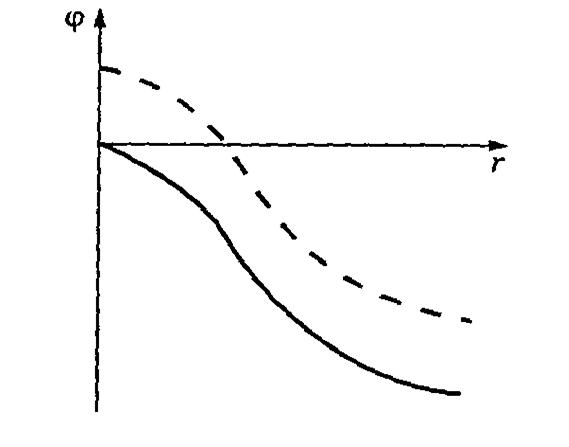
Рис.9
Ответ: При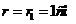 
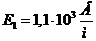, а при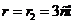 
, 
.
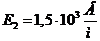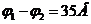Задача 7. В одной плоскости с очень длинной нитью, равномерно заряженной с линейной плотностью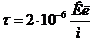 
, под углом 
300 к нити расположен тонкий стержень длиной 12см, по которому равномерно распределен заряд 
. Расстояние от нити до середины стержня равно 8 см. найти силу, действующую на стержень, и ее предельные значения при 
и 
.
Решение. Сделаем рисунок, соответствующий условиям задачи – рис.10. Здесь электрическое поле создается заряженной нитью. Силовые линии такого поля расположены радиально от нити, а проекция вектора напряженности на радиальное направление определяется формулой, полученной из теоремы Остроградского – Гаусса:
.
Из последней формулы видно, что напряженность электрического поля нити зависит от расстояния до изучаемой точки. Так как стержень расположен под углом к нити, то для определения силы необходимо сначала записать выражение для силы, действующей на элементарный участок стержня длиной 
с зарядом 
:
.
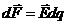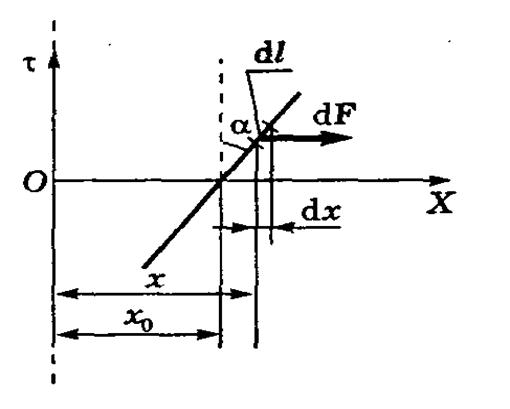
Рис.10
Стержень находится в одной плоскости с нитью, и эта плоскость совпадает с плоскостью рисунка. В этой плоскости силовые линии электрического поля, созданного заряженной нитью, параллельны друг другу. В этом случае все элементарные силы 
, действующие на различные элементарные участки стержня, направлены одинаково, поэтому результирующая сила определяется формулой:
(1)
Эта сила направлена так же, как и силовые линии электрического поля нити. Для расчетов введена ось 
. Тогда элемент длины стержня можно найти по формуле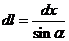 
. Заряд этого элемента длины стержня найдем по формуле 
.
Расстояние от нити до рассматриваемого элемента стержня 
, тогда сила, действующая на этот элемент стержня, определяется формулой:
(2)
При интегрировании последней формулы по всей длине стержня надо учесть, что координата 
изменяется от 
до 
.
Подставляем (2) в (1) с учетом указанных пределов изменения переменной , получаем:
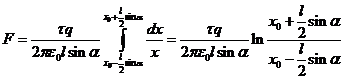. (3)
Проверим размерность полученной величины:
.
Теперь можно подставить численные значения и вычислить искомую величину.
При 
.
При 
.
При стержень расположен параллельно нити. Напряженность электрического поля вдоль всего стержня одинакова: 
. Тогда сила, действующая на стержень в этом случае, определяется по формуле:
. Теперь подставим численные значения и вычислим величину силы: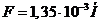 
.
Последнюю формулу можно получить из формулы (3), если разложить натуральный логарифм в ряд с последующим предельным переходом 
.
Ответ: При 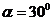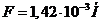, а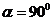 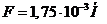при . При .
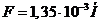Задача 8. Точечный заряд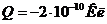 
расположен на продолжении оси диполя, электрический момент которого 
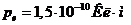, на расстоянии 
от его центра ближе к положительному заряду диполя. Какую работу надо совершить, чтобы перенести этот заряд в симметрично расположенную точку по другую сторону диполя? Плечо диполя 
.
Решение. Сделаем рисунок, соответствующий условию задачи – рис. 11. Работа, совершаемая внешними силами при перемещении заряда в кулоновском поле, равна работе сил поля, взятой с обратным знаком:
, (1)
где 
и 
- потенциалы начальной и конечной точки соответственно. Электрическое поле создается диполем, то есть двумя зарядами 
и 
. Потенциалы точек 1 и 2 будем искать, используя принцип суперпозиции. Как видно из рисунка и условия задачи, точка 1 находится на расстоянии 
от
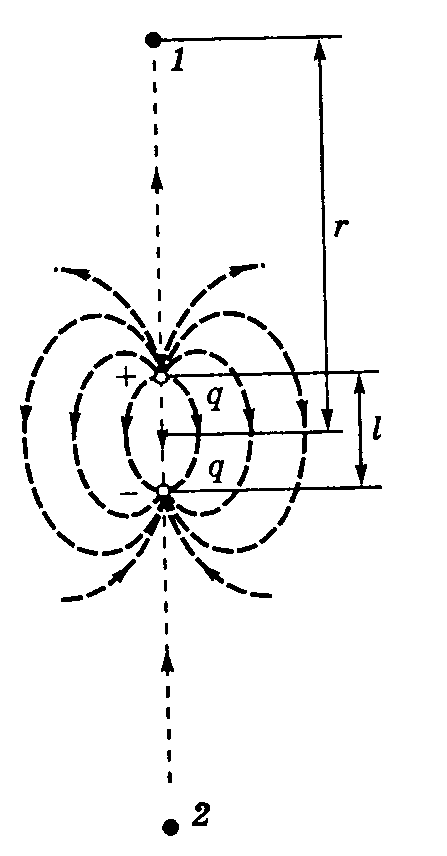
Рис.11
положительного заряда и на расстоянии 
от отрицательного заряда. Тогда по принципу суперпозиции можем найти потенциал точки 16
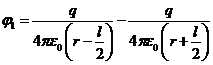(2)
Аналогично найдем потенциал точки 2:
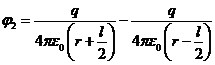(3)
Приведем формулы (2) и (3) к общему знаменателю:
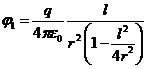(4)
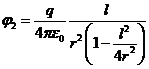. (5)
Учтем, что 
, и при 
величинами 
можно пренебречь по сравнению с единицей. Тогда формулы (4) и (5) будут иметь вид:
, 
.
Подставляя эти выражения в формулу (1), получим
.
Проверим размерность полученной величины:
.
Теперь можно подставить численные значения и вычислить работу:
.
Ответ: .
Задача 9. Две металлические пластины, заряды на которых 
и 
, расположены параллельно друг другу на расстоянии 
. Площадь каждой пластины 
. Считая, что линейные размеры пластин несоизмеримо велики по сравнению с расстоянием между ними 
и толщиной пластин, найти поверхностные плотности зарядов и разность потенциалов между пластинами. Задачу решить для случаев 1) 
; 2) 
; 3) , но пластина заземлена.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
