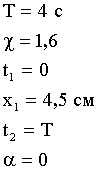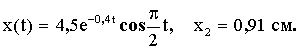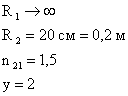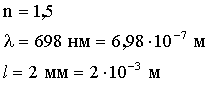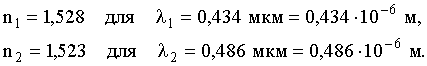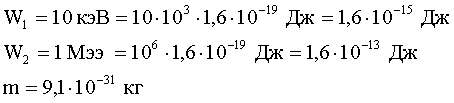Дано: |
|
Найти: |
|
Решение: Уравнение затухающих колебаний имеет вид:
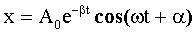 (1)
(1)
где β - коэффициент затухания, ω - частота затухающих колебаний.
Найдем ω:
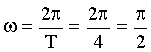
Логарифмический декремент затухания связан с коэффициентом затухания: ![]() . Отсюда:
. Отсюда:
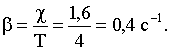
Подставим ω, β, α в (1) и найдем смещение:
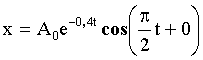
Для начального момента времени при t = 0:
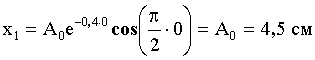
Уравнение колебаний имеет вид:
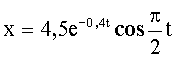
Смещение в момент ![]() :
:
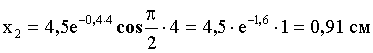
Ответ: |
|
6 Примеры решения задач по оптике
Задача 1. На каком расстоянии от предмета нужно поместить экран, чтобы плоско выпуклая линза с радиусом кривизны R = 20 см и показателем преломления n = 1,5 давала изображение предмета, увеличенное в 2 раза?
Дано: |
|
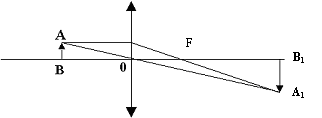
Рис.6 |
Найти: | a |
Решение: Построим изображение предмета (рис. 6). Из чертежа следует, что ΔАОВ ˜ΔА1 ОВ1 . Из подобия следует:
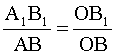
По условию задачи увеличение 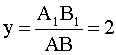 . Следовательно:
. Следовательно:
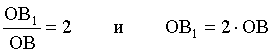 (1)
(1)
Из принятых обозначений: ОВ = d, ОВ1 = f. Тогда: f = 2d. Определим оптическую силу линзы:
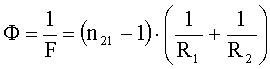 (2)
(2)
Проведем вычисления:
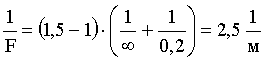
Воспользуемся формулой тонкой линзы:
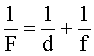 (3)
(3)
Подставим (1) в (3):
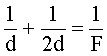
Тогда
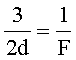
Найдем расстояние от предмета до линзы
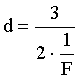
Вычислим:
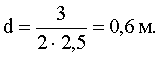
Расстояние от предмета до экрана равно:
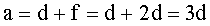
![]()
Ответ: а = 180 см.
Задача 2. На стеклянный клин падает нормально монохроматический свет (λ = 698 нм). Определить угол между поверхностями клина, если расстояние между соседними интерференционными минимумами в отраженном свете равно 2 мм.
Дано: |
|
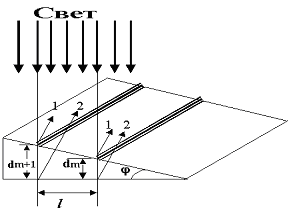
Рис.7 |
Найти: | φ |
Решение: Параллельный пучок света, падая нормально к грани, отражается как от верхней (луч 1), так и от нижней (луч 2) грани клина (рис. 7). Лучи 1 и 2 когерентны между собой и интерферируют. Интерференционная картина представляет собой чередование темных и светлых полос. Темные полосы видны на тех участках клина, для которых оптическая разность хода кратна нечетному числу половины длины волны (условие минимума):
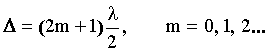
Оптическая разность хода в отраженном свете равна:
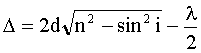
где i - угол падения луча. Так как по условию свет падает нормально, то i = 0 и sini = 0. Произвольной полосе с номером m соответствует толщина dm, а (m+1) полосе соответствует толщина клина dm+1 . Запишем условие минимума для двух соседних темных полос:
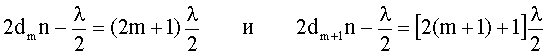
Отсюда:
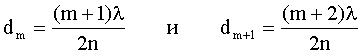
Тогда:
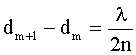
Из рисунка:
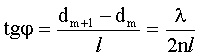
Вычислим:
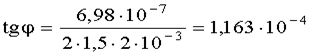
Тангенс мал, поэтому:
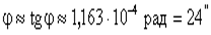
Ответ:
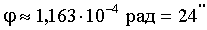
Задача 3. Измерение дисперсии показателя преломления оптического стекла дало n1 = 1,528 для λ1 = 0,434 мкм и n2 = 1,523 для λ2 = 0,486 мкм. Вычислить отношение групповой скорости к фазовой скорости для света с длиной волны 0,434 мкм.
Дано: |
|
Найти: |
|
Решение: Зависимость групповой скорости u от показателя преломления n и длины волны λ имеет вид:
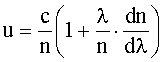 (1)
(1)
где с - скорость света в вакууме.
Фазовая скорость определяется как
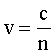 (2)
(2)
Разделив выражение (1) на (2), получим:
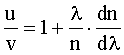
Средняя дисперсия:
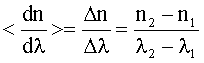
Для длины волны λ1 и средней дисперсии имеем:
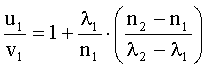
Вычисления:
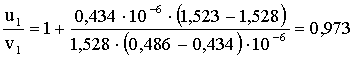
Ответ:
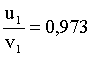
7 Примеры решения задач по квантовой физике
Задача 1. Найти длину волны де Бройля для электрона, кинетическая энергия которого равна: 1) 10 кэВ, 2) 1 МэВ.
Дано: |
|
Найти: |
|
Решение: Длина волны де Бройля связана с импульсом:
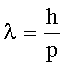
где
![]() - постоянная Планка; р - импульс частицы.
- постоянная Планка; р - импульс частицы.
Импульс частицы зависит от ее скорости. Если скорость движения частицы много меньше скорости света в вакууме (v<<c), то это случай нерелятивистский. Если скорость движения частицы соизмерима со скоростью света в вакууме, то это случай релятивистский. Импульс частицы связан с энергией. Поэтому, чтобы выяснить, какой это случай, вычислим энергию покоя частицы и сравним ее с энергией движущейся частицы. Вычислим энергию покоя электрона:
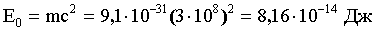
Сравним кинетическую энергию электрона с энергией покоя E0 . В первом случае W1<<E0, значит это случай нерелятивистский и импульс равен: p = mv. Импульс связан с кинетической энергией соотношением:
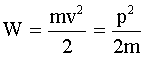
Отсюда:
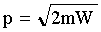
Тогда:
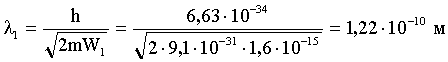
Во втором случае
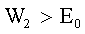 , значит это случай релятивистский. Импульс равен:
, значит это случай релятивистский. Импульс равен:  ,
,

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 |