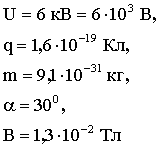Металлическая пластина является эквипотенциальной поверхностью. Поэтому силовые линии электрического поля перпендикулярны плоскости пластины. Тогда результирующее поле, созданное зарядом ![]() и индуцированным зарядом пластины, можно смоделировать и заменить электрическим полем, которой создается двумя точечными зарядами, один из которых заряд
и индуцированным зарядом пластины, можно смоделировать и заменить электрическим полем, которой создается двумя точечными зарядами, один из которых заряд ![]() , а второй – заряд противоположного знака, расположенный симметрично относительно пластины. Теперь рассмотрим решение отдельных условий задачи,
, а второй – заряд противоположного знака, расположенный симметрично относительно пластины. Теперь рассмотрим решение отдельных условий задачи,
1. В любой точке справа от пластины напряженность и потенциал электрического поля можно найти по формулам:
![]() ,
, ![]() (1)
(1)
В точке ![]() потенциал, созданный зарядом
потенциал, созданный зарядом ![]() , определяется по формуле потенциала поля точечного заряда:
, определяется по формуле потенциала поля точечного заряда:
![]() .
.
Потенциал, созданный зарядом ![]() , в этой же точке определяется по формуле:
, в этой же точке определяется по формуле:
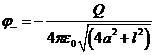 .
.
Теперь эти формулы подставим в формулу (1) и найдем потенциал в точке ![]() :
:
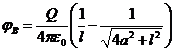 . (2)
. (2)
Размерность полученной величины можно проверить устно, так как известна формула потенциала точечного заряда. Теперь в последнюю формулу можно подставить численные значения и вычислить потенциал в точке ![]() :
: 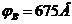 .
.
Так как пластина заземлена, то напряженность поля слева от пластины равна нулю, следовательно, потенциал в этих точках также будет равен нулю. Тогда ![]() .
.
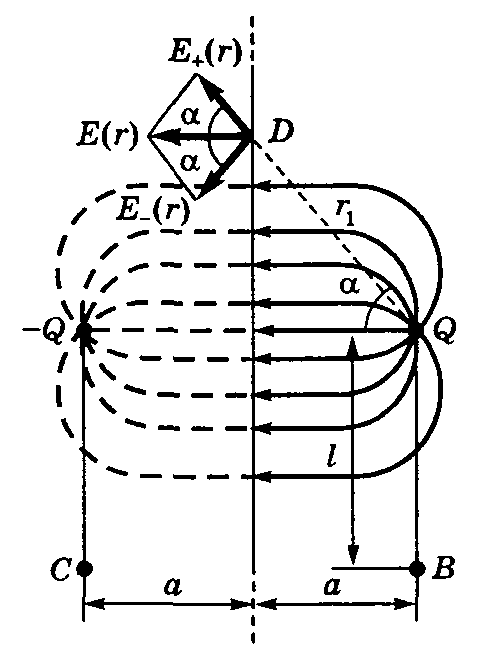
Рис.14
2. Чтобы определить поверхностную плотность ![]() в точке
в точке ![]() , надо определить напряженность поля в точке, близко подходящей к точке
, надо определить напряженность поля в точке, близко подходящей к точке ![]() , справа. Напряженность электрического поля в этой точке создается уже известными зарядами
, справа. Напряженность электрического поля в этой точке создается уже известными зарядами 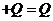 и
и ![]() . В силу симметричного расположения этих зарядов относительно металлической пластины и точки
. В силу симметричного расположения этих зарядов относительно металлической пластины и точки ![]() , для искомых напряженностей можно записать формулы:
, для искомых напряженностей можно записать формулы:
![]() . (3)
. (3)
Результирующий вектор напряженности должен быть направлен перпендикулярно металлической пластине. Тогда по правилу сложения векторов с учетом последнего выражения получим формулу для напряженности электрического поля в точке ![]() :
:
![]() .
.
Из теоремы Остроградского - Гаусса известно, что напряженность электрического поля у поверхности проводника определяется формулой:
![]() , где
, где ![]() - поверхностная плотность индуцированных зарядов.
- поверхностная плотность индуцированных зарядов.
Теперь из последних двух формул можно определить поверхностную плотность индуцированных зарядов в точке ![]() на пластине:
на пластине:
![]() . (4)
. (4)
Размерность полученной величины легко проверяется устно. Тогда можно подставить численные значения и вычислить поверхностную плотность заряда в точке ![]() :
: 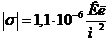 .
.
3. Из формулы поверхностной плотности заряда на пластине видно, что она зависит от расстояния ![]() от заряда
от заряда ![]() . Чтобы найти эту зависимость, из заряда
. Чтобы найти эту зависимость, из заряда ![]() проведем перпендикуляр к поверхности пластины. Точку пересечения этого перпендикуляра с поверхностью выберем как центр окружности радиуса
проведем перпендикуляр к поверхности пластины. Точку пересечения этого перпендикуляра с поверхностью выберем как центр окружности радиуса ![]() . Такая окружность будет множеством точек, равноудаленных от заряда
. Такая окружность будет множеством точек, равноудаленных от заряда ![]() . Эта ситуация изображена на рисунке 15.
. Эта ситуация изображена на рисунке 15.
Точки этой окружности имеют одинаковую поверхностную плотность заряда. Тогда чтобы найти суммарный индуцированный на пластине заряд, необходимо выделить элементарную площадку ![]() , в пределах которой поверхностную плотность заряда можно считать постоянной. Такой площадкой будет кольцо с радиусами
, в пределах которой поверхностную плотность заряда можно считать постоянной. Такой площадкой будет кольцо с радиусами ![]() и
и ![]() . Площадь такой площадки равна
. Площадь такой площадки равна ![]() , а расстояние от заряда до точек этой площадки равно
, а расстояние от заряда до точек этой площадки равно ![]() . Теперь используем формулу (4) и получим:
. Теперь используем формулу (4) и получим:
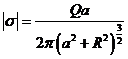 .
.
Тогда заряд площадки площадью ![]() равен:
равен: 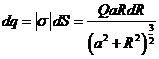 . Теперь чтобы найти величину заряда, необходимо проинтегрировать последнее выражение с учетом, что
. Теперь чтобы найти величину заряда, необходимо проинтегрировать последнее выражение с учетом, что ![]() изменяется от нуля до
изменяется от нуля до ![]() .
.
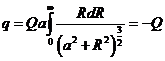 .
.
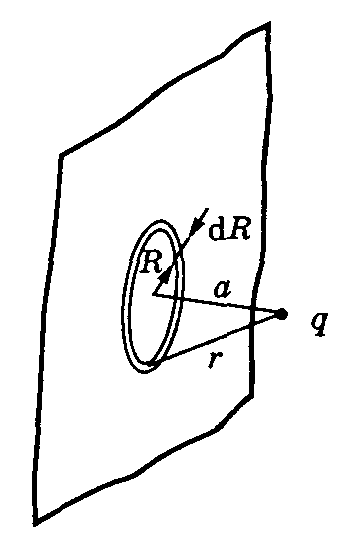
Рис.15
Таким образом, на пластине индуцирован заряд равный заряду ![]() , но противоположный по знаку.
, но противоположный по знаку.
Ответ: 1. ![]() ;
; ![]() ; 2.
; 2. ![]() ; 3.
; 3. ![]() .
.
Задача 12. Электрон, ускоренный разностью потенциалов 6 кВ, влетает в однородное магнитное поле под углом 300 к направлению поля и начинает двигаться по спирали. Индукция магнитного поля равна В =![]() .Найти радиус витка и шаг спирали.
.Найти радиус витка и шаг спирали.
Дано: |
|
Рис.4 |
Найти: | R, h. |
Решение: Скорость электрона найдем из условия, что работа сил электрического поля затрачивается на изменение кинетической энергии электрона:
А = ΔW. Работа в электрическом поле равна произведению заряда на разность потенциалов: А = qU. Начальная кинетическая энергия равна нулю, поэтому ΔW = W. Следовательно:
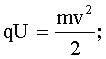 отсюда
отсюда 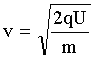 . (1)
. (1)
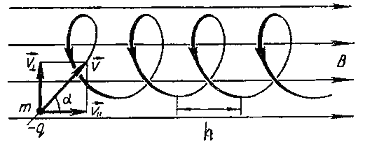
Разложим скорость электрона, влетающего в магнитное поле, на две составляющие:![]() - составляющая скорости, направленная вдоль силовых линий поля и
- составляющая скорости, направленная вдоль силовых линий поля и ![]() - составляющая скорости, направленная перпендикулярно силовым линиям поля. Из рис. 4:
- составляющая скорости, направленная перпендикулярно силовым линиям поля. Из рис. 4:

Проекция траектории электрона на плоскость, перпендикулярную к вектору ![]() , представляет собой окружность, следовательно, сила Лоренца сообщает частице нормальное (центростремительное) ускорение. Сила Лоренца равна:
, представляет собой окружность, следовательно, сила Лоренца сообщает частице нормальное (центростремительное) ускорение. Сила Лоренца равна:
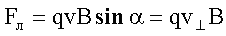

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 |