Потенциал φ результирующего поля в точке А по принципу суперпозиции для потенциала равен:
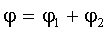
Потенциал поля, создаваемого точечным зарядом, равен:
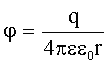
Но по условию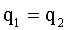 
. Тогда 
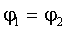, следовательно:
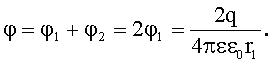
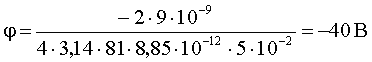
Проверка размерности:
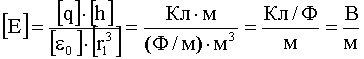
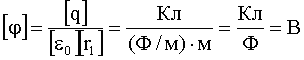
Ответ: Е = 480 В/м; φ = -40 В.
Задача 2. В вершинах квадрата, сторона которого равна а, расположены два положительных и два отрицательных заряда, значение каждого из них 
(рис.1, а, б). Определить напряженность электрического поля и потенциал в центре этого квадрата.
Решение: Поле создано четырьмя точечными зарядами. По условию задачи требуется найти характеристики поля в точке, которая равноудалена от всех четырех зарядов и лежит с ними в одной плоскости, т. е. находится в особых условиях по отношению к источникам поля. Поэтому и потенциал, и напряженность следует определять независимо друг от друга с помощью принципа суперпозиции:
(1)
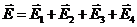(2)
При расчете потенциала знаки зарядов учитываются автоматически и, по-видимому, значение результирующего потенциала не зависит от порядка Рис. 1
расположения положительных и отрицательных зарядов в вершинах квадрата.
Чтобы рассчитать напряженность по формуле (2), следует показать сначала на рисунке направления всех векторов 
. зависящие от знака заряда . Очевидно, вектор напряженности 
зависит от порядка расположения зарядов в вершинах квадратов.
Расстояние от любого из зарядов до рассматриваемой точки равно
Потенциал, создаваемый точечным зарядом 
, в рассматриваемой точке, равен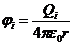 
. Следовательно, 
.
Так как, по условию задачи, алгебраическая сумма зарядов равна нулю, то и результирующий потенциал 
независимо от порядка расположения зарядов.
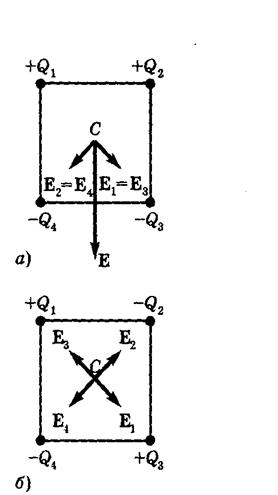
Рассмотрим распределение зарядов, показанное на рис. 1, а. Напряженности 
и 
полей, созданных 2-м и 4-м зарядами в точке С, имеют одинаковое направление и равны по модулю: 
Аналогично, 
. Поэтому напряженность результирующего поля можно определить по формуле
Векторы 
и также равны по модулю и направлены ортогонально друг другу (по диагоналям квадрата), значит, результирующий вектор направлен вертикально вниз (см. рис.1, а) и тогда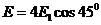 
.
Напряженность поля, созданного каждым из зарядов, определяется формулой:
Заряд следует брать по модулю, так как знак каждого из зарядов был учтен при изображении соответствующего вектора . Окончательно получаем
При расположении зарядов, показанном на рис. 1 б,
.
В данном случае расчетная формула соответствует формуле для определения напряженности поля точечного заряда, поэтому размерность можно проверить устно.
Ответ: а)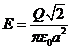 
; б) .
Задача 3. Два равных точечных заряда 
Кл находятся на расстоянии 10 см один от другого. Найти напряженность поля и потенциал в точках В и С (рис.2; 
см, 
см). Построить графики зависимости потенциала и напряженности от расстояния для точек, расположенных на линии, соединяющей заряды, и на перпендикуляре к ней, симметричном относительно зарядов.
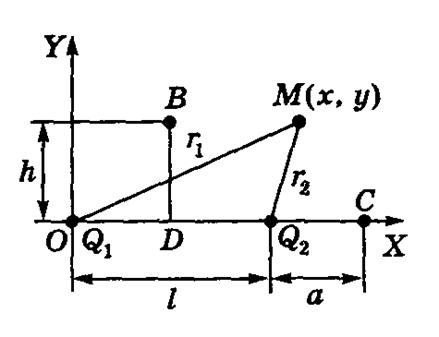
Рис.2
Решение: Электростатическое поле создается двумя точечными зарядами. В любой точке пространства потенциал результирующего поля может быть найден по принципу суперпозиции: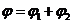 
, где 
и 
— потенциалы, созданные зарядами 
и 
соответственно. Рассмотрим некоторую произвольную точку 
и введем оси координат, показанные на рис.2. При таком выборе осей координат расстояния 
и 
от каждого из зарядов до точки 
можно записать в виде:
, 
.
Тогда потенциал точки можно найти по формуле:
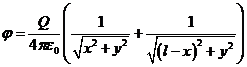(1)
Проекции вектора напряженности на оси координат находятся дифференцированием выражения (1) так как 
:
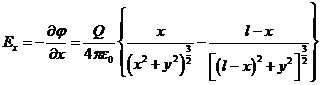
(2)
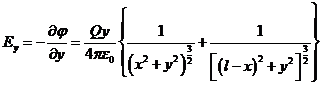
Выражения (2) позволяют найти модуль и направление вектора в любой точке.
Исследуя выражения (1) и (2), можно построить графики зависимости потенциала и проекций Ех и Еу от соответствующих координат.
Координаты точки
:
, 
. Координаты точки 
: 
,
. Подставляя их в выражения (1) и (2), находим потенциалы и проекции вектора напряженности в указанных точках.
В точке:
; 
; 
.
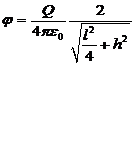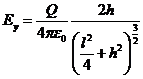Устно легко проверить размерность полученных величин и подставим численные значения. Тогда получим: 
; ; 
.
|
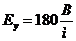Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
