Если заряд распределен по кольцу неравномерно, то выражения для потенциала и напряженности, определяемыми формулами (3) и (4), не изменятся, но проекции вектора напряженности электрического поля на оси ![]() и
и ![]() не будут равны нулю. В этом случае, чтобы найти
не будут равны нулю. В этом случае, чтобы найти ![]() и
и ![]() в точках, лежащих на оси
в точках, лежащих на оси ![]() , следует определить потенциал электрического поля в любой точке пространства, а затем дифференцированием получить выражения для проекций
, следует определить потенциал электрического поля в любой точке пространства, а затем дифференцированием получить выражения для проекций ![]() и
и ![]() . Чтобы найти эти величины в точках на оси кольца, надо в полученные выражения подставить значения
. Чтобы найти эти величины в точках на оси кольца, надо в полученные выражения подставить значения ![]() и
и ![]() .
.
Ответ: 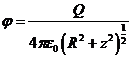 ,
, 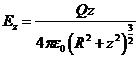 .
.
Задача 6. Длинный цилиндр радиусом 2 см заряжен положительным зарядом с объемной плотностью заряда 2 мкКл/м3. Найти напряженность поля в точках лежащих на расстояниях 1 см и 3 см от оси цилиндра, и разность потенциалов между этими точками. Построить графики зависимости напряженности и потенциала от расстояния от оси цилиндра.
Решение. Сделаем рисунок, соответствующей условию задачи.
Электрическое поле создано равномерно распределенным по цилиндру зарядом. Это позволяет сделать вывод о том, что поле обладает осевой симметрией: силовые линии этого поля – прямые, лежащие в плоскостях перпендикулярных оси цилиндра. Силовые линии этого поля направлены по радиусу цилиндра. Такое расположение силовых линий позволяет для решения задачи использовать теорему Остроградского – Гаусса.
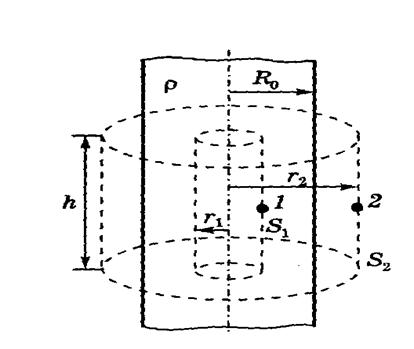
Рис.7
Для того, чтобы воспользоваться этой теоремой, выберем произвольную поверхность в форме цилиндра, ось которого совпадает с осью данного заряженного цилиндра, а высота меньше высоты заряженного цилиндра. В соответствии с условиями задачи выберем две поверхности, одна из которых ![]() имеет радиус равный
имеет радиус равный ![]() , а другая
, а другая ![]() имеет радиус
имеет радиус ![]() . Для каждой поверхности теорема Остроградского – Гаусса может быть записана в виде:
. Для каждой поверхности теорема Остроградского – Гаусса может быть записана в виде:
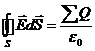 (1)
(1)
Так как вектор напряженности электрического поля и нормаль к основаниям цилиндров составляет угол 900, то поток через основания цилиндров равен нулю. Тогда при вычислении интеграла в формуле (1) необходимо вычислить только поток вектора напряженности электрического поля через боковую поверхность цилиндров. На боковых поверхностях цилиндров направление вектора напряженности совпадает с направлением вектора нормали к поверхности. Поэтому можно записать:
![]()
![]() (2)
(2)
где ![]() и
и ![]() - радиус и высота выбранных вспомогательных цилиндров. Теперь найдем суммарный заряд, который расположен внутри этих цилиндров.
- радиус и высота выбранных вспомогательных цилиндров. Теперь найдем суммарный заряд, который расположен внутри этих цилиндров.
В первом случае, когда ![]() суммарный заряд определяется формулой:
суммарный заряд определяется формулой:
![]() . (3)
. (3)
Здесь ![]() - расстояние от оси цилиндра до точки, в которой определяется напряженность электрического поля. Подставляя выражения (2) и (3) в формулу (1), получаем:
- расстояние от оси цилиндра до точки, в которой определяется напряженность электрического поля. Подставляя выражения (2) и (3) в формулу (1), получаем:
![]() , откуда следует формула напряженности электрического поля
, откуда следует формула напряженности электрического поля
![]() (4)
(4)
Если ![]() , то
, то ![]() . Подставляем это выражение и формулу (2) в формулу (1), получаем:
. Подставляем это выражение и формулу (2) в формулу (1), получаем: 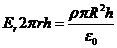 . Отсюда находим напряженность электрического поля в точках, в которых
. Отсюда находим напряженность электрического поля в точках, в которых ![]() :
:
![]() (5).
(5).
Проверяем размерность величин, полученных в формулах (4) и (5):
![]()
![]()
Теперь после проверки размерности можно подставить численные значения и получить результат:
При ![]()
![]() , а при
, а при ![]()
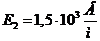 .
.
Чтобы найти разность потенциалов между указанными в задаче точками воспользуемся формулой:
![]() (6).
(6).
Для решения задачи интеграл в формуле (6) надо разбить на два интеграла: первый интеграл берется от точки ![]() до точки
до точки ![]() на поверхности заряженного цилиндра, а второй – от точки
на поверхности заряженного цилиндра, а второй – от точки ![]() до точки
до точки ![]() :
:
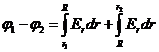 .
.
При вычислении этого интеграла в первый интеграл надо подставить формулу (4), а во второй – формулу (5), тогда:
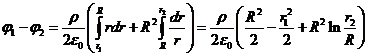 .
.
Проверим размерность полученной величины:
![]() .
.
Теперь можно подставить численные значения и вычислить разность потенциалов: ![]() .
.
Для построения графика зависимости напряженности от расстояния от оси цилиндра вычислим напряженность поля на поверхности цилиндра. Это позволяет определить точку, в которой функция зависимости напряженности от расстояния изменяет вид.
![]() .
.
Теперь можно построить график функции ![]() :
:
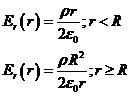 .
.
Принципиальный вид функции ![]() представлен на рисунке 8.
представлен на рисунке 8.
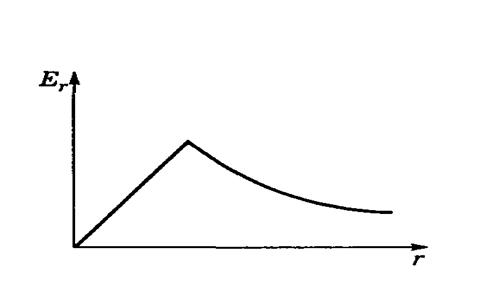
Рис.8
График зависимости ![]() можно построить из анализа графика функции
можно построить из анализа графика функции ![]() , учитывая, что
, учитывая, что ![]() . Зависимость
. Зависимость ![]() можно получить интегрированием последней формулы. При этом надо учесть наличие произвольной постоянной величины:
можно получить интегрированием последней формулы. При этом надо учесть наличие произвольной постоянной величины:
![]() .
.
Чтобы определить эту постоянную величину, надо задать начальные условия. В качестве начального условия можно выбрать значение потенциала в точках на оси цилиндра. Пусть, например, ![]() .
.
Так как во всей области напряженность больше нуля, то, как следует из формулы для потенциала, потенциал непрерывно убывает: 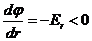 . Принципиальный график
. Принципиальный график ![]() представлен на рисунке 9. На этом же графике пунктиром показана зависимость потенциала от расстояния при выборе другого начального условия. Этот случай соответствует начальному условию
представлен на рисунке 9. На этом же графике пунктиром показана зависимость потенциала от расстояния при выборе другого начального условия. Этот случай соответствует начальному условию ![]() . При построении этого графика функция
. При построении этого графика функция ![]() исследовалась на определение точки перегиба и направление вогнутости на разных участках.
исследовалась на определение точки перегиба и направление вогнутости на разных участках.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 |





