Новые технологии в экономических информационных системах (стр. 21 )

3.Для расчета выручки и основной части зарплаты введем в ячейки D3 и ЕЗ соответственно формулы = ВЗ*СЗ и 10%*D3 и скопируем их в диапазоны D3:D202 и Е4:Е202.

4.Чтобы получить с помощью Генератора случайных чисел значения дискретной случайной величины, необходимо предварительно подготовить данные о ее ряде распределения. Для этого в диапазоне J3-J5 введены значения премии (в %), а в диапазоне КЗ:К5 - их вероятности. После вызова Генерации случайных чисел необходимо выбрать: Распределение - Дискретное. Входной интервал значений и вероятностей - $J$3:$K$5. Выходной интервал - $G$3.

5.  В ячейку НЗ введем формулу =ЕЗ*(1+GЗ) и скопируем ее в диапазон Н4:Н202.

6.  Найдем M(Z) и σ(Z) с помощью формул, представленных в таблице 3.34.

Таблица 3.34 – Расчет показателей

7 Чтобы проследить влияние σ(С) на M(Z) и σ(Z) удобнее всего скопировать полученные расчеты на новые листы, где в диапазонах СЗ:С202 сгенерировать значения рыночной цены при других значениях σ(С). Нетрудно заметить, что при изменении σ(С) практически не изменяется M(Z), в то же время с увеличением σ(С) растет и σ(Z).

Контрольные вопросы

1.  Как работает генератор случайных чисел?

2.  Что необходимо указать генератору при нормальном распределении?

3.  Какие данные необходимы при биноминальном распределении?

Практическая работа № 21

Корреляционный анализ

Задание

Необходимо выяснить, имеется ли взаимосвязь показателей эффективности производства продукции на машиностроительных предприятиях в целом по группе однотипных производств. В качестве показателей оценки эффективности были выбраны следующие факторы: производительность труда, фондоотдача, материалоемкость продукции. Статистическая информация о динамике и значениях этих показателей была собрана по отрасли машиностроения, из которой в качестве статистической выборки была отобрана для анализа группа из 25 однотипных машиностроительных предприятий.

Методика выполнения практической работы

На основании исследования годовых отчетов предприятий были получены данные, представленные в таблице 3.35:

х - выработка валовой продукции в неизменных ценах на одного работающего средней списочной численности ППП, млн. руб.;

у - выпуск валовой продукции на 1 руб. среднегодовой стоимости основных промышленно-производственных фондов, руб.;

z - материалоемкость в стоимостном выражении: стоимость материалов в валовой продукции в неизменных ценах, %.

Для проведения корреляционного анализа можно использовать модуль Анализ данных режима меню-системы Сервис в котором необходимо активизировать инструмент анализа Корреляция. При этом откроется диалоговое окно Корреляция, в котором необходимо заполнить предлагаемые поля.

Таблица 3.35- Исходные данные к задаче

Порядок заполнения может быть следующим.

Входной диапазон. Вводится ссылка на диапазон ячеек $B$2:$D$26, содержащие анализируемые данные.

Примечание. Ссылка должна состоять как минимум из двух смежных диапазонов данных, организованных в виде столбцов или строк.

Выходной диапазон. Вводится ссылка на левую верхнюю ячейку выходного диапазона $Е$7.

Примечание. Поскольку коэффициент корреляции двух наборов данных не зависит от последовательности их обработки, то выходная область занимает только половину предназначенного для нее места. Ячейки выходного Диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждая строка или столбец во входном диапазоне полностью коррелирует с самим собой.

Группирование. Для этого необходимо установить переключатель в положение по столбцам и нажать ОК.

Из полученных расчетов видно, что поддиагональные элементы представляют собой не что иное, как парные коэффициенты корреляции: rxy, rxz, rvz.

Известно, что коэффициент корреляции принимает значения из интервала от -1 до + 1.

Значения +1 коэффициент корреляции достигает в том случае, если между соответствующими отклонениями (хi -) и (yi -) существует прямая связь, а значения -1, - если между ними существует обратная связь. Чем больше значение связи между этими величинами отклоняется от прямой или обратной, тем больше сумма отклонений приближается к нулю.

При положительном коэффициенте корреляции говорят о положительной корреляции, при отрицательном - об отрицательной корреляции. Чем ближе коэффициент корреляции к значению ±1, тем теснее и интенсивнее связь. При линейновозрастающей функциональной зависимости между переменными у и х rух=+ 1, при линейноубывающей ryx= -1. Чем ближе коэффициент корреляции приближается к нулю, тем слабее исследуемая связь. В случае линейной связи между двумя переменными имеется только один коэффициент корреляции.

Для вычисления коэффициента корреляции между двумя наборами данных можно воспользоваться статистической функцией КОРРЕЛ.

Ввести в ячейки формулы:

rxy V15: =КОРРЕЛ (В1:В26;С1:С26);

rxz V16: =КОРРЕЛ (В1:В26;D1:D26);

rvz V17: =КОРРЕЛ (С1:С26;D1:D26).

Для этого воспользуемся мастером функций, выбрав в окне Мастер функций категорию Статистические, а в ней - функцию КОРРЕЛ.

Где массив1 – ячейка интервала значений; массив 2 - второй интервал ячеек со значениями.

Данная функция возвращает коэффициент корреляции между интервалами ячеек определенных по адресам массив! и массие2. Коэффициент корреляции используется для определения наличия взаимосвязи между двумя свойствами.

На основании полученных расчетов можно сделать следующие выводы.

Доказана тесная взаимосвязь каждого из исследуемых показателей эффективности работы предприятия с другими (все множественные коэффициенты детерминации значимы и превышают 0,8).

Особенно тесная связь существует между фондоотдачей и двумя остальными показателями - производительностью труда и материалоемкостью. Изменение фондоотдачи в среднем на 84,25 % объясняется изменением производительности труда и материалоемкости (изменение фондоотдачи в среднем на 15,75 % объясняется влиянием неконтролируемых факторов, признаков). При этом при увеличении производительности труда на I млн. руб. фондоотдача увеличивается в среднем на 0,55 руб. на рубль основных производственных фондов. При уменьшении материалоемкости на 1 % фондоотдача увеличивается в среднем на 0,48 %. Указанные нормативы относительно стабильны при условии, что изучаемые показатели отклоняются на небольшие величины от своих средних уровней (стабильность указывается доверительными интервалами и вероятностью 0,95).

Взаимозависимость между материалоемкостью и производительностью труда (без учета фондоотдачи) не доказана (частный коэффициент корреляции pxz/y незначим) при данных условиях. Для более надежной проверки такой зависимости необходим значительно больший объем выборки, чем имеющийся у нас.

Контрольные вопросы

1.  Как организуются данные при проведении корреляционного анализа?

2.  В каких случаях используется корреляционный анализ?

3.  Какие функции участвуют в проведении корреляционного анализа?

Практическая работа № 22

Регрессионный анализ

Задание

Решить задачу построения регрессионной модели. С помощью средства поиска решений решить задачу нахождения уравнения регрессии для одной зависимой и одной независимой переменных.

Методика выполнения работы

Имеются две наблюдаемые величины х и у, например, объем реализации фирмы, торгующей подержанными автомобилями, за шесть недель ее работы. Значения этих наблюдаемых величин приведены на рисунке 3.29, где х — отчетная неделя, а у — объем реализации за эту неделю.

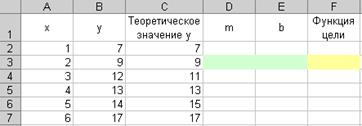
Рисунок 3.29 - Исходные данные для построения линейной модели

Необходимо построить линейную модель , наилучшим образом описывающую наблюдаемые значения. Обычно т и b подбираются так, чтобы минимизировать сумму квадратов разностей между наблюдаемыми и теоретическими значениями зависимой переменной у, то есть минимизировать

, (3.4)

где n — число наблюдений (в данном случае n = 6).

Для решения этой задачи отведем под переменные m и b ячейки D3 и ЕЗ, соответственно, а в ячейку F3 введем минимизируемую функцию {=СУММКВРАЗН(В2:В7;E3+D3*A2:А7)}.

Функция суммквразн вычисляет сумму квадратов разностей для элементов указанных массивов.

Теперь выберем команду Сервис, Поиск решения и заполним открывшееся диалоговое окно Поиск решения, как показано на рисунке 3.30.

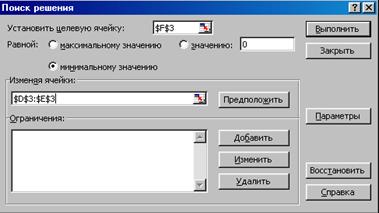
Рисунок 3.30 - Диалоговое окно Поиск решения для расчета уравнения регрессии

Отметим, что на переменные т и b ограничения не налагаются. В результате вычислений средство поиска решений найдет: т = 1,88571 и b = 5,400. Данные результаты приведены на рисунке 3.31.

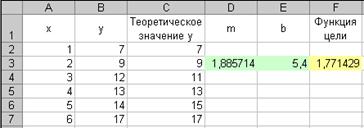
Рисунок 3.31 – Оптимальное решение уравнения регрессии

В данном разделе приведены функции рабочего листа, непосредственно вычисляющие различные характеристики линейного уравнения регрессии,

Параметры т и b линейной модели из предыдущего раздела можно определить с помощью функций наклон и отрезок.

Наклон — это скорость изменения значений вдоль прямой. Функция наклон определяет коэффициент наклона линейного тренда. Синтаксис:

НАКЛОН (известные_значения_у; известные_значения х).

Функция отрезок (intercept) определяет точку пересечения линии линейного тренда с осью ординат.

Синтаксис:

ОТРЕЗОК (известные_значеыия_х; известные_значения_у).

Аргументы функций наклон и отрезок:

-  известные_значения_у - массив известных значений зависимой наблюдаемой величины;

-  известные_значения_х – массив известных значений независимой наблюдаемой величины. Если аргумент известные_значения_х опущен, то предполагается, что это массив {1;2;3;…} такого же размера, как и аргумент известные_значения__у

Функции наклон и отрезок вычисляются по следующим формулам:

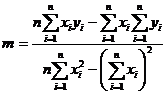, (3.5)

, (3.6)

где ,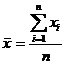

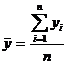
В ячейках D2 и Е2, найдены т и b, соответственно, по формулам:

=НАКЛОН(В2:В7;А2:А7);

=ОТРЕЗОК(В2:В7;А2:А7).

Коэффициенты т и b можно найти и другим способом. Постройте точечный график по диапазону ячеек А2:В7, выделите точки графика двойным щелчком, а затем щелкните их правой кнопкой мыши. В раскрывшемся контекстном меню выберите команду Линии тренда, как показано на рисунке 3.32.

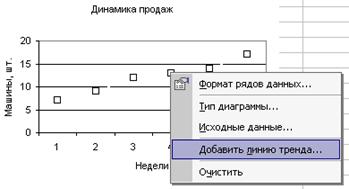
Рисунок 3.32 - Начало построения линии тренда

В диалоговом окне Линия тренда на вкладке Тип в группе Построение линии тренда (аппроксимация и сглаживание) выберите параметр Линейная, а на вкладке Параметры установите флажки Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации (R^2) (то есть на диаграмму необходимо поместить значение квадрата коэффициента корреляции).

По коэффициенту корреляции можно судить о правомерности использования линейного уравнения регрессии. Если он лежит в диапазоне от 0,9 до 1, то данную зависимость можно использовать для предсказания результата. Чем ближе к единице коэффициент корреляции, тем более обоснованно это указывает на линейную зависимость между наблюдаемыми величинами. Если коэффициент корреляции близок к -1, то это говорит об обратной зависимости между наблюдаемыми величинами.

Флажок Пересечение кривой с осью Y в точке, устанавливается только в случае, если эта точка известна. Например, если этот флажок установлен и в его поле введен 0, это означает, что ищется модель .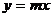

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28