Новые технологии в экономических информационных системах (стр. 16 )

Методика выполнения практической части работы

Вначале следует заполнить таблицу 3.18.

Таблица 3.18 – Исходные данные

В столбцы А, В, С, Е и Н этой таблицы следует ввести необходимые данные.

Далее ячейке НЗ желательно присвоить имя (Вставка→Имя→Присвоить), например «ЗС». (Это абсолютная адресация, удобно для копирования).

В ячейку D3 вносим формулу =A3*ЗС + B3, где ЗС - зарплата санитарки (Если ячейке НЗ не присваивать имя, то формула будет такой: =А3*$Н$3+ВЗ). Размножим формулу до конца данных в столбце D

Щелкнем по ячейке F3. Введем в нее формулу =D3*E3. Размножим эту формулу до ячейки F10.

В ячейку F12 введем формулу =СУММ(FЗ:F10). Попробуйте сделать это при помощи значка «Автосумма»

Данные в столбце «Количество сотрудников»отмечены данные, которые не могут быть изменены. Мы видим, что суммарный месячный фонд зарплаты превышает $10000.

А теперь заставим Excel проделать эту работу за нас:

Щелкните по ячейке F12. Выберите Сервис→ Подбор Параметра. В появившемся диалоговом окне необходимо установить в поле ввода «Установит ячейке» - значение $F$12; в поле ввода «Значение» - 10000; в поле ввода «Изменяя ячейку значение $Н$3 и нажать Ok. Мы увидим в Н3, какой должна быть зарплата санитарки.

Составьте и просчитайте на этом же листе еще вариант таблицы со следующим количеством сотрудников: Санитарок - 7, медсестер -10, врачей -12

Практическая работа № 12

Изучение финансовых функций. Механизмы вычислений, форматы данных, синтаксис функций

Excel предоставляет большой спектр функций финансового анализа
: от нахождения платы по процентам, амортизации оборудования, регулярных выплат по займу до оценки эффективности капиталовложений.

Данные функции вызываются командой Вставка, Функции или нажатием кнопки Мастер функций. Далее устанавливается категория Финансовые и в списке выбирается нужная функция, как показано на рисунке 3.3.

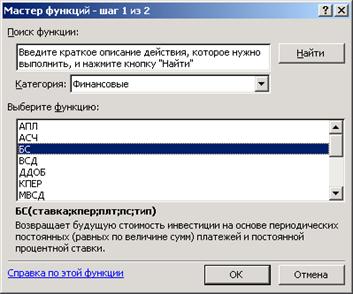
Рисунок 3.3 – Окно Мастер функций

Финансовая функция БС (БЗ), изображенная на рисунке 3.4, позволяет рассчитать будущее значение вклада (инвестиций) на основе периодических постоянных платежей и постоянной процентной ставки. Функция БС подходит для расчета итогов накоплений при ежемесячных банковских взносах.

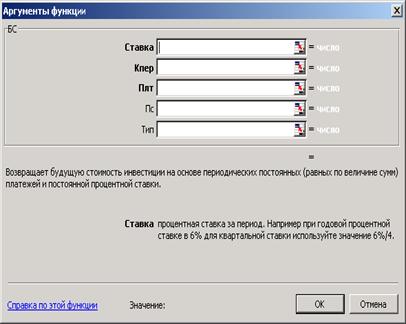
Рисунок 3.4 – Диалоговое окно функции БС

Синтаксис: БС (ставка; кпер; выплата; нз; тип).

Аргументы:

-  ставка - процентная ставка за период;

-  кпер - общее число периодов выплат;

-  плт (выплата) - величина постоянных периодических платежей;

-  нз - текущее значение, то есть общая сумма, которую составят будущие платежи;

-  тип - число 0 или 1, обозначающее, когда должна производиться выплата. Если тип равен 0 или опущен, то оплата производится в конце периода, если 1 – в начале периода.

Очень важно быть последовательным в выборе единиц измерения для задания аргументов «ставка» и «кпер». Так как в большинстве случаев, если это специально не оговорено, процентная ставка является годовой и срок вклада или займа исчисляется в годах, то при ежемесячном (ежеквартальном, полугодовом, ежедневном и т. д.) начислении процентов при задании аргумента «ставка» необходимо годовую процентную ставку разделить на число периодов в году, а при задании аргумента «кпер» количество лет, наоборот, умножить на это число. Например, если производятся ежемесячные выплаты по четырехгодичному займу из расчета 12 % годовых, то для задания аргумента «ставка» используется 12 %/12, а для задания аргумента «кпер» – 4*12. Если же производятся ежегодные платежи по тому же займу, то для задания аргумента «ставка» используется 12 %, а для задания аргумента «кпер» – 4.

В функциях, связанных с интервалами выплат, выплачиваемые деньги представляются отрицательным числом, а получаемые деньги представляются положительным числом. Например, депозит в банк на сумму 1000 тенге представляется аргументом -1000, если расчеты ведутся со стороны вкладчика, и аргументом 1000, если расчеты ведутся от представителя банка.

Рассмотрим пример использования функции БЗ. Необходимо рассчитать, какая сумма будет на счете, если 3 млн. тенге размещены под 12 % годовых на пять лет, и проценты начисляются каждый месяц. Будущая стоимость вычисляется следующим способом:

=БС(12%/12;5*12;;).

Через пять лет на счете будет 5450090 тенге.

Задачи для решения по функции БС.

Финансовая функция ПЗ (ПС), отображенная на рисунке 3.5, предназначена для расчета текущей стоимости как единой суммы вклада (займа), так и будущих платежей (фиксированных и периодических). Этот расчет является обратным к определению будущей стоимости функцией БЗ.

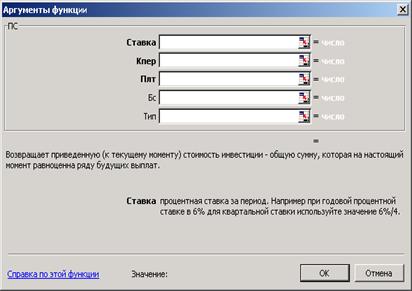
Рисунок 3.5 – Диалоговое окно функции ПЗ (ПС)

Синтаксис: ПЗ (ставка; кпер; плт; бс; тип).

Все значения аргументов совпадают с аргументами функции БЗ. Аргумент «бс» означает будущую стоимость или баланс, который нужно достичь после последней выплаты.

Рассмотрим пример решения задачи с помощью функции ПЗ. Необходимо определить, какую сумму нужно положить на депозит в настоящее время, чтобы при ставке 11,5 % годовых и ежемесячных вкладах на данный депозит в размере 1500 тенге через пять лет получить 100 тысяч тенге.

Используя функцию ПЗ, получим:

=ПЗ(11,5%/12;5*12;-1500;100000).

Ответ: в настоящее время на депозит нужно положить 11780 тенге.

Задачи для решения по функции ПС

Финансовая функция ЧПС (НПЗ) вычисляет чистую текущую (приведенную) стоимость периодических платежей переменной величины как сумму ожидаемых доходов и расходов, дисконтированных
нормой процента. Чистый текущий объем вклада – это сегодняшний объем будущих платежей (отрицательные значения) и поступлений (положительные значения).

Окно данной функции показано на рисунке 3.6.

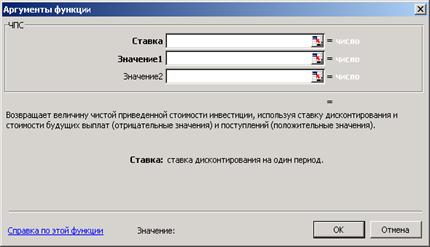
Рисунок 3.6 – Диалоговое окно функции ЧПС (НПЗ)

Синтаксис: ЧПС (норма; значение1; значение2; …; значение29).

Аргументы:

-  норма – норма скидки за один период;

-  значение1, …, значение29 – от 1 до 29 аргументов, представляющих расходы и доходы в конце каждого периода.

Считается, что инвестиция, значение которой вычисляет функция ЧПС, начинается за один период до даты денежного взноса первого значения и заканчивается с последним денежным взносом в списке. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС, но не включать в список аргументов. Вычисления функции ЧПС базируются на будущих денежных взносах.

Функция ПС аналогична функции ЧПС. Основное различие между ними заключается в том, что функция ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода' Кроме того, в отличие от функции ЧПС, денежные взносы в функции ПС должны быть постоянными и равными на весь период инвестиции, тогда как функция ЧПС допускает неодинаковые значения.

Рассмотрим пример использования функции ЧПС (НПЗ). Затраты по проекту в начальный момент его реализации составляют 37 миллионов тенге, а ожидаемые доходы за первые пять лет – 8, 9,2, 10, 13,9 и 14,5 миллионов. На шестой год ожидается убыток в размере 6,5 миллионов тенге. Цена капитала – 8 % годовых. Необходимо рассчитать чистую текущую стоимость проекта.

Настоящее приведенное значение рассчитывается следующим способом:

=ЧПС(8%;8;9,2;10;13,9;14,5;-6,5).

В результате чистая текущая стоимость проекта составит округленно 39,2 миллиона тенге. Исходя из этой суммы, можно предположить, что данный проект достаточно выгоден для вложения капитала.

Задачи для решения по функции ЧПС

Финансовая функция КПЕР, изображенная на рисунке 3.7, используется для расчета срока платежей. Эта функция вычисляет общее число периодов выплат как единой суммы вклада, так и для периодических постоянных выплат на основе постоянной процентной ставки.

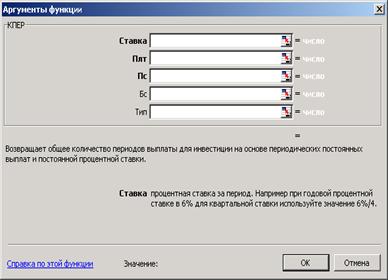
Рисунок 3.7 – Диалоговое окно функции КПЕР

Синтаксис: КПЕР (ставка; выплата; нз; бз; тип).

Все значения аргументов данной функции совпадают со значениями предыдущих финансовых функций.

Рассмотрим следующий пример: предприниматель берет кредит в 100000 тенге при годовой ставке 12 % и собирается выплачивать по 2000 тенге в месяц. Число выплат вычисляется следующим образом:

=КПЕР(12%/12;-2000;100000;0;1).

Срок выплаты кредита составит округленно 69 месяцев или 5,7 лет.

Для данной функции существенно, когда должна производиться выплата – в начале или в конце периода. Если в предыдущем примере в графе «тип» поставить 0, то срок составит округленно 70 месяцев или 5,8 лет.

Задачи для решения по функции КПЕР

Функция СТАВКА (НОРМА) вычисляет процентную ставку за один период, необходимую для получения определенной суммы в течение заданного срока путем постоянных взносов. Диалоговое окно данной функции представлено на рисунке 3.8

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28