Новые технологии в экономических информационных системах (стр. 17 )

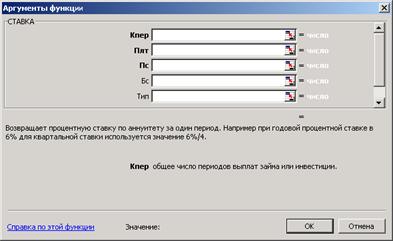
Рисунок 3.8 – Диалоговое окно функции Ставка

Синтаксис: СТАВКА(кпер; плт; пс;. бс; тип; предположение).

Все значения аргументов данной функции совпадают со значениями предыдущих финансовых функций. Аргумент «предположение» («нач_прибл») - предполагаемая величина нормы. Если «предположение» опущено, то оно полагается равным 10%. Если функция СТАВКА не сходится, следует попытаться использовать различные значения «нач_прибл». Обычно функция СТАВКА сходится, если «нач_прибл» имеет значение между 0 и 1.

Следует отметить, что функция СТАВКА вычисляет процентную ставку методом итераций, поэтому решение может быть и не найдено. Если после 20 итераций погрешность определения ставки превышает 0,0 то функция СТАВКА возвращает значение ошибки #ЧИСЛО!.

Рассмотрим пример использования функции СТАВКА. Чтобы определить процентную ставку для четырехлетнего займа размером в 8000 тенге с ежемесячной выплатой 200 тенге, можно использовать формулу:

=СТАВКА(4*12;-200;8000).

В результате получаем: месячная (так как период равен месяцу) процентная ставка равна 0,77 %.

Задачи для решения по функции СТАВКА

Финансовая функция БЗРАСПИС вычисляет будущее значение инвестиций после начисления сложных процентов при переменной процентной ставке. Диалоговое окно данной функции представлено на рисунке 3.9.

Рисунок 3.9 – Диалоговое окно функции БЗРАСПИС

Синтаксис: БЗРАСПИС (первичное; план).

Аргументы:

-  первичное - текущее значение вклада (инвестиций);

-  план – массив применяемых процентных ставок.

Если данная функция недоступна или возвращает ошибку #ИМЯ?, необходимо установить и загрузить надстройку «Пакет анализа» (меню Сервис → Надстройки → Пакет анализа).

Рассмотрим пример использования финансовой функции БЗРАСПИС. По облигации номиналом 100 тысяч тенге, выпущенной на 6 лет, предусмотрен следующий порядок начисления процентов: в 1 год – 10 %, 2, 3 - по 20 %, 4, 5, 6 – по 25 %. Рассчитать будущую (наращенную) стоимость облигации по сложной процентной ставке.

Для решения данной задачи необходимо занести все процентные ставки на рабочий лист, как показано на рисунке 3.10. Далее в графу «первичное» заносится номинальная стоимость облигации, а в графу «план» - массив процентных ставок из диапазона B1:B6.

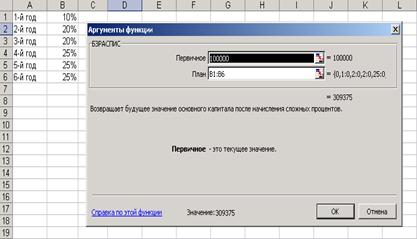
Рисунок 3.10 – Пример использования функции БЗРАСПИС

Будущая стоимость облигации через шесть лет составит 309375 тенге.

Задачи для решения

Функция ВНДОХ (ВСД), представленная на рисунке 3.11, возвращает внутреннюю скорость оборота для ряда потоков денежных средств. Объемы операций не обязаны быть регулярными, как в случае ренты. Внутренняя скорость оборота – это процентная ставка дохода, полученного от инвестиций, состоящих из выплат (отрицательные значения) и поступлений (положительные значения), которые происходят в регулярные периоды времени.

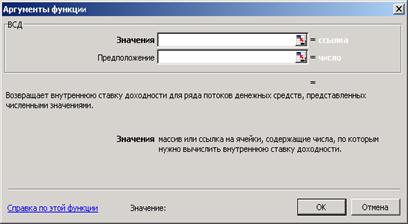
Рисунок 3.11 – Диалоговое окно функции ВНДОХ (ВСД)

Синтаксис: ВНДОХ (значения; предположение).

Аргументы:

-  значения - массив или ссылка на ячейки, содержащие числовые величины, для которых вычисляется внутренняя скорость оборота средств. Значения должны включать, по крайней мере, одно положительное значение и одно отрицательное значение, для того чтобы можно было вычислить внутреннюю скорость оборота. Функция ВНДОХ, использует порядок значений для интерпретации порядка денежных выплат или поступлений, поэтому нужно следить, чтобы значения выплат и поступлений вводились в правильном порядке;

-  предположение - величина, о которой предполагается, что она близка к результату ВНДОХ.

Для вычисления ВНДОХ Excel использует метод итераций. Начиная со значения прогноз, функция ВНДОХ выполняет циклические вычисления, пока не получит результат с точностью 0,00001. Если функция ВНДОХ не может получить результат после 20 попыток, возвращается значение ошибки #ЧИСЛО!.

В большинстве случаев нет необходимости задавать предположение для вычислений с помощью функции ВНДОХ. Если предположение опущено, то оно полагается равным 0,1 (10%).

Если ВНДОХ выдает значение ошибки #ЧИСЛО! или результат далек от ожидаемого, можно попытаться выполнить вычисления еще раз, но уже с другим предположением.

Рассмотрим пример использования функции ВНДОХ. Предположим, вы хотите открыть обменный пункт. Вы вносите первоначальную сумму для организации бизнеса в 50 тысяч долларов и ожидаете получить чистый доход в течение 5 лет в следующих размерах: 1-й год – 12; 2-й год – 13; 3-й год – 15; 4-й год – 17; 5-й год – 18 тысяч долларов. Вычислить внутреннюю скорость оборота инвестиций (процентная ставка дохода от вложенного капитала) после двух, трех, четырех и пяти лет. Решение данной задачи представлено на рисунке 3.12.

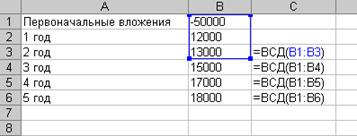
Рисунок 3.12 – Пример использования функции ВНДОХ (ВСД)

Внутренняя скорость оборота инвестиций после двух, трех, четырех и пяти лет составит -36 %, -10 %, 5 % и 14 % соответственно.

Задачи для решения.

Практическая работа № 13

Схема погашения кредита

Функция ППЛАТ (ПЛТ) вычисляет величину постоянной периодической выплаты ренты (например, регулярных платежей по займу) при постоянной процентной ставке. Диалоговое окно данной функции отображено на рисунке 3.13.

Синтаксис: ППЛАТ (ставка; кпер; нз; бз; тип).

Все значения аргументов финансовой функции ППЛАТ совпадают со значениями аргументов предыдущих функций.

Для нахождения общей суммы, выплачиваемой на протяжении интервала выплат, необходимо умножить возвращаемое функцией ППЛАТ значение на величину «кпер».

Рисунок 3.13 – Диалоговое окно функции ППЛАТ (ПЛТ)

Функция ОСНПЛАТ (ОСПЛТ) возвращает величину выплаты за данный период на основе периодических постоянных платежей и постоянной процентной ставки. Диалоговое окно данной функции представлено на рисунке 3.14.

Рисунок 3.14 – Диалоговое окно функции ОСНПЛАТ (ОСПЛТ)

Синтаксис: ОСНПЛАТ(ставка; период; кпер; нз; бз; тип)

Функция ПЛПРОЦ (ПРПЛТ), представленная на рисунке 3.15, возвращает платежи по процентам за данный период на основе периодических постоянных выплат и постоянной процентной ставки.

Синтаксис: ПЛПРОЦ(ставка; период; кпер; нз; бз; тип).

Рисунок 3.15 – Диалоговое окно функции ПЛПРОЦ (ПРПЛТ)

Аргументы функций ПЛПРОЦ и ОСНПЛАТ:

-  ставка - процентная ставка за период;

-  период - период, за который требуется найти прибыль (должен находиться в интервале от 1 до «кпер»);

-  кпер - общее число периодов выплат;

-  нз - текущее значение, то есть общая сумма, которую составят будущие платежи;

-  бз - будущая стоимость или баланс наличности, который нужно достичь после последней выплаты. Если аргумент «бз» опущен, он полагается равным 0 (например, будущая стоимость займа равна 0);

-  тип - число 0 или 1, обозначающее, когда должна производиться выплата. Если тип равен 0 или опущен, то оплата производится в конце периода, если 1 – то в начале периода

Рассмотрим пример вычисления основных платежей, платы по процентам, общей ежегодной платы и остатка долга на примере ссуды размером в 100000 тенге на срок 5 лет при годовой ставке 2 %. Схему погашения кредита можно представить в виде таблицы, приведенной на рисунке 3.16.

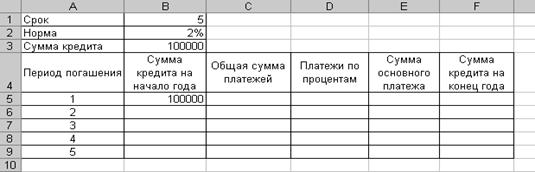
Рисунок 3.16 – Схема погашения кредита

Перед решением задачи необходимо присвоить ячейкам B1, B2 и B3 имена «Срок», «Процент» и «Сумма_кредита» соответственно. Имя – это слово или набор символов, представляющих ячейку, диапазон ячеек, формулу или константу. В данном случае срок кредита, процентная ставка и сумма выступают в роли неизменных констант. Поэтому, например, имя «Процент», которому присвоено значение 2 %, можно использовать в любом месте для вычисления процентов. К тому же определенное имя в формуле облегчает понимание назначения формулы.

По умолчанию имена являются абсолютными ссылками на ячейку. Абсолютный адрес ячейки – это часть формулы, являющаяся адресом ячейки и ссылающаяся на данную ячейку независимо от местоположения ячейки с формулой. Абсолютный адрес ячейки имеет формат $A$1. Если же данной ячейке присвоено имя, то оно будет отображаться в формуле вместо адреса ячейки.

Первый знак в имени должен быть буквой или знаком подчеркивания. Остальные знаки имени могут быть: буквами, числами, точками и знаками подчеркивания. Пробелы недопустимы.

Присвоение имени ячейке осуществляется с помощью команды Вставка → Имя → Присвоить.

В ячейке B5 ставится сумма кредита на начало первого года – 100000 тенге.

В ячейке C5 необходимо вычислить общую сумму платежей за год. Для этого вызывается функция ПЛТ (ППЛАТ) и заполняется, как показано на рисунке 3.17.

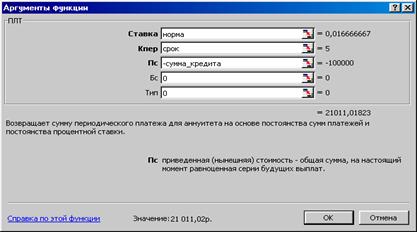
Рисунок 3.17 – Заполнение функции ПЛТ

Платежи по процентам за первый год в ячейке D5 вычисляются с помощью финансовой функции ПРПЛТ (ПЛПРОЦ), как показано на рисунке 3.18.

В графе «период» ставится ссылка на ячейку A5 с номером текущего периода, причем данная ссылка является относительной, то есть она может изменяться в зависимости от местоположения формулы.

Сумма основного платежа за первый год в ячейке E5 вычисляется с помощью функции ОСПЛТ (ОСНПЛАТ), как показано на рисунке 3.19.

Сумма кредита на конец первого года определяется как разность суммы кредита на начало первого года и суммы основного платежа за первый год.

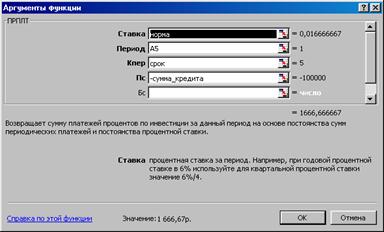
Рисунок 3.18 – Определение суммы платежей по процентам

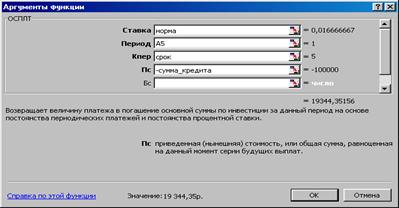
Рисунок 3.19 – Вычисление суммы основного платежа

Сумма кредита на начало второго года равна сумме кредита на конец первого года. Поэтому в ячейке B6 указывается ссылка на ячейку F5. В оставшиеся годы суммы кредита определяются путем протаскивания маркера заполнения ячейки F5 вниз по столбцу.

Общая сумма платежей, платежи по процентам, сумма основного платежа и сумма кредита на конец оставшихся периодов заполняются аналогично путем протаскивания маркера заполнения выделенного диапазона C5:F5 вниз по столбцам.

Задача 1. Составить схему погашения кредита при исходных данных, представленных в таблице 3.18.

Таблица 3.18 – Исходные данные

При выполнении задачи необходимо исходным данным присвоить имена (абсолютную адресацию), используя средства «Вставка» → «Имя» →»Присвоить».

Общую сумму платежа необходимо вычислить при использовании финансовой функции ППЛАТ.

Сумма платежа по процентам вычисляется при использовании функции ПЛПРОЦ

Сумма платежа основного долга вычисляется при помощи функции ОСНПЛАТ.

Сумма долга на конец периода вычисляется как сумма долга на начало периода минус сумма платежа основного долга.

Сумма долга на начало периода переносится из ячейки таблицы, которая содержит сумму долга на конец предыдущего периода.

Задача 2. Разработать схему погашения кредита на сумму 250000 выданную на один год под 28% годовых, при ежемесячном погашении.

Задача 3. Разработать схему погашения кредита размером 800000 выданного на 3 года под 20% годовых с ежеквартальным погашением.

Выполняя задачи 2и 3 необходимо присваивать имена исходным данным. Имена клеток не должны содержать пробелы. (пример имени Срок1, Норма2 и т. д.)

Практическая работа № 14

Финансовые функции в сочетании

1)  Вы собираетесь положить в Банк 1000 долларов на 6 лет под 6% годовых. Какую сумму Вы получите в итоге если:

а)  Проценты рассчитываются каждый год;

б)  Проценты рассчитываются каждые полгода;

в)  Проценты рассчитываются каждый месяц;

2)  Вы собираетесь вкладывать по 100 долларов в банк каждый месяц в течении года под 6 % годовых. Сколько денег окажется на вашем счете, если:

а)  Вы вносите деньги в начале каждого месяца;

б)  Вы вносите деньги в конце каждого месяца;

3)  У вас есть 100 долларов. Под какую норму процента годовых Вы могли бы их инвестировать, чтобы получить через 3 года 200?

4)  По облигации номиналом в 1000 долларов предусмотрен следующий план начисления процентов течении 5 лет: 10 %, 15 %, 20 %, 25 %, 30 %. Рассчитайте будущую (наращенную) стоимость облигации через 5 лет.

5)  Измените ставку процента в задаче 4 за 1-й год таким образом, чтобы через 5 лет стоимость облигации составила 3000 долларов.

6)  Внесите данные, представленные в таблице 3.19

Таблица 3.19 – Исходные данные

Предположим, что фирма имеет возможность вложить деньги в 4 инвестиции, условия которых приведены в таблице. Вам необходимо следующее:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28