Главным при реализации данной концепции является соблюдение принципа полезности проводимой работы.

Социально-трудовая компетенция на наш взгляд является одной из самых важных, она предполагает овладение учеником знаниями и опытом в гражданско-общественной деятельности, в социально-трудовой сфере, в области семейных отношений и обязанностей, в вопросах экономики и права, а так же в профессиональном самоопределении. Т. е. данная компетенция подразумевает овладение детьми теми предметными знаниями, умениями и навыками, которые они будут использовать непосредственно в своей дальнейшей жизнедеятельности. Она может быть реализована следующим образом. Если постоянно развивать у детей способность применения умения вычислять в различных (в том числе и нестандартных) ситуациях, т. е. если постоянно проводить работу по усовершенствованию устного счёта у детей, то у них не возникнут проблемы такого плана, как вычислить сумму покупок в магазине до того момента как подойти к кассе, что относится к социально-трудовой сфере. Курс « Элементы статистики и теории вероятности» как обязательный компонент школьного образования, также необходим для социальной адаптации человека в динамично изменяющемся обществе для формирования функциональной грамотности.

Компетенция личностного самосовершенствования. Эта компетенция подразумевает овладение учеником теми способами деятельности, которые пригодятся ему в определённой современной жизненной ситуации. К ней относятся правила личной гигиены, забота о собственном здоровье, внутренняя культура, основы безопасности жизнедеятельности. Т. е. как и в случае с общекультурной компетенцией необходимо на подсознательном уровне сообщать ученику информацию, которая может потребоваться ему в его дальнейшей жизни. Математическое образование выступает здесь как средство самопознания, самовоспитания, саморазвития, самообразования. С целью реализации данной компетенции, можно внедрить такой вид деятельности на уроках математики, как решение задач с « лишними данными». Работа над такими задачами показала, что «лишние данные» не мешают ученикам при решении.

Предложенные разработки могут быть модернизированы, изменены или дополнены.

Всё зависит от уровня готовности учителя и учеников класса к реализации компетентностного подхода в своей учебной деятельности.

В заключение можно сделать вывод, что компетентностный подход можно и нужно реализовать на уроках математики. Для этого каждый учитель может разработать конкретные приёмы реализации ключевых компетенций на уроках математики. Поэтому возникает необходимость освоения педагогами новых педагогических технологий, позволяющих организовать деятельность учащихся на уроке с целью приобретения ими соответствующих компетентностей, планировать их развитие.

, учитель математики МОУ СОШ №36
ДЕЯТЕЛЬНЫЙ ПОДХОД В ОБУЧЕНИИ МАТЕМАТИКЕ.

Каким будет мир в середине XXI века, трудно себе представить не только школьным учителям, но и футурологам. Поэтому школа должна готовить своих учеников к переменам, развивая у них такие качества, как мобильность, динамизм, конструктивность. Смысл образования заключается в развитии у обучаемых способности самостоятельно решать проблемы в различных сферах и видах деятельности на основе использования социального опыта, элементом которого является и собственный опыт учащегося. С позиций компетентностного подхода уровень образованности определяется способностью решать проблемы различной сложности на основе имеющихся знаний, а система образования должна формировать (в условиях рыночной экономики) способность менять сферы и способы деятельности, выработать умения делать выбор, эффективно использовать ограниченные ресурсы, сопоставлять факты, вести переговоры, оперативно находить информацию.

Одной из целей школы является формирование ключевых компетенций, прежде всего учебно–познавательных, информационных и компетентностей личного самосовершенствования на протяжении жизни (классификация А. В. Хуторского-7 типов кл. комп.); выработка образовательных компетентностей таких как готовность и способность обучаться самостоятельно, самоконтроль, готовность решать сложные и спорные вопросы, принимать решения, нести персональную ответственность и др. (37 видов по Дж. Ревану).

В связи с обновлением содержания математического образования «организация управления обучением должна быть направлена не только на усвоение обучающимися определенной суммы знаний, но и на развитие личности, его познавательных и созидательных способностей» (Методическое письмо «О преподавании уч. предм. «Математика» в 2006—2007 уч. г. Одним из факторов, определяющих качество образования, является содержание предметных компетенций учителя. Кроме того, один из аспектов реализации компетентностного подхода предполагает определение целей, отбор содержания, организацию образовательного процесса, выбор образовательных технологий, оценку результатов. Психологические исследования (Л. В. Выгодский, А. Н. Леонтьев, П. Я. Гальперин) показали, что знания приобретаются лучше всего не с помощью совершенного изложения учителем материала, а в ходе работы ученика с этими знаниями.

Ученик должен учиться САМ, а учитель — осуществлять мотивационное управление его учением, т. е. мотивировать, организовывать, координировать, консультировать, контролировать.

Учитель при этом должен создать для учащихся возможность занимать активную позицию в учебном процессе, не просто «усваивать» предлагаемый учителем материал, а познавать мир, вступая с ним в активный диалог, самому искать ответы и не останавливаться на найденном как на окончательной истине. Ученик же должен «освоить управляющие функции учителя и обратить их на самого себя» (Д. Б. Эльконин), т. е. ученик должен стать одновременно и «я-учеником» и «я-учителем». Лишь в этом случае ученик будет в состоянии мотивировать свою деятельность, осуществлять её планирование и регуляцию, анализ и оценку.

Для организации деятельного подхода в обучении, увеличении самостоятельности учащихся в приобретении знаний, для достижения эффективности учебно-познавательной деятельности я в своей работе использую элементы таких современных образовательных технологий:

развивающее, проблемное, разноуровневое обучение, КСО, блочно-модульное обучение, игровые методы обучения, а в старших классах ещё и лекционно-семинарско-зачётная система обучения, обучение в сотрудничестве. Первые уроки учебного года, уроки повторения, начиная с 8 класса, я организую по структуре КСО (реши - объясни соседу по парте — обменяйся заданиями) работая с карточками разных тем предыдущего учебного года. На таких уроках работают все уч-ся, без принуждения продолжают работу дома, самостоятельно используя учебник и конспекты прошлого уч. года. В своей работе я стараюсь сочетать разные формы организации обучения: фронтальные, групповые, парные и индивидуальные, используя деятельный подход в обучении.

Во фронтальных работах применяю:

1.  фронтальные беседы с заранее запланированными вопросами по уровням развития учащихся.

2.  дидактические игры для сосредоточения внимания и заинтересованности учащихся («Учитель-класс», «Аукцион», «Кодированная проверка д/з», «Найди ошибку»).

3.  устное решение заданий по готовым карточкам и чертежам.

4.  создание проблемной ситуации и её анализ, формулировка проблемы с последующим её решением (экспериментально или теоретически).

В групповых и парных работах проявляется особенность каждого ученика, повышается их активность, смелее выясняются все непонятные вопросы, создаются комфортные условия для деятельности слабого ученика, даётся возможность продвижения в соответствии с учебными возможностями продвинутым учащимся, общения друг с другом на принципах самоуправления. Состав групп определяется дидактическими, психологическими и управленческими целями учителя (от 3 до 7 человек).

Формы групповых работ: дифференциально-групповая, звеньевая, кооперативно-групповая, бригадная. Различаются и способы «защиты» учебных заданий: устная форма («публичная защита», в которой представителя выставляет сама группа или назначает учитель); письменная форма с распределением оценок уравнительным методом или по коэффициенту трудового участия. Эти формы работ могут использоваться как на этапе изучения нового материала, на этапе закрепления изученного, так и на этапе контроля (зачёты). Не всегда важно справилась ли группа с заданием, важнее какие подходы использовала при работе, какой информацией пользовалась, как в этом участвовали все участники.

Полученные результаты могут оцениваться по трем параметрам: самооценка, оценка группы, оценка учителя. Д. Б. Эльконин утверждает, что рационально формировать учебную деятельность необходимо через формирование самоконтроля. Формы самоконтроля: итоговый, пооперационный, пошаговый (комментируя свои мысли вслух, объясняя свои действия), прогнозирующий. Обучаю учащихся таким приёмам формирования самоконтроля как: взаимоконтроль, взаиморецензирование, контроль за развёрнутым процессом решения каждой операции учебного задания на доске. Типы самоконтроля бывают по результату, по полноте состава и качеству действий. После того как произведён самоконтроль, можно установить, на сколько результаты соответствуют цели. Это уже процесс самооценки — критической позиции субъекта по отношению к себе. Совместно с учениками вырабатываются критерии самооценки по следующим уровням: «2»- уровень знаний - уровень представлений, ученик пассивен, только слушает, «3»- уровень знаний - вербальный, ученик уже проговаривает усвоенное, «4»- уровень знаний - уровень действий, ученик слушает, проговаривает и применяет усвоенное, «5»- уровень знаний - творческий, ученик предлагает новые способы действий.

Учитель математики находится под постоянным контролем разного уровня, причём требования к знаниям его учеников постоянно возрастают. Необходимой основой формирования умений и навыков учащихся в процессе обучения является система общих и специфических приёмов учебной деятельности — как умственной, так и практической. Владение совокупностью основных общеучебных умений и навыков и называют «умением учиться». Мною собрана папка с рекомендациями по организации учебного труда для учащихся — как «учиться математике», как заучивать учебный материал, как составлять план ответа, как вести тетради по математике, составлять конспекты, как осуществить взаимоконтроль и взаимопомощь в процессе выполнения задания, приемы самоконтроля и рецензирования, самостоятельная работа с учебником, как подготовить доклад, реферативно-исследовательскую работу, как использовать дополнительную литературу, организация домашней работы, приёмы работы над решением задач, примеров, приёмы усвоения теорем. Перечислю некоторые приёмы учебной деятельности, способствующие активизации учебного процесса, увеличению самостоятельности учащихся в приобретении знаний: приём «введите роль» — участие в управлении обучением (Фома неверующий, связник, подводящий итоги, спонсор знаний, почемучка, штурман, адвокат, психолог и др.), приём «дай себе помочь»- искусственное создание ситуации, в которой требуется помощь, помощь старшеклассников в проверке, в принятии зачётов, в разработке дидактических материалов; приём «Удивляй»-когда обыденное становится удивительным (пр. — изучение теоремы о сумме углов треугольника,7кл.); приём «Лови ошибку»- применим при всех формах работы; приём «Учебный Мозговой Штурм»- при работе в группах; приёмы опроса, повторения пройденного, подачи домашнего задания и др.

Для итогового контроля и оценки знаний, учащихся в своей работе я использую дифференцированные зачёты с такими активными формами как «математический ринг», групповые формы с участием старшеклассников в роли консультантов-экзаменаторов.

При реализации деятельностного подхода в обучении используются такие взаимоотношения как «учитель-группа-ученик». На подобных уроках нет скучающих учеников, свободное общение друг с другом и учителем, оказание взаимопомощи, ученики обучаются рациональному использованию времени, выбору задний по своим возможностям (самооценка), взаимопроверке и самопроверке. Взаимная информация и согласование, координация усилий, взаимное дополнение и обогащение, компенсация, взаимная опора и взаимопомощь, взаимосовершенствование — это элементы форм сотрудничества, обеспечивающие успешное развитие личности, её духовный рост в контексте компетентностного подхода, с учётом принципов соответствующих личностной парадигме образования. В результате компетентный педагог, владеющий компетенциями, включающими знания, умения, навыки, способы деятельности применяющий современные образовательные технологии способен обеспечить положительные и эффективные результаты в обучении, воспитании и развитии молодого поколения.

, учитель математики МОУ СОШ № 000
ФОРМИРОВАНИЕ У ОБУЧАЮЩИХСЯ УМЕНИЯ ПРИМЕНЯТЬ МАТЕМАТИЧЕСКИЕ ЗНАНИЯ И НАВЫКИ В НЕСТАНДАРТНЫХ СИТУАЦИЯХ.

Школа должна дать учащимся не только определенную сумму знаний, но и привить умение самостоятельно пополнять свой запас знаний, чтобы ориентироваться в стремительном потоке современной научно – технической информации» / Александров.

В условиях высокого уровня развития науки и техники особые требования предъявляются к подготовке учащихся в школе. Задача образования не может сводиться только к вооружению учащихся определённой суммой знаний. Необходимо сформировать у них умение оперировать приобретенными знаниями, применять их в новых ситуациях, делать самостоятельные выводы и обобщения, находить решения в нестандартных условиях.

Школа должна помочь ученику овладеть культурными (и выработанными им самим) способами деятельности, позволяющими ему действовать с ориентацией на позицию другого человека, социума, предметной области. Это означает, что в сферу интересов современного школьника помимо предметных знаний входят умение критически оценивать и находить пути решения возникающих проблем, анализировать ситуацию, адекватно владеть средствами коммуникаций, добывать информацию и пользоваться ею.

Собственное (практическое) действие школьника, когда он распознает проблемы, возникающие в окружающей действительности и, используя математические факты и методы, решает эту проблему, превращение всего богатства математики и других школьных предметов в материал для своего самоопределения, - это вопросы, требующие пристального внимания всех участников образовательного процесса в школе.

Отсутствие в методической системе обучения в целом направленности на формирование приемов учебной деятельности учащихся приводит ученика к неготовности к обучению, отсутствию самостоятельности, организационной и умственной беспомощности в учебной деятельности, в частности, на уроках математики. Данную ситуацию характеризуют результаты международных исследований (PISA, TIMSS) по оценке качества математического и естественнонаучного образования школьников России. В исследовании TIMSS-2003 российские восьмиклассники устойчиво превышали средние международные показатели по математике. Но за период годы исследование TIMSS выявило отрицательную тенденцию в состоянии математического образования школьников 8 класса (1995 г. – 38 %, 2003 г. – 30 % детей имели высокий и продвинутый уровни обученности по математике). Исследование PISA-2003 показало, что у пятнадцатилетних школьников России математическая грамотность ниже среднего мирового результата. Пятая часть учеников, принявших участие в исследовании, выполнили задание на уровне, при котором результаты не засчитываются, так как этот уровень по международным критериям не характеризует математическую грамотность; 11 % школьников не смогли применить свои математические знания даже в самых простых ситуациях, которые были предложены в исследовании и только 7 % имеют высокие уровни математической грамотности, которые проявляются в умении дать математическую интерпретацию относительно сложной незнакомой ситуации.

Причем приведенные данные характерны для ситуаций, когда вопросы относятся к разделам «Алгебра», «Геометрия» и «Числа». Намного хуже обстоят дела, когда школьникам необходимо использовать понятия и методы, связанные с вопросами «Вероятность», «Статистика», «Дискретная математика» и отнесенные мировой школьной системой образования к стандарту. Для российской школы изучение данных тем не входит в обязательную программу общеобразовательных школ.

Характерные тенденции – это неумение анализировать и интерпретировать количественную информацию, представленную в различной форме (таблиц, диаграмм, графиков реальных зависимостей) в средствах массовой информации; неумение применять собственный опыт или знания из других областей в ситуациях, приближенных к реальной жизни, недостаточное развитие пространственных геометрических и вероятностных представлений.

Чтобы повысить качество математического образования в школе, необходимо учить детей умениям выделять идеи и методы рассуждений, перестраивать из­вестные и находить новые при­емы учебной деятельности, выводить следствия, используя обобщенные связи между объектами и обоб­щенные приемы. Уделять как можно больше внимания вопросам решения прикладных задач, как в стандартных, так и в нестандартных ситуациях, самостоятельной работе школьников по использованию обобщенных приемов, справочников и других ресурсов. Ученик в школе, особенно в старших классах, должен овладеть умениями исследовательской работы средствами математики, в которой он использует различные источ­ники информации для само­образования.

В настоящее время практически весь курс школьной математики сводится к тренировке в выполнении определённых алгоритмов и к обучению детей решать типовые задачи, и посвящен выполнению ряда действий с построенной моделью: применение определенных теорем, преобразование выражений, решение уравнений, дополнительные построения на чертеже и т. д. А потому задача, которая стоит сейчас перед учителем математики – организация продуктивной деятельности учащихся по развитию качеств, относящихся к функциональной грамотности, формирование практико-ориентированных знаний и умений. Научить школьников думать, обосновывать и доказывать свои решения, не прибегать к механическому заучиванию материала, развивать способность, говорить «нет», когда все говорят «да», если понимаешь, что большинство не обязательно право, – эти умения необходимо развивать на уроках математики. Для этого необходимо включать в содержание уроков задания, направленные на развитие общеучебных умений и навыков, на выработку у учащихся умения применять математические знания и навыки в нестандартных ситуациях.

Необходимость развития у всех школьников вероятностной интуиции и статистического мышления становится насущной задачей обучения математике в основной школе. Именно вероятностно-статистическая линия, изучение которой невозможно без опоры на процессы, происходящие в окружающем мире, на реальный опыт школьника, способствует повышению математической грамотности в соответствии с мировыми стандартами.

Для адаптации традиционного содержания к целям новой содержательной линии «Элементы логики, комбинаторики, статистики и теории вероятностей» можно использовать следующие средства:

·  разнообразные задачи, способствующие формированию

·  комбинаторного мышления;

·  задания на сбор, систематизацию, наглядное представление и анализ данных, представленных в обозримых выборках;

·  беседы, во время которых фиксируется

внимание на случайных явлениях в быту, в природе и технике;

выделяются закономерности в случайных массовых явлениях.

Результаты исследований PISA, ЕГЭ и мониторинговых образовательных достижений школьников свидетельствуют о низком уровне сформированности умений работать с различными источниками информации. Успешное выполнение большинства заданий по математике связано с развитием такого важнейшего общеучебного умения, как умение внимательно прочитать некоторый связный текст, выделить в приведенной в нем информации только те факты и данные, которые необходимы для получения ответа на поставленный вопрос. Замечено, что «интересной воспринимается информация, в которой 35-40% знакомо, а остальное – ново» ().

Другую сторону вопроса составляет формирование у учащихся некоторых общих учебных умений. Для того чтобы самостоятельно изучать научную и техническую литературу, необходимы определённые навыки работы с текстом. Сюда относится умение читать текст, насыщенный информацией, вычленять из него главное, ставить перед собой вопросы и находить в тексте ответы на них, определять, что осталось не выясненным до конца, четко формулировать, что именно надо выяснить, обращаться за справкой к другому разделу книги или другой литературе и т. п. Вместе с тем, для того чтобы подготовить учащихся к применению знаний в конкретных условиях, к решению сложных вопросов, выбору из имеющегося набора решений оптимального варианта и т. д., необходимо сформировать определенные умения в решении задач. Их компонентами являются умения вычленять некоторые взаимосвязи, вытекающие из условия задачи, составлять план решения, осуществлять решение, привлекая в случае необходимости справочный материал, оценивать результат, проверять правильность решения.

Вот возможный вариант организации работы школьников с информацией при решении тестовых задач по математике.

На первых этапах школьник внимательно читает текст, при этом извлекает информацию из текста, и с помощью схем, рисунков, отрезков,… фиксирует существенное, то есть создает модель содержания задачи. Основное назначение этого этапа – научить школьников осмысленно читать текст задачи и фиксировать в сознании ту информацию, которая имеется в тексте задачи, при этом выявляя то математическое содержание, которое в него заложено. Как только большинство детей этим общеучебным навыком овладели, важно организовать переход к следующему этапу: фиксированию математического содержания каждого предложения с помощью числовых или буквенных выражений, которые впоследствии используются в ходе решения алгебраических и геометрических задач. Результатом такого фиксирования является составление школьником математической модели, с которой он выполняет ряд математических операций и затем обратно переводит на язык реальности.

В 8-9 классах при изучении или повторении тем: ромб, теорема Пифагора, площадь параллелограмма, подобные треугольники, приближенные вычисления можно предложить школьникам следующую нестандартную задачу.

Задача 1. ()

Инструкция по изготовлению воздушного змея

Для изготовления воздушного змея вам понадобятся четыре тонких деревянных рейки и кусок легкой, но прочной ткани. Сделайте каркас в форме ромба. Пропорции ромба можете изменить по своему желанию, но учтите, что чем больше площадь ромба, тем больше подъемная сила змея. Обтяните каркас тканью. Чтобы обеспечить достаточную прочность, кусок ткани должен быть цельным (его нельзя сшивать или склеивать из двух частей). Прибейте сверху ещё одну планку по диагонали: она будет держать ткань и придаст жёсткость вашей конструкции.

У ребят имеются несколько реек по 62 см длиной. Но у них возник спор о форме каркаса. Один предлагает сделать каркас квадратным, а другой считает, что это противоречит инструкции.

Задание1.

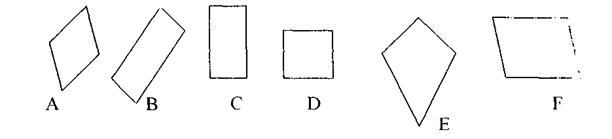
Обведите буквы под соответствующими фигурами кружком.

Придя в магазин за тканью, ребята увидели, что единственной подходящий материал имеет ширину всего 50 см. Один утверждает, что необходимо купить 62 см, другой – что необходимо гораздо больше. Продавец отмеряет только по 10 см.

Задание 2.

Сколько ткани нужно купить ребятам, чтобы обтянуть каркас для змея, если они собираются сделать его из целых реек, не распиливая их? (Чтобы не тратить лишних денег, они собираются купить необходимый минимум ткани.)

Задание 3.

Какой процент составит площадь получившегося змея от возможной максимальной площади при данной длине реек?

Оценка выполнения заданий

Данная задача содержит лишнюю информацию. Поэтому ученику следует многократно возвращаться к условию, чтобы извлечь нужную информацию. При работе с текстом необходимо объединить информацию, представленную в этих формах, и переформулировать её, используя математические понятия. Далее школьник проводит следующие операции:

·  сопоставляет геометрические понятия ромба и квадрата в коммуникативной ситуации; соотносит определение ромба с конкретными вариантами геометрических фигур;

·  моделирует: переводит словесное описание и объемное изображение в планиметрическую форму;

·  определяет необходимую степень точности вычислений, использует приближенные вычисления;

·  применяет приемы решения планиметрических задач (использование теоремы Пифагора) в нестандартной ситуации.

Наиболее частые ошибки в решении данной задачи могут быть связаны с тем, что опознание ромба основывается не на определении, а на чисто зрительной идентификации. Традиционно ромб изображают так, что одна его диагональ горизонтальна, а другая – вертикальна. Вследствие этого ученики могут воспринять фигуру «Е» за ромб. А ромбы «D» и «F» могут не быть опознаны. Поэтому необходимо побудить школьников последовательно соотнести каждую фигуру с определением ромба. При определении количества материи для каркаса школьники могут округлить число по правилу округления, которое они изучают в курсе математики, и совершенно не соотнести со смыслом задачи, с жизненной ситуацией. При наличии ошибки следует привлечь ученика к тщательному анализу содержания задачи, чтобы он осмысленно прочитал тест и извлек нужную информацию, так как без овладения этого умения школьник не решит задачу.

Таким образом, не отказываясь от традиций и достоинств школьного математического образования необходимо органично ввести в образовательный процесс новые приоритеты, целенаправленно обучая школьников умениям применять математические знания для решения реальных проблемных ситуаций, связанных с разнообразными аспектами окружающей жизни.

Литература

1.  Концепция модернизации российского образования на период до 2010 года.

2.  Исследования PISA_TIMSS_2003. Исследования PISA-2003.

3.  Задания для проверки математической грамотности. // Исследования PISA-2003. Приложение 2, стр. 66-72.

4.  Математика. //Материалы для учителя. PISA -2000.- М., 2003

5.  Епишева обучения математике на основе деятельностного подхода. – М.: Просвещение, 2003.

6.  Ким подходы и практические методы модернизации математического образования в основной и старшей школе. - Хабаровск, ХК ИППК ПК, 2004.

7.  , Крашенинникова гуманизации образования. Дифференциация при обучении математике. - Хабаровск, 2005.

8.  Семенко курсы разных направлений.- Математика в школе. №стр.45-52.

9.  Бунимович и статистика, 5-9 кл. – М.: Дрофа, 2002

10. Бунимович -статистическая линия в базовом школьном курсе математики. – Математика в школе, № 4, 2002.

11. , Суворова указания к теме «Статистические исследования». – Математика в школе, № 3, 2003.

12. О подготовке учителей к обучению школьников к стохастике. – Математика в школе, № 4, 2003.

13. и др. Элементы стохастики в курсе математики 7-9 классов основной школы. – Математика в школе, № 3, 2003.

14. Ткачева данных в учебниках и других. – Математика в школе, № 5, 2003.

15. , Смирнова . Экзамен для всех. Система заданий для контроля. - М. ИЦ «Вентана-Граф», 2005 г.

информатики МОУ лицея № 97
ЭСТЕТИЧЕСКОЕ ВОСПИТАНИЕ УЧАЩИХСЯ НА УРОКАХ МАТЕМАТИКИ.

К. Д. Ушинский уделял серьезное внимание воспитанию у ребенка эстетического чувства, подчеркивая значение для этой цели художественной литературы, музыки, изобразительного искусства и особенно природы. «Странно, что воспитательное влияние природы, которое каждый более или менее испытал на себе, так мало оценено в педагогике». Ушинский стремился воспитывать в детях способность чувствовать, переживать, наслаждаться прекрасным. «Во всякой науке, — замечал он, — более или менее есть эстетический элемент, передачу которого ученикам должен иметь в виду наставник. Не только содержание, но и форма обучения и воспитания должна развивать чувство любви к прекрасному».

Возможность ощущать в одно время целое и малейшие его подробности, по Ушинскому, есть чувственная основа возможности наслаждения гармонией созданий природы и художества.

Естественные науки немало способствуют развитию всех духовных способностей. Сближая человека с природой, они наполняют его воображение бесконечно разнообразными впечатлениями и формами; на каждом шагу представляя бесчисленные задачи, возбуждая внимание и любознательность; представляя самые сложные и запутанные отношения явлений, изощряют силу анализа, давая ежеминутно чувствовать неприложный закон, дают мысли движение к высшим теоретическим и философским обобщениям.

Ушинский писал, что каждая наука развивает человека настолько, «насколько хватает ее собственного содержания». Развитию гармоничной личности способствуют не только литература, изобразительное искусство, музыка, естественные науки, но и математика.

Математика обладает «красивым» содержанием, которое точно описывает окружающую человека действительность, да и самого человека. В связи с этим необходимо вспомнить о том, что самые красивые произведения искусства: живопись, скульптура, графика, музыка, поэзия в своей основе имеют математическое обоснование.

Художники эпохи Возрождения всерьез занимались основами проективной геометрии, т. к. отражение объективной реальности на плоском холсте требовало знания законов, по которым любое изображение становилось объемным. Вписав человеческое тело в окружность, Леонардо да Винчи подтвердил существование гармонии между природой и математическим началом.

Человеческие тела и лица изображались с учетом пропорции золотого сечения. Именно на пересечении линий золотого сечения художники изображали наиболее важные фрагменты, которые хотели отметить особо. Сам да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».

В основе любого поэтического шедевра лежит закономерность сочетания слогов, последовательности ударений, пауз, то есть стихотворный размер. А. С. Пушкин отдавал предпочтение двусложным размерам – ямбу (V–), хорею (–V), которые несут простоту, ясность, логичность в выражении чувств.

Философские рассуждения, грусть, печаль и т. д. передавали с помощью трехсложных размеров: дактиля (–VV), амфибрахия (V–V), анапеста (VV–). Примером могут быть произведения М. Ю. Лермонтова, Н. А. Некрасова.

Любая задача или теорема имеют несколько способов решения или доказательства. Под красивыми понимаются те из них, которые выполнены наиболее рациональным (целесообразным) способом. Чем меньше делается ссылок на дополнительный материал, тем «стройнее» решение или доказательство (конечно, не в ущерб содержанию и истинности). Красивое решение – доступное решение.

При доказательстве теоремы стереометрии о перпендикулярности прямой к плоскости наиболее короткий путь предоставляет векторный метод.

В некоторых планиметрических задачах наиболее выигрышно применение метода координат, незаслуженно игнорируемого на практике.

В преподавании математики особую роль играют образцы решений, которые служат для воспитания аккуратности, эстетического вкуса. Учащихся необходимо информировать о том, что в критерий оценки входит качество оформления, которое распространяется на чертежи, описание.

, учитель математики МОУ лицея № 97
РАЗВИТИЕ ТВОРЧЕСКИХ КОМПЕТЕНЦИЙ ЧЕРЕЗ ОРГАНИЗАЦИЮ ПРОЕКТНОЙ ДЕЯТЕЛЬНОСТИ УЧАЩИХСЯ.

Общество информационных технологий или как его называют постиндустриальное общество в отличие от индустриального общества конца XIX — середины ХХ века гораздо в большей степени заинтересовано в том, чтобы его граждане были способны самостоятельно, активно действовать, принимать решения, гибко адаптироваться к изменяющимся условиям жизни.

Отсюда современное информационное общество ставит перед всеми типами учебных заведений и прежде всего перед школой задачу подготовки выпускников, способных:

·  гибко адаптироваться в меняющихся жизненных ситуациях, самостоятельно приобретая необходимые знания, умело применяя их на практике для решения разнообразных возникающих проблем, чтобы на протяжении всей жизни иметь возможность найти в ней свое место;

·  самостоятельно критически мыслить, уметь увидеть возникающие в реальной действительности проблемы и искать пути рационального их решения, используя современные технологии; четко осознавать где и каким образом приобретаемые ими знания могут быть применены в окружающей их действительности; быть способными генерировать новые идеи, творчески мыслить;

·  грамотно работать с информацией (уметь собирать необходимые для решения определенной проблемы факты, анализировать их, выдвигать гипотезы решения проблем, делать необходимые обобщения, сопоставления с аналогичными или альтернативными вариантами решения, устанавливать статистические закономерности, делать аргументированные выводы, применять полученные выводы для выявления и решения новых проблем);

·  быть коммуникабельными, контактными в различных социальных группах, уметь работать сообща в различных областях, в различных ситуациях, предотвращая или умело выходя из любых конфликтных ситуаций;

·  самостоятельно работать над развитием собственной нравственности, интеллекта, культурного уровня.

Среди разнообразных направлений новых педагогических технологий наиболее подходящими поставленным целям является:

·  метод проектов;

·  индивидуальный и дифференцированный подход к обучению.

Метод проектов всегда ориентирован на самостоятельную деятельность учащихся — индивидуальную, парную, групповую, которую учащиеся выполняют в течение определенного отрезка времени. Метод проектов всегда предполагает решение какой-то проблемы, предусматривающей, с одной стороны, использование разнообразных методов, средств обучения, а с другой, интегрирование знаний, умений из различных областей науки, техники, технологии, творческих областей. Результаты выполненных проектов должны быть, что называется, «осязаемыми», т. е., если это теоретическая проблема, то конкретное ее решение, если практическая, конкретный результат, готовый к внедрению.

Основные требования к использованию метода проектов.

1.  Наличие значимой в исследовательском, творческом плане проблемы/задачи, требующей интегрированного знания, исследовательского поиска для ее решения.

2.  Практическая, теоретическая, познавательная значимость предполагаемых результатов.

3.  Самостоятельная (индивидуальная, парная, групповая) деятельность учащихся.

4.  Структурирование содержательной части проекта (с указанием поэтапных результатов).

5.  Использование исследовательских методов: определение проблемы, вытекающих из нее задач исследования, выдвижение гипотезы их решения, обсуждение методов исследования, оформление конечных результатов, анализ полученных данных, подведение итогов, корректировка, выводы.

От учащихся требуется:

·  знание и владение основными исследовательскими методами (анализ литературы, поиск источников информации, сбор и обработка данных, научное объяснение полученных результатов, видение и выдвижение новых проблем, выдвижение гипотез, методов их решения);

·  владение компьютерной грамотностью, что предполагает:

§  умение вводить и редактировать информацию (текстовую, графическую), пользоваться компьютерной телекоммуникационной технологией, обрабатывать получаемые количественные данные с помощью программ электронных таблиц, пользование базами данных, распечатку информации на принтере;

§  владение коммуникативными навыками;

§  умение самостоятельно интегрировать ранее полученные знания по разным учебным предметам для решения познавательных задач, содержащихся в телекоммуникационном проекте.

Проекты могут быть:

·  исследовательские

·  творческие

·  приключенческие, игровые

·  информационные проекты

·  практико-ориентированные

По характеру проекты могут быть:

·  с открытой, явной координацией

·  со скрытой координацией

Если это исследовательский проект, то он с неизбежностью включает этапность проведения, причем успех всего проекта во многом зависит от правильно организованной работы на отдельных этапах. Поэтому необходимо отслеживать такую деятельность учащихся поэтапно, оценивая ее шаг за шагом. При этом и здесь, как и при обучении в сотрудничестве оценка необязательно должна выражаться в виде отметок. Это могут быть самые разнообразные формы поощрения вплоть до самого обычного. В творческих проектах часто бывает невозможно оценить промежуточные результаты. Но отслеживать работу все равно необходимо, чтобы вовремя придти на помощь, если такая помощь потребуется (но не в виде готового решения, а в виде совета). Другими словами, внешняя оценка проекта (как промежуточная, так и итоговая) необходима, но она принимает различные формы в зависимости от множества факторов. Учитель проводит постоянный мониторинг совместной деятельности, но не навязчиво, а тактично в случае необходимости приходя на  помощь.

В частности, по математике в прошлом году мы с учащимися 11 класса работали над следующими темами: « Математические модели экономического роста», «Задачи линейного программирования» и «Взгляд на мир сквозь призму симметрии».

Так как все эти темы не входят в школьный курс математики, то вначале в 10 классе мне пришлось рассказать в полном объеме темы: Интегралы. Дифференциальные уравнения с разделяющимися переменными. Задачи линейного программирования. А затем, девочки, с которыми мы работали, выбрали те направления, которые им больше понравились и были более понятными. Все работы оказались связанными с приложениями математики: в экономику, в маркетинг и в культурологию, так как работа о Симметрии затронула не только математический взгляд на симметрию, но и мышление (оно тоже может быть симметричным), дизайн, архитектуру, живопись. Дети приготовили интересные презентации в приложение к работам.

.  Важно помнить, что проект — это решение, исследование определенной проблемы, ее практическая или теоретическая реализация. Этим метод проекта отличается от работы над темой, где часто достаточно просто усвоить новый материал по теме; от ролевой игры, дискусии, пр., где роли распределяются в групповой работе для осуществления методического замысла: лучшего усвоения материала, стимулирования интереса, мотивации познавательной деятельности учащихся. Все указанные методические цели могут присутствовать и при использовании метода проектов, но, кроме всего прочего, ему обязательно присуще исследование проблемы, творческая, поисковая деятельность, находящая воплощение в каком-то конкретном продукте.

, учитель математики МОУ гимназия № 23
ПОДГОТОВКА УЧАЩИХСЯ 9-Х КЛАССОВ К ЭКЗАМЕНУ В УСЛОВИЯХ ЭКСПЕРИМЕНТА.

Основная подготовка выпускников 9-х классов к единому государственному экзамену осуществляется в течение всего периода их обучения в школе. Однако нельзя отрицать, что от целенаправленной подготовки учеников к этому экзамену на завершающей стадии их обучения зависит очень многое.

Рассмотрим несколько аксиом подготовки учащихся к экзамену:

1.  Не следует сводить подготовку учащихся к натаскиванию на определенный список типов задач, каким бы он не был обширным. Требуется совместить подготовку учащихся к экзамену с проведением работы по их развитию в интеллектуальной, мотивационной, эмоциональной, предметно-практической сферах личности.

2.  Следует знакомить, отрабатывать, повторять методы решения задач. Каждый из общих методов решения задач должен быть методически обработан и для каждого из них разработаны педагогические средства для работы с учащимися.

3.  Состав методических средств по общим методам решения задач включает:

·  Общая идея метода

·  Решение примеров

·  Способы самоконтроля

·  Прогноз на изменения усложнения заданий

·  Систематизация материалов

·  Мониторинг подготовки учащихся к реализации метода

4.  Требуется уделять особое внимание систематизации методов решения задач.

Методические принципы подготовки учащихся к сдаче экзамена в условиях эксперимента заключается в следующем:

1.  Принцип сотрудничества: ученик может быть инициатором того, что будет рассматриваться в тот или иной период подготовки.

2.  Принцип регулярности. Работа по подготовке к сдаче экзамена должна проводиться постоянно. Для этого следует включать задания как для работы в классе, так и в домашнюю работу. Следует создать такую атмосферу в классе, чтобы ученики самостоятельно занимались не только теми заданиями, которые предлагает учитель, но и старались искать задания, выбираемые по собственной инициативе.

3.  Принцип параллельности. При подготовке к экзамену следует иметь в виду не только последовательную работу с заданиями по отдельным темам математики, но и комплексные задания на все темы школьной программы, изученные к этому времени и все методы решения задач. Этим самым прекращается процесс забывания и практически весь материал постоянно в работе. Такой подход обеспечивает постепенное углубление и рост возможностей школьников выполнять задания.

4.  Принцип оптимальной сложности. Уровень сложности не должен быть сильно завышен и должен быть адекватен сложностям заданий, которые уже предлагались.

5.  Важно уделять особое внимание обучению распознавания идей и методов решения.

6.  Важно, чтобы школьники осознали – красивые и правильные идеи ничто, если не будет правильного ответа.

7.  Важно при минимальном числе задач показать разнообразные методы решения задач.

8.  Принцип ориентации на развитие школьников. Не следует сводить подготовку учащихся к натаскиванию на определенные типы задач, встречавшиеся ранее. Необходимо, используя заинтересованность школьников в подготовке к экзамену, совместить её с проведением работы по развитию школьников.

В 9-х классах ученикам очень тяжело ориентироваться в большом объёме вопросов, охватывающих весь материал школьной программы. Иногда они просто не понимают смысла заданного вопроса или теряются в их количестве, т. к. вопросы рассматриваются из разных разделов алгебры.

В своей практике я применяю метод «пяти минут». На каждом уроке учащимся предлагается в течение 5—7 минут выполнить от 5 до 10 заданий по различным темам математики. Причем некоторые из заданий учащиеся могут сделать устно. Результат проверяется сразу же и обсуждаются те номера, которые вызвали затруднения у учеников. Такие листы помогают учащимся систематизировать весь учебный материал и помогают ликвидировать пробелы в знаниях.

, учитель математики МОУ гимназия № 23
ПРИМЕНЕНИЕ КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ НА УРОКАХ МАТЕМАТИКИ.

В одобренной Правительством России Концепции модернизации российского образования на период до 2010 года используется понятие «компетентность», и система универсальных знаний, умений, навыков, а также опыт самостоятельной деятельности и личной ответственности названы «современными ключевыми компетенциями». Таким образом, альтернативой доминировавшей долгие годы предметно-знаниевой модели обучения и воспитания становится модель компетентностного подхода.

Сама компетентность рассматривается как «способность к решению задач и готовность к своей профессиональной роли в той или иной области деятельности». Соответственно, компетенция предъявляется, в первую очередь, работодателями и обществом в виде некоторых специфических ожиданий, связанных с профессиональной деятельностью выпускника.

Вполне очевидно, что современная экономика ориентирована на кадры, которые владеют не разрозненными знаниями и умениями, а обобщенными, проявляющимися в умении решать жизненные и профессиональные проблемы.

Революция в информационно-коммуникационных технологиях, становление глобального рынка труда диктуют новые требования ко всем уровням образования – от школьного до профессионального.

Обучение в школе должно обеспечить формирование у детей новых компетентностей, знаний и умений, способов деятельности, которые им потребуются в новой информационной среде обитания, в том числе и для получения образования в условиях широкого использования современных информационных технологий обучения. Применение этих технологий в обучении математике объясняется также необходимостью решения проблемы поиска путей и средств активизации познавательного интереса учащихся, развития их творческих способностей, стимуляции умственной деятельности.

Круг методических и педагогических задач, которые можно решить с помощью компьютера, разнообразен. Компьютер – универсальное средство, его можно применить в качестве калькулятора, тренажёра, средства контроля и оценки знаний и средств моделирования, к тому же это — идеальная электронная доска. Важной методической задачей, в плане применения компьютера, является обучение решению задач, а так же некоторым основным способам математических действий, алгоритмам.

Дидактические функции компьютера в преподавании математики:

1.  Выполнение упражнений, когда учащимся предлагаются ранжированные по трудности задания.

2.  Электронная доска, использование мультимедиа – проектора на уроках математики.

3.  Моделирование.

4.  Исследование, когда из числа предлагаемых вариантов ученик выбирает, аргументируя, собственное решение.

5.  Математические расчеты в курсах других дисциплин.

Обучающие компьютерные программы реализуют одно из наиболее перспективных применений новых информационных технологий в преподавании и изучении математики. Они позволяют давать иллюстрации важнейших понятий курса математики на уровне, обеспечивающем качественные преимущества по сравнению с традиционными методами изучения. В их основе заложено существенное повышение наглядности, активизации познавательной деятельности ученика, сочетания механизмов вербально – логического и образного мышления. Применять компьютерные программы можно на любом этапе учебной деятельности: при изучении нового материала, закреплении, на обобщающих уроках и при повторении. Задача учителя – правильно организовать эту работу.

При изучении математики эффективны уроки-презентации. Такие уроки эстетически привлекательны, на них реализуются принципы доступности, наглядности. Урок-презентация также обеспечивает большой объем информации и заданий за короткий период. Всегда можно вернуться к предыдущему слайду (обычная школьная доска не может вместить тот объем, который можно поставить на слайд).

Таким образом, использование компьютерных технологий на уроках математики позволяет реализовывать следующие цели процесса обучения: повысить качества знаний по теме, продолжить формирование информационной культуры, наиболее полно реализовать учебные возможности каждого ученика.

, учитель математики МОУ СОШ № 000
КОМПЕТЕНТНОСТНЫЙ ПОДХОД В ОБУЧЕНИИ МАТЕМАТИКЕ.

Из перспективных направлений современного образования наиболее значимым является компететностный подход.

В последнее время в педагогических исследованиях стал широко применяться компетентностный подход. В соответствии с этим подходом при рассмотрении профессиональной подготовки учителей математики необходимо исходить из современного понимания профессиональной компетентности учителя, его профессионального мастерства.

В педагогической науке понятие «профессиональная компетентность педагога» рассматривается по-разному в зависимости от контекста решаемых исследовательских научных задач.

Выделяются составляющие компетенций, виды компетенций для учителей математики и для учащихся.

Использование проектной и информационно – коммуникационных технологий дает хорошие результаты при формировании у учащихся следующих компетенций:

·  «Самостоятельная познавательная деятельность, основанная на усвоении способов приобретения математических знаний из различных источников информации»;

·  «Математическая грамотность».

Развитию данных компетенций у учащихся способствует подготовка проектов. Для организации проектной деятельности может быть обозначена единая тема. Для подготовки проектов на внутришкольном уровне целесообразно сформировать группы (команды) участников. Ими могут быть ученики основной, средней школы.

В рамках единой темы каждая из команд участников выделяет собственную проблему, решению которой и посвящает свой проект.

В проектах возможно выделение проблем, связанных с использованием информационных технологий, учебного оборудования.

Требования к проекту

Для того, чтобы проект отвечал задачам развития и оценки самостоятельной познавательной деятельности, основанной на усвоении способов приобретения математических знаний из различных источников информации и математической грамотности учащихся, в нем должно быть следующее:

1. Выделены темы, которые будут освещены школьниками.

2. Выделены проблемы, которые могут быть решены при участии школьников.

3. Обоснованы способы и условия решения проблем, их реалистичность.

4. Определены возможные следствия предлагаемых проектных решений, возможные риски.

5. Сформулированы обобщающие выводы.

6. Желательно, чтобы проект основывался на определенной исследовательской базе.

7. Для оценки проектов целесообразно сформировать жюри из администрации школы, учителей математики, учащихся.

8. Проекты могут быть оценены с использованием листа экспертной оценки.

Учащимися 101 класса МОУ СОШ № 000 в уч. году разрабатывется проект «Тригонометрические уравнения и неравенства».

СЕКЦИЯ № 9
«Формирование и развитие ключевых и специальных компетенций учащихся средствами физики»

Паршакова Ю. В., учитель физики МОУ СОШ № 151
ПРЕДСТАВЛЕНИЕ ЭЛЕКТРОННОЙ МОДЕЛИ СОДЕРЖАНИЯ ШКОЛЬНОГО ОБРАЗОВАНИЯ НА ОСНОВА КОМПЕТЕНТНОСТНОГО ПОДХОДА.

Электронная модель содержания школьного образования по физике включает в себя представленный с помощью особой технологии Государственный образовательный стандарт. Работа по созданию модели начинается с осмысления образовательного стандарта.

Содержание образовательного стандарта по физике нормируется путем задания: целей его изучения; обязательного минимума содержания; требований к подготовке выпускников.

Т. о. образовательный стандарт по физике определяет лишь перечень элементов содержания, что не позволяет ответить на такие вопросы:

·  Как обеспечить проектирование содержания образования на уровень школы?

·  Как построить учебный процесс, нормализовав нагрузку учащихся?

·  Какова глубина изучения учебного материала и соответственно, какова сложность контрольных заданий при организации мониторинга реализации требований стандарта?

·  Как обеспечить формирование компетенций?

В представлении содержания образования по физике можно выделить такие блоки как:

— взаимосвязанные дидактические единицы; взаимосвязанные цели обучения, соответствующие требованиям «знать, понимать т. п.», которые обеспечиваются определенными дидактическими единицами; предметные компетенции, формирование, которых обеспечивается через достижение каких-либо целей обучения.

Этапы построения модели стандарта представлены нами в виде таблиц – на основе таксономии Бенджамина Блума.

Таблица 1 Дидактические единицы обязательного минимума содержания основных образовательных программ по физике — на данном этапе работы, после занесения в таблицу дидактических единиц, выявляются их взаимосвязи и заносятся в таблицу номера входящих и выходящих ДЕ.

Таблица 2. Требования к уровню подготовки выпускников (таксономия Б. Блума целей обучения) — устанавливаем ДЕ, обеспечивающие цели обучения, указывая их в соответствующей графе, одновременно заполняя последнюю графу первой таблицы. Выявляем связи, между целями обучения занося их в соответствующие графы, указываем компетенции, формирование которых обеспечивается через достижение данной цели. Определяем категорию Б. Блума для каждой цели обучения.

Таблица 3. Требования к уровню подготовки выпускников (компетенции) — представление предметных компетенций и целей обучения, обеспечивающих формирование данных предметных компетенций.

Для того, чтобы определить достигнута та или иная цель, или нет необходим инструментарий оценивания, который также представлен в виде отдельной таблицы.

Т. о. набор таблиц по предмету и является инструментально прописанной целью. Такая работа позволяет устранить нестыковки между темами, увидеть в целом все содержание учебного предмета, общие цели изучения предмета образования, место и роль каждой темы в достижении этих целей.

Зачем это нужно?

1.  концентрация усилий на главном (упорядочивание целей, определяя первоочередные задачи, порядок и перспективы работы);

2.  ясность работы: конкретные учебные цели дают возможность разъяснять ученикам ориентиры в их учебной работе

3.  создание эталонов оценки результатов обучения.

Данная модель содержания образования по физике представлена нами в календарно-тематическом планировании.

Большим подспорьем в работе учителя физики выступают электронные учебники по физики 8—11 класс. Учебники содержат в себе теоретическую и практическую часть. Последняя представлена системой мониторинга знаний, что позволяет учителю четко проследить за формированием предметных компетенций. Содержание учебников тесно связано с содержанием Государственного образовательного стандарта по физике, что позволяет нормировать содержание образования и вести четкий учет степени понимания материала (уровни – знание, понимание, применение).

, учитель физики МОУ СОШ № 124
ОЦЕНКА КАЧЕСТВА УСВОЕНИЯ ЗНАНИЙ И УМЕНИЙ УЧАЩИХСЯ ПРОФИЛЬНОЙ ШКОЛЫ В УСЛОВИЯХ ДИФФЕРЕНЦИАЦИИ И ИНДИВИДУАЛИЗАЦИИ ОБУЧЕНИЯ.

Стратегия модернизации образования, декларируемая «Концепцией модернизации российского образования на период до 2010 года», предполагает, в частности, его индивидуализацию и дифференциацию.

Дифференциация обучения (дифференцированный подход в обучении) – это: 1) создание разнообразных условий обучения для различных школ, классов, групп с целью учета особенностей их контингента; 2) комплекс методических, психолого-педагогических и организационно-управленческих мероприятий, обеспечивающих обучение в гомогенных группах.

Индивидуализация обучения предполагает частичное, временное изменение ближайших задач и отдельных сторон содержания учебно-воспитательной работы, постоянное варьирование ее методов и организационных форм с учетом общего и особенного в личности каждого ученика для обеспечения всестороннего ее развития.

На государственном уровне дифференциация и индивидуализация образования осуществляется путем введения профильного обучения на старшей ступени общего образования. Согласно «Концепции профильного обучения» содержание профильного обучения должно предусматривать значительную дифференциацию обучения и возможность построения школьниками индивидуальной образовательной программы.

Теоретическими предпосылками осуществления дифференциации и индивидуализации обучения в старшей профильной школе являются, на наш взгляд, личностно ориентированный, мотивационный и компетентностный подходы.

Под компетентностью в психолого-педагогической литературе понимают сложное интегративное качество личности, обуславливающее готовность осуществлять некоторую деятельность. Компетентность, как свойство индивида существует в различных формах: в качестве степени умелости, способа личностной самореализации (привычка, способ жизнедеятельности, увлечение), некоего итога саморазвития индивида или формы проявления способности и др.

Совокупность компетентностей выпускников школы следует рассматривать как результаты образования.

Проблема повышения качества результатов образования является одной из наиболее актуальных проблем, для решения которой в настоящее время на государственном уровне осуществляется становление общенациональной системы контроля качества образования. Главными направлениями этой системы являются стандартизация образования и введение института ЕГЭ, то есть производится технологизация образовательного процесса.

Одним из обязательных компонентов образовательного процесса является контроль и оценка качества усвоения учащимися знаний, умений и навыков. Обязательность этого компонента диктуется моделью цикла управления вообще и управления процессом обучения в частности, поскольку контроль осуществляет обратную связь в процессе обучения.

Применяемая ныне пятибалльная система оценивания знаний, умений и навыков учащихся удобна только при таком подходе к обучению, который не учитывает личностные особенности детей, их индивидуальные успехи. Учителя очень часто оказываются в тупике, используя пятибалльную систему при оценке творческих, научных работ школьников. Отдав в некоторых случаях им самый высокий балл, они определяют большую часть класса в троечники.

Кроме того, в последнее время произошло сужение пятибалльной системы оценок до четырехбалльной, нередко до трехбалльной, поэтому наблюдается формализм в оценке многоуровневых заданий. Учитель в настоящее время вынужден разную степень обученности оценивать одним и тем же баллом. В создавшейся ситуации учителю недостаточно трехбалльной системы, поэтому он сам расширяет ее, используя отметки со значками «плюс» и «минус». Все это снижает достоверность и надежность пятибалльной шкалы оценок как инструмента измерения степени обученности, соответствующей уровневой структуре знаний, требованиям образовательного стандарта.

В связи с вышесказанным возникает необходимость совершенствования системы педагогического контроля, одним из направлений которого является разработка новых технологий оценки качества учебных достижений школьников.

В большинстве работ, посвященных решению данной проблемы, предлагается использовать многобалльной оценочной шкалы.

Примерами технологии оценки качества учебных достижений школьников на основе многобалльной шкалы оценки могут служить:

·  12-балльная шкала оценок, предложенная В. П. Беспалько;

·  10-балльная шкала оценок, предложенная И. С. Карасовой;

·  10-балльная шкала оценок, применяемая в школах Латвии;

·  100-балльная шкала оценок, описанная Ю. Н. Малиевым.

Нами разработана технология разноуровневой оценки знаний и умений учащихся на основе многобалльной оценочной шкалы. Основу данной технологии составляет матрица 100-балльной шкалы оценки для трех уровней обучения школьников (базовый, профильный, уровень углубленного изучения) и трех уровней их достижений (репродуктивный, конструктивный, продуктивный). Дидактический материал этой технологии составляют контрольно-оценочные задания. Система коррекции полученных результатов образовательного процесса до запланированных основана на индивидуальном подходе, а ее содержание составляют индивидуальные недельные домашние задания, позволяющие ученикам устранить пробелы в своих знаниях.

Внедрение данной технологии в образовательный процесс позволило повысить качество усвоения учащимися знаний и умений по физике и уровень их мотивации учения по физике; способствовало позитивному изменению эмоционального и познавательного отношения учащихся к учебному предмету «физика».

, учитель физики и математики МСКОУ школа-интернат № 11
ФОРМИРОВАНИЕ И РАЗВИТИЕ ИНФОРМАЦИОННОЙ КОМПЕТЕНТНОСТИ У УЧАЩИХСЯ С ТНР НА УРОКАХ ФИЗИКИ.

Подготовка к работе с информацией.

Процедуре работы с информацией (выделение существенных элементов, конспектирование и реферирование, преобразование информации из одной формы в другую и так далее) можно учить в любой предметной области. Легче всего построить такие задачи для гуманитарных дисциплин.

Приведем несколько примеров.

1. Использовалась при организации самостоятельной работы с учебником по теме «Механическое движение», учебник , 2005 г.

Прочтите текст параграфа.

A) Какие слова встречаются в тексте наиболее часто? Сколько раз
попадается каждое из них? (Выпишите эти слова на листочке).

Б) Какие слова выделены в тексте жирным шрифтом? Почему? Какую особенность в проявлении этих слов вы заметили?

Выделены слова: относительно, механическое движение, траектория, путь, перемещение. Это новые слова. Перед ними везде стоит слово называют. Учитель подчеркивает, что слово называют и его варианта (называется и так далее) являются сигналами о появлении новых слов, которые следуют запомнить и понять, что они означают. В последующем будим говорить о понятиях, терминах и определениях.

B) Слова, которые часто встречаются, при записи текста для себя можно сокращать. Сокращение должны быть понятными и удобными. Как бы вы сократили слова из задания А?

В ходе беседы с учениками согласились, что сокращать короткое слово путь нет необходимости. Слова: относительно, механическое движение, траектория, перемещение можно и нужно сокращать (записывают на доке получившиеся сокращения).

Г) Какое предложение выделено в тексте жирным шрифтом? Почему? Выделено предложение, например, «Длина траектории, по которой движется тело в течении некоторого промежутка времени, называется путем». В последующем такие предложения мы будем называть определениями.

Д) Учитель обращается к конкретному ученику: «Если бы ты читал этот пункт учебника вслух для товарища, как бы ты дал им понять, что это предложение главное? Попробуй!»

При всех вариантах ответа появляется мысль о выделении нужной фразы голосом (интонацией). При выполнении этого упражнения происходит ещё и ненавязчивое, так как присутствует элемент игры, но надёжное заучивание определения. (А при работе с детьми с тяжелым нарушением речи такая работа очень важна.)

2. Использовалась при изучении темы «Единицы длины». Сейчас я произнесу несколько раз одно и то же предложение. Попробуйте уловить разницу. Как при этом меняется смысловой оттенок - что именно становить каждый раз главным?

Учитель произносить пять раз предложение, «за основную единицу длины принят метр», делая последовательно логическое ударение на всех словах, кроме предлога. Ученики ищут различия и со свойственным им «языковым чутьём» находят их, хотя часто затрудняются в том, чтобы правильно и понятно сформулировать свои мысли.

A) Основную: здесь выделено, что есть и другие единицы длины, но
метр среди них играет главную роль - через него выражаются все остальные.

Б) Единицу: подчеркнута особая роль метра - именно тот факт, что через него выражаются все длины, все с ним сопоставляются.

B) Длины: акцентировано, что метр является единицей именно этой
величины - длины, а для других величин имеются другие единицы.

Г) Принят: указывается на относительность измерения - единицей могло стать что-то другое. Так исторически и было. Учитель может потратить несколько минут на рассказ об истории измерений единиц длины, мерах длины у разных народов и в разные времена. Не будет лишним и рассказ об эталоне метра - материальном носители этой единице.

Д) Метр: В этом случае учащиеся испытали некоторые затруднения. В целом пришли к выводу, что выделено название. Можно было бы дать этой же единице длины и другое название. Но в математике из уважения к огромному вкладу в её развитие древнегреческих мыслителей принято многие основные понятия называть греческими словами («метрео» - по-гречески «измеряю»). (Аналогичную работу можно проделать при изучении единиц скорости, массы и т. д.)

Алгоритмизация обучения

Формированию информационной компетенции способствуют алгоритмизированные «памятки», которые развивают последовательность, обоснованность суждений и выводов. Алгоритмы это:

- инструктивные предписания (правила, инструкции, памятки),
определяющие четкую последовательность элементарных для данного
субъекта операций по решению учебной задачи и синтеза;

- система работы по строго определенным правилам, которая после
последовательного их выполнения приводит к решению поставленных задач.

Применение алгоритмов обеспечивает не только усвоение предметных знаний, но и организует процесс усвоения.

Следуя алгоритмическому предписанию, учащиеся выполняют не только исполнительские, но и ориентировочные действия, что обеспечивает формирование информационной компетенции.

Одним из этапов урока является изучение нового материала. Источником информации на уроке чаще всего служит учебник. Для облегчения работы можно предложить учащимся следующие алгоритмы.

Алгоритм работы с учебником.

I. Подготовительный этап.

1. Ознакомьтесь с содержанием параграфа:

·  изучите заголовки частей параграфа, что позволит получить общее представление об его содержании;

·  выделите главное для понимания содержания (из каких составных частей состоит параграф, в чем главная мысль каждой части);

·  просмотрите задания после параграфа, сопоставляя их с приведенными примерами.

2. Понимание и осмысление:

·  выделите в тексте главные мысли, ключевые понятия и термины, соотнесите их с ранее изученным материалом;

·  рассмотрите приведенные примеры, обращаясь к тексту, рисункам, старайтесь извлечь из них как можно больше сведений.

3. Запоминание:

·  выделите опорные ключевые слова, факты; запомните последовательность аргументации, изложения; мысленно дайте ответ на поставленные проблемы;

·  для лучшего запоминания учебного материала составьте его план или конспект, с приведением примеров;

·  воспроизведите мысленно ход изложения, и если не можете вспомнить какую-либо его часть, то еще раз прочитайте.

П. Завершающий этап.

Для закрепления и углубления знаний, самоконтроля выполните задания учителя или приведенные в конце параграфа.

Работая с текстом, нужно активно мыслить - задавать себе вопросы и искать на них ответы. .

Алгоритм составления конспекта.

1.  Ознакомьтесь с изучаемым материалом, выделите главное для понимания; подразделите текст на основные смысловые части, выводы.

2.  Составьте план-конспект: сформулируйте его пункты, подпункты, определите, что именно следует включить в план-конспект для раскрытия каждого из них.

3.  Наиболее существенные положения изучаемого материала (тезисы) последовательно и кратко изложите своими словами или приведите в виде цитат.

Включайте в конспект не только основные положения, но и обосновывающие их доводы, конкретные факты и примеры (без подробного описания).

Конспект можно составлять в сокращенной форме, делая лишь ссылки на страницы конспектируемой работы; применять условные обозначения.

Чтобы форма конспекта более наглядно отражала его содержание, располагайте абзацы «ступеньками», применяйте разнообразные способы выделения текста, используя карандаши, фломастеры, маркеры.

Одной из форм домашнего задания является подготовка доклада (сообщения). Доклад позволяет приобщить ученика к самостоятельной работе, умению искать, анализировать и отбирать необходимую информацию.

Алгоритм подготовки доклада.

Определите тему, сформулируйте ее основную мысль. Установите срок, к которому доклад должен быть приготовлен.

Подберите литературу по данному вопросу с помощью библио­графических пособий, библиографического каталога и других источников. Составьте план работы над докладом, получите консультацию учителя.

Внимательно прочитайте источник, в котором наиболее полно раскрыта тема вашего доклада. Составьте план доклада на основе этого источника.

Изучите дополнительную литературу, сделайте выписки (на листах или карточках), размещая их по разделам плана.

Не забывайте обращаться к справочной литературе и правильно оформляйте выписки. По вопросам, которые вас затрудняют, обращайтесь за консультацией к учителю.

Подготовьте окончательный текст доклада. Приступайте к оформлению выступления:

·  составьте подробный, развернутый план выступления, указывая в скобках фактический материал (порядковый номер выписки);

·  не забывайте ссылаться на используемые источники, тщательно аргументируйте свои выводы;

·  свое выступление завершите краткими выводами, которые должны оставлять у слушателей четкое представление о том, в чем вы хотели их убедить.

Несколько раз «проговорите» текст дома. Проконтролируйте отведенное вам время: если его окажется меньше, чем занимаемое выступление, сократите его, оставив только самое важное и интересное.

Подготовьте к своему выступлению наглядные пособия. Будьте готовы ответить на вопросы слушателей и защищать свою точку зрения.

Составление словаря терминов.

В ходе изучения материала появляется много новых терминов, значение которых объясняется с позиции физики. Но в других областях знаний имеет совсем другое значение. Например «тело» (материя и т. д.). В физике телом называют любой предмет, а в повседневной жизни мы говорим о теле человека, животного.

Поэтому можно предлагать учащимся домашнее задание на составление словарей, которые расширят знания учащихся. Для составления словарей учащиеся обратятся к справочной литературе, тем самым повысят уровень своей информационной компетенции.

Например, при изучении темы «Сила», одним из домашних заданий было найти в словарях понятие «сила» и проанализировать, какой из видов словарей дает более полную информацию об этом слове

Составление опорных конспектов по новому материалу. Этот прием уместен, если учитель сам применяет подобные конспекты и учит пользоваться ими учеников. Ученики могут объяснить друг другу свои опорные конспекты или обменяться опорными конспектами, для проговаривания темы по опорному конспекту соседа.

Школьные учебники содержат недостаточный дидактический материал для формирования информационной компетенции. Поэтому учитель, подготавливая учащихся к работе с информацией, обучая составлению словарей терминов, опорных конспектов, алгоритмов выполнения заданий, написанию докладов и их защите, поможет учащимся формировать информационную компетенцию.

Литература:

1.  Дахин и компетентность: сколько их у российского школьника? Народное образование №4 2004 г.

2.  Хуторской компетенции как компонент личностно-ориентированной парадигмы образования. Народное образование № 2 2003 г.

3.  Хуторской компетенции. Технология конструирования. Народное образование № 5 2003 г.

4.  Болотов модель: от идеи к образовательной программе. Педагогика №г.

5.  Концепция модернизации российского образования на период до 2010 г. Стратегия образования № 1 2002 г.

6.  Федеральный компонент государственного стандарта общего образования. Народное образование № 7 2004 г.

7.  Чикурова сформированность информационной компетенции. Школьные технологии № 3 2004 г.

, учитель физики МОУ СОШ № 69
ФОРМИРОВАНИЕ КЛЮЧЕВЫХ КОМПЕТЕНЦИЙ УЧАЩИХСЯ НА УРОКАХ ФИЗИКИ ПРИ РЕШЕНИИ ТВОРЧЕСКИХ ЗАДАЧ.

Компетенция – отчужденное, наперед заданное социальное требование (норма) к образовательной подготовке ученика, необходимой для его качественной продуктивной деятельности в определенной сфере.

Компетентность – владение, обладание учеником соответствующей компетенцией, включающее его личностное отношение к ней и предмету деятельности. Компетентность – уже состоявшееся личностное качество (совокупность качеств) ученика и минимальный опыт деятельности в заданной сфере.

Компетенции предлагаются ученикам для овладения, формирования у них соответствующих компетентностей.

Образовательные компетенции – совокупности взаимосвязанных смысловых ориентаций, знаний, умений, навыков и опыта деятельности ученика по отношению к определенному кругу объектов реальной действительности, необходимых для осуществления личностно и социально-значимой продуктивной деятельности.

Учебно-познавательная компетенция — это совокупность компетенций ученика в сфере самостоятельной познавательной деятельности, включающей элементы логической, методологической, общеучебной деятельности. Сюда входят способы организации целеполагания, планирования, анализа, рефлексии, самооценки. По отношению к изучаемым объектам ученик овладевает креативными навыками продуктивной деятельности: добыванием знаний непосредственно из реальности, владением приемами учебно-познавательных проблем, действий в нестандартных ситуациях. В рамках данной компетенции определяются требования функциональной грамотности: умение отличать факты от домыслов, владение измерительными навыками, использование вероятностных, статистических и иных методов познания.

На уроках физики как одно из средств развития компетенций учащихся выступает задача. Она является одним из важных факторов повышения познавательной активности учащихся. Задача требует от субъекта некоторого действия (идея, анализ условий реализации, получение продукта), которое не может возникнуть стихийно, вне определённых условий. Создание таких условий является одной из основных педагогических задач учителя.

Особую актуальность при оказании помощи учащимся приобретает разноуровневое использование задач, направленных на зону актуального и ближайшего развития школьников.

Теоретические и эмпирические исследования показывают, что учителю целесообразно иметь банк задач по отдельным курсам, темам и разделам учебного курса на основе уровней учебно-познавательного опыта школьников (низкий, средний, высокий), важнейшими компонентами которого являются знания, умения, навыки; познавательный интерес, умения саморегуляции и эмоциональная грамотность.

Процесс школьного обучения ограничен временными рамками, но «перешагнуть» за пределы отводимого для уроков времени можно с помощью учебных заданий на творческое применение знаний детьми, имеющими различный уровень учебно-познавательного опыта (задачи четвёртого уровня).

Задачи четвёртого уровня:

— составление и расшифровка анаграмм, криптограмм, ребусов;

— выстраивание последовательностей формул по правилу;

— выявление причинно-следственных связей при изменении численного значения физических постоянных;

— самостоятельная постановка задачи на предложенном стимульном материале;

— нахождение физических терминов в произвольно выбранном тексте;

— определение «областей жизни» и «сферы жизни» различных межпредметных понятий;

— отправление информации по зашифрованному в задаче адресу;

— написание сочинений;

— создание научно-фантастических рассказов;

— создание проектов;

— составление физических задач-шуток и т. д.

Решение таких задач развивает у детей познавательный интерес; умение ставить перед собой цель, определять план действий; уровень знаний; воображение, абстрактное мышление; анализ, синтез; авторство.

В процессе и в результате у школьника происходит обогащение учебно-познавательного опыта самостоятельного и под руководством учителя.

Использование учителем творческих заданий является одним из основных условий создания единого учебного пространства «ФИЗИКА» на уроке и вне его, а также формирования ключевых компетенций у учащихся.

, учитель физики МОУ СОШ № 154
ПРОЕКТНАЯ ДЕЯТЕЛЬНОСТЬ УЧАЩИХСЯ – ОДНО ИЗ УСЛОВИЙ РЕАЛИЗАЦИИ КОМПЕТЕНТНОСТНОГО ПОДХОДА ПРИ ОБУЧЕНИИ ФИЗИКЕ.

В 1928 году американский учёный Джон Дьюи, побывав в Советском Союзе написал книгу «Впечатления о революционном мире». В ней Дьюи высоко оценил философию школы: её общую направленность на ребёнка, ценности и принципы деятельности учителей и руководителей школы. Он был восхищён интеллектуальной смелостью учителей и руководителей школы, которые в те годы решали проблемы не стереотипными способами: для каждой проблемы искалось решение, соответствующее её ценностям. Учителя уже тогда считали, что педагогическая техника вторична, она – инструмент. Главное – это ценности и идеалы учителя и школы. Это ещё раз подтверждает, что для всякого реформирования важны исходные философские подходы.

В 20-е и в начале 30-х годов в российских школах широко использовался метод проектов для реализации выдвигаемых задач – развития ученика. Однако этот метод не давал возможности учащимся овладевать системой знаний в области конкретных учебных курсов, поэтому был изъят из школы, и вместе с этим резко снизилось внимание к основной философской идее образования того времени – направленность его на ребёнка.

В настоящее время эта идея вновь стала определяющей в деятельности российских школ, что объясняет интерес педагогов – практиков к технологии проектного обучения.

Чаще всего можно услышать не о проектном обучении, а о проектном методе. Этот метод чётко оформился в США к 1919 году. В России он получил широкое распространение после издания брошюры В. Х. Килпатрика «Метод проектов. Применение целевой установки в педагогическом процессе» (1925г).

В основе этой системы лежат идеи Дьюи, Лая, Торндайка и др. американских учёных. Главные их идеи состоят в следующем:

·  С большим увлечением выполняется ребёнком только та деятельность, которая им выбрана свободно самим.

·  Деятельность строится не в русле учебного предмета.

·  Опора на сиюминутные увлечения детей.

·  Истинное обучение никогда не бывает односторонним, важны и побочные сведения.

Исходный лозунг основателей проектного обучения – «Всё из жизни, всё для жизни».

В современных условиях можно говорить уже о создании основ проектного обучения. Следует отметить то, что переводить полностью весь образовательный процесс на проектное обучение нецелесообразно. Для современного этапа развития системы образования важно обогатить практику многообразием личностно – ориентированных технологий, одной из которых может стать технология проектного обучения.

Цель проектного обучения состоит в том, чтобы создать условия, при которых учащиеся:

·  Самостоятельно и охотно приобретают недостающие знания из разных источников.

·  Учатся пользоваться приобретёнными знаниями для решения познавательных и практических задач.

·  Приобретают коммуникативные умения, работая в различных группах.

·  Развивают у себя исследовательские умения (умения выявления проблем, сбора информации, наблюдения, проведения эксперимента, анализа, построения гипотез, обобщения).

·  Развивают системное мышление.

Исходные теоретические позиции проектного обучения:

·  В центре внимания – ученик, содействие развитию его творческих способностей.

·  Образовательный процесс строится не в логике учебного предмета, а в логике деятельности, имеющей личностный смысл для ученика, что повышает его мотивацию в учении.

·  Индивидуальный темп работы над проектом обеспечивает выход каждого ученика на свой уровень развития.

·  Комплексный подход к разработке учебных проектов способствует сбалансированному развитию основных физиологических и психических функций ученика.

·  Глубокое, осознанное усвоение базовых знаний обеспечивается за счёт универсального их использования в разных ситуациях.

Таким образом, суть проектного обучения состоит в том, что ученик в процессе работы над учебным проектом постигает реальные процессы, объекты и т. д. Оно предполагает проживание учеником конкретных ситуаций, приобщению его к проникновению вглубь явлений, процессов и конструированию новых объектов.

С целью выделения систем действий учителя и учащихся предварительно важно определить этапы разработки проекта. Можно выделить четыре основных этапа реализации учебного проекта: ценностно – ориентационный, конструктивный, оценочно – рефлексивный, презентативный.

На первом этапе происходит осознание школьниками мотивов и целей выполнения проекта, формируются представления о личностной значимости и практической важности этого проекта. Этот этап связан с выделением приоритетных компонентов проекта, определяющих его содержание и характер деятельности его участников.

На конструктивном этапе осуществляется планирование проектной деятельности, распределение обязанностей и видов работ между участниками коллектива, непосредственное выполнение проекта.

Оценочно – рефлексивный этап связан с самооценкой или взаимооценкой промежуточных и конечных результатов и коррекцией деятельности по выполнению проекта.

Презентативный этап проекта – это его презентация общественности и защита.

Одним из важнейших факторов успешной реализации профильного обучения, в частности развития преемственности школьного и вузовского образования в условиях использования методов учебных проектов, является роль проектов в формировании ключевых компетенций как наиболее значимого компонента учебных достижений и школьников, и студентов. Компетентностный подход отражает объективные потребности в усилении внимания к личностно – значимым и востребованным в практической деятельности результатам обучения в общем и профессиональном образовании.

Формирование и оценка овладения компетенциями неотделимы от конкретных условий и ситуаций, в которых они проявляются. При этом традиционные формы и методы обучения и в школе, и в вузе не всегда позволяют создавать подобные условия и ситуации.

Метод проектов является наиболее естественным способом создания в ходе обучения среды для формирования компетенций у обучаемых. При работе над проектом возникают предпосылки для эффективного освоения способов деятельности, составляющих самостоятельную познавательную, коммуникативную и информационную компетенции.

Сегодня школьная практика вновь обращается к методу проектов, но уже как к комплексному обучающему методу, который позволяет индивидуализировать учебный процесс, даёт ребёнку возможность проявить самостоятельность в планировании, организации и контроле своей деятельности. Модернизация образования должна быть направлена не только на глубокое усвоение теоретических основ предмета, но и на достижение методологической компетентности учащихся, т. е. приобретение ими универсальных умений и навыков исследовательской деятельности. Этому и служит проектный метод. В контексте физического образования проект – это самостоятельная творческая деятельность ученика по решению учебной проблемы, взятой из повседневной жизни. При работе над проектом формируются ещё и такие компетенции, как:

·  Коммуникативная – ученик стремится быть понятым.

·  Социальная – школьникам нравится работать в группе, занимая определённое положение в ней.

·  Предметная – проявление способностей в области физики.

Образовательная программа по физике «нашпигована высотами для покорения», при достижении которых учащиеся будут становиться более компетентными. Нужно лишь сформулировать такие темы проектов, работая над которыми школьники ощутили бы потребность и необходимость в получении систематических научных знаний. Начинать лучше с микропроектов. Например, в 10 кл при изучении электродинамики можно предложить следующий микропроект: определить схему включения четырёх одинаковых резисторов в чёрном ящике, если известно сопротивление каждого из них и можно измерить эквивалентное сопротивление схемы.

Выполнение микропроектов служит этапом подготовки к более серьёзной работе. В качестве примера можно привести долгосрочный проект «Исследование движения тела переменной массы», в процессе которого группе учеников приходится выполнять проектную деятельность – конструировать приборы и установки для экспериментального доказательства законов движения тел переменной массы: уравнение Мещерского и формулу Циолковского.

Проектный метод обучения позволяет учащимся глубже осознать теоретические основы курса и его практическое значение, так как не решаемые, на первый взгляд, проблемы с помощью законов физики становятся достаточно простыми.

СЕКЦИЯ № 10
«Информационно-коммуникационные технологии как средство реализации компетентностного подхода»

, учитель информатики МОУ СОШ № 000
РЕАЛИЗАЦИЯ КОМПЕТЕНТНОСТНОГО ПОДХОДА В ОБРАЗОВАНИИ ЧЕРЕЗ ОРГАНИЗАЦИЮ ПРОЕКТНОЙ ДЕЯТЕЛЬНОСТИ ОБУЧАЮЩИХСЯ НА УРОКАХ ИНФОРМАТИКИ.

С позиций компетентностного подхода основным непосредственным результатом в образовательной деятельности современного общества становится формирование ключевых компетенций обучающихся (об этом мы говорили на семинаре учителей информатики Калининского района в апреле 2006г.). Под ключевыми компетенциями понимается способность учащихся самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем. Педагоги во всем мире давно уже осознали, что жесткое регламентирование интеллектуальной деятельности, абсолютная заданность развития, грозят стать тормозящим фактором, ограничивающим инициативу и творческие возможности обучающихся. В программах Московского института образовательных программ несколько лет назад было зафиксировано: в условиях информационного взрыва ориентация содержания на еще недостигнутый уровень развития науки и техники возможна только при условии формирования установки на развитие мышления.

Мышление, способное усвоить знания будущего, называют проектным.

Именно в силу того, что проектное мышление включает в себя фундаментальные методы познания, необходимые во всякой созидательной деятельности, воспитание его видится специалистам необходимой составной частью системы общего образования, та как тесно связано с формированием ключевых компетенций у учащихся.

По к ключевым образовательным компетенциям относятся:

- Ценностно-смысловая компетенция. Это компетенция в сфере мировоззрения, связанная с ценностными ориентирами ученика, его способностью видеть и понимать окружающий мир, ориентироваться в нем, осознавать свою роль и предназначение, уметь выбирать целевые и смысловые установки для своих действий и поступков, принимать решения. Данная компетенция обеспечивает механизм самоопределения ученика в ситуациях учебной и иной деятельности. От нее зависит индивидуальная образовательная траектория ученика и программа его жизнедеятельности в целом.

- 06щекультурная компетенция. Познание и опыт деятельности в области национальной и общечеловеческой культуры; духовно-нравственные основы жизни человека и человечества, отдельных народов; культурологические основы семейных, социальных, общественных явлений и традиций; роль науки и религии в жизни человека; компетенции в бытовой и культурно-досуговой сфере, например, владение эффективными способами организации свободного времени. Сюда же относится опыт освоения учеником научной картины мира, расширяющейся до культурологического и всечеловеческого понимания мира.

- Уче6но-познавательная компетенция. Это совокупность компетенций ученика в сфере самостоятельной познавательной деятельности, включающей элементы логической, методологической, общеучебной деятельности. Сюда входят способы организации целеполагания, планирования, анализа, рефлексии, самооценки. По отношению к изучаемым объектам ученик овладевает креативными навыками продуктивной деятельности: добыванием знаний непосредственно из реальности, владением приемами учебно-познавательных проблем, действий в нестандартных ситуациях. В рамках данной компетенции определяются требования функциональной грамотности: умение отличать факты от домыслов, владение измерительными навыками, использование вероятностных, статистических и иных методов познания.

- Информационная компетенция. Навыки деятельности по отношению к информации в учебных предметах и образовательных областях, а также в окружающем мире. Владение современными средствами информации (телевизор, магнитофон, телефон, факс, компьютер, принтер, модем, копир и т. п.) и информационными технологиями (аудиовидеозапись, электронная почта, СМИ, Интернет). Поиск, анализ и отбор необходимой информации, ее преобразование, сохранение и передача.

- Коммуникативная компетенция. Знание языков, способов взаимодействия с окружающими и удаленными людьми и событиями; навыки работы в группе, коллективе, владение различными социальными ролями. Ученик должен уметь представить себя, написать письмо, анкету, заявление, задать вопрос, вести дискуссию и др. Для освоения данной компетенции в учебном процессе фиксируется необходимое и достаточное количество реальных объектов коммуникации и способов работы с ними для ученика каждой ступени обучения в рамках каждого изучаемого предмета или образовательной области.

- Социально-трудовая компетенция. Выполнение роли гражданина, наблюдателя, избирателя, представителя, потребителя, покупателя, клиента, производителя, члена семьи). Права и обязанности в вопросах экономики и права, в области профессионального самоопределения. В данную компетенцию входят, например, умения анализировать ситуацию на рынке труда, действовать в соответствии с личной и общественной выгодой, владеть этикой трудовых и гражданских взаимоотношений.

- Компетенция личностного самосовершенствования направлена на освоение способов физического, духовного и интеллектуального саморазвития, эмоциональной саморегуляции и самоподдержки. Ученик овладевает способами деятельности в собственных интересах и возможностях, что выражаются в его непрерывном самопознании, развитии необходимых современному человеку личностных качеств, формировании психологической грамотности, культуры мышления и поведения. К данной компетенции относятся правила личной гигиены, забота о собственном здоровье, половая грамотность, внутренняя экологическая культура, способы безопасной жизнедеятельности.

Формирование всех этих ключевых образовательных компетенций в большей степени проявляется при организации проектной деятельности учащихся. Проектная деятельность учащихся выступает как процесс связывания ценностного и деятельностного компонентов субъекта проектирования, происходящий в информационно-образовательном пространстве, влияющем на развитие личности.

В Российской педагогической энциклопедии Метод проектов определяется как «система взглядов, при которой учащиеся приобретают знания в процессе планирования и выполнения постепенно усложняющихся практических заданий-проектов».

В основе использования Метода проектов лежат три базовых принципа:

1 – свобода ребенка;

2 – взаимодействие его с группой детей;

3 – гибкое распределение учебного времени.

Положительными сторонами Метода проектов являются: направленность на индивидуализацию обучения, активизацию учения, стимулирование инициативы и роста творческих возможностей.

Проектная форма организации деятельности школьника должна включать в себя две основные составляющие:

1 – наличие большой доли исходной аналитической информации;

2 – реализация собственной модели исходной информационной задачи.

Структуру проектной деятельности учащихся можно представить в виде таблицы:

Структура проекта

1.  Формулировка темы.

2.  Постановка проблемы.

3.  Анализ исходной ситуации.

4.  Задачи, решаемые в ходе выполнения проекта: а) организационные; б) учебные; в) мотивационные.

5.  Этапы реализации проекта.

6.  Возможные критерии оценивания уровня реализации проекта.

В качестве итогового мероприятия проводится рефлексия для определения уровня осознанности проделанной работы, и в зависимости от уровня и масштаба проведенных работ организуются либо конференции, либо ученические чтения.

Методика организации проектной деятельности школьников

На основе научной, научно-методической литературы были выделены основные методические подходы для организации проектной деятельности:

1. Обучение с опорой на систему базовых понятий

Система базовых понятий «информация - система - структура - сеть» состоит из трех понятий, которые отнесены к первичным, т. е. необъяснимым понятиям, которые мы должны принять как аксиому (, 1982). Как доказывают психологические исследования, при отсутствии систематической работы с понятиями, в сознании человека складывается понятие на уровне бытового представления (понятие-комплекс), т. е. понятие, не имеющее научного содержания (, 1936). Для конкретных понятий это несущественно, для абстрактных понятий - это катастрофично.

«Вещи (объекты) следует рассматривать как некие целостные совокупности (или, как мы сейчас говорим, системы), состоящие из более мягких частей (элементов); что элементы находятся в определенных взаимных зависимостях (отношениях) и обладают теми или иными качествами (свойствами, характеристиками); что согласованное взаимодействие частей обусловлено обменом сигналами (информацией), в результате чего вещь остается равной самой себе (сохраняет свою структуру) и т. д.» (, 1988).

Методика включает в себя систему определений понятия информации, доступную для восприятия и понимания учащихся среднего звена общеобразовательной школы. Понятие информации вводится «методом последовательных приближений» - введение понятия осуществляется «по спирали»: от целенаправленного выявления «житейских» представлений и «первоначальных понятий», в которых чувственный опыт играет определяющую роль, до формирования «псевдопонятий» и, наконец, научных понятий (, , и др.). Понятию информации уделяется определенное внимание на каждом уроке в контексте изучения очередной темы про граммы курса информатики.

Понятия «система» и «структура» также вводятся последовательно, из урока в урок, при решении информационных задач и при объяснении каждой темы. Все явления, процессы и объекты рассматриваются через призму данных понятий. Конкретизация понятий «система» и «структура» происходит при объяснении темы «Телекоммуникации», с вводом понятия «сеть».

2. Формирование индивидуального образовательного маршрута

Существуют два вида технологий, позволяющих реализовать идею использования индивидуального образовательного маршрута. Первый вид - это дифференциация обучения, другой - эвристическое обучение. При организации проектной деятельности наиболее эффективным средством выступает методология эвристического обучения (, 1998), в основе которой лежит идея самореализации личностного потенциала каждого учащегося. В качестве ориентиров используются конкретные личностные способности учащихся.

3. Единый перечень проектов для всего школьного курса информатики

Перечень тем проектов являются открытыми и не зависят от возраста учащихся и года обучения информатике. Единственным критерием выбора темы является личная заинтересованность учащегося в работе над данным проектом.

4. Итоговое оценивание учащихся производится на материале проектной работы. Критериями оценивания проекта выступают:

1) обоснованность актуальности темы проекта и предлагаемых решений;

2) объем, полнота разработок, самостоятельность, законченность;

3) уровень творчества, оригинальность раскрытия темы;

4) дизайн, стиль, соответствие стандартным требования к веб-ресурсам, структура текста, качество схем, рисунков, анимации;

5) качество доклада;

6) проявление глубины и широты заданий по излагаемой теме.

5. Учебный материал носит общетеоретический характер с демонстрацией основных технологических принципов работы ПО

Реализуется системный подход, когда учитель, вместо конкретных пояснений о работе с программным продуктом, дает общие принципы работы с тем или иным ПО. При таком подходе не возникает сложности усвоения других аналогичных программных средств.

Учащимся в процессе обучения информатике выдается проектное задание: построить конкретную модель системно-информационной картины мира. Структурная сложность построенной модели служит также критерием установления уровня систематизации знаний учащихся.

, заведующий медиа - классом, преподаватель-организатор ОБЖ МОУ СОШ № 000
ОРГАНИЗАЦИЯ РАБОТЫ МЕДИА-КЛАССА ПО ФОРМИРОВАНИЮ ИКТ КОМПЕТЕНТНОСТИ УЧАСТНИКОВ ОБРАЗОВАТЕЛЬНОГО ПРОЦЕССА.

(Общая) информационно-коммуникативная компетентность (ИК - компетентность) – умение решать распространенные информационные задачи, используя современные общедоступные информационные ресурсы (инструменты и источники)

Профессиональная ИК – компетентность – умение решать информационные задачи профессиональной области, используя современные общедоступные в профессиональной области информационные ресурсы (инструменты и источники)

Из за большого объема эта статья размещена на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12