Выбор способа определения средней величины зависит от исходных данных.

Перечисленные средние объединяются в общей формуле средней степенной (при различной величине k):

, (10)

где – средняя величина исследуемого явления;

– i-й вариант осредняемого признака ();

– вес i - го вырианта.

Помимо степенных средних в статистической практике также используются средние структурные, среди которых наиболее рас­пространены мода и медиана. При осреднении уровней динамических рядов применяются раз­личные виды средней хронологической.

3.3. Средняя арифметическая и ее свойства

Наиболее распространенным видом средних величин являет­ся средняя арифметическая, которая в зави­симости от характера имеющихся данных может быть простой или взвешенной.

Средняя арифметическая применяется, если известны значения признака xi и число единиц fi, обладающих этим признаком.

1. Если для каждого xi известна только одна единица, обладающая этим признаком, применяется средняя арифметическая простая (невзвешенная). Эта форма средней используется в тех случаях, когда расчет осуществляется по несгруппированным данным.

, (11)

где n – число единиц изучаемой совокупности

Пример. Определить среднюю зарплату рабочих бригады по следующим данным:

Рабочий бригады получает в среднем 550 руб.

2. Если в исходных данных известны отдельные значения признака xi и для каждого своя численность единиц fi, применяется средняя арифметическая взвешенная.

,

Пример. Определить средний балл студентов по теории статистики:

На экзамене по теории статистики студенты получили в среднем 3,5 балла.

При нахождении средней по интервальному вариационному ряду используется следующий порядок расчета:

1.  Закрываются открытые интервалы, приняв их равными ближайшим закрытым.

2.  От интервального ряда переходим к дискретному – в каждом интервале находится середина x=(xmax+xmin)/2, где xmax – верхняя граница интервала, xmin – нижняя.

3.  Расчет производится по средней арифметической взвешенной.

Пример. Определить средний возраст студентов в группе по данным таблицы:

Средний возраст студента в группе составляет 18,8 года.

В отд. случаях веса могут быть представлены не абсолютными величинами, а относительными (в % или долях единицы). В этом случае получаем формулу:

, (12)

Рассмотрим расчет средней способом моментов:

1.  Из всех вариантов xi выбирается какое-то одно за базу отсчета, которое обозначается xо. Может быть выбрано любое xi, но для упрощения расчетов лучше брать xi, имеющее наибольшую частоту fi.

2.  От фактических вариантов xi переходим к условным x i 1, которые вычисляются по формуле:

,

где h – ширина равного интервала.

3. Расчет средней по формуле:

– (начальный) момент 1-го порядка.

Пример. Имеется распределение предприятий по стоимости основных фондов (ОФ).

Определить средний размер стоимости ОФ данных предприятий:

1)  по средней арифметической взвешенной;

2)  способом моментов.

1)

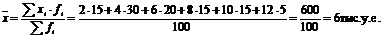
2) основные этапы расчета средней способом моментов представлены в графах 4–6.

Средний размер стоимости ОФ рассматриваемых предприятий составил 6 тыс. у. е.

Свойства средней арифметической.

1. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:

Математическое доказательство:

2. Если все усредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину:

3. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз:

4. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится:

Исходя из данного свойства можно заключить, что в случае равенства всех весов расчеты по средней арифметической взвешенной и средней арифметической простой приведут к одному и тому же результату.

3.4. Другие виды средних

При расчете статистических показателей помимо средней арифметической могут использоваться и другие виды средних. Однако в каждом конкретном случае в зависимости от характера имеющихся данных существует только одно истинное среднее значение показателя, являющееся следствием реализации его исходного соотношения.

1. Средняя гармоническая

Средняя гармоническая взвешенная

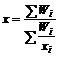, (13)

где Wi = xi fi – объем осредняемого признака для определенного числа единиц совокупности.

Например, если усредняется зарплата, то W – зарплата всех рабочих, т. е. фонд заработной платы; если определяем средние затраты времени на изготовление одного изделия, то W – затраты времени на изготовление всех изделий.

Пример. Имеются следующие данные:

Определить среднюю зарплату всех цехов.

В исходных данных известны значения усредняемого признака xi и объем усредняемого признака Wi для каждого значения xi ® применяем среднюю гармоническую взвешенную.

Рабочие 3-х цехов получают в среднем 650 рублей.

2. Средняя гармоническая простая

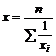, (14)

Средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения Wi для единиц совокупности равны.

3. Средняя геометрическая. Наиболее широко применение этот вид средней получил в анализе динамики для определения среднего темпа роста (подробнее см. гл.7).

4. Средняя квадратическая. Наиболее широко данный вид средней используется при расчете показателей вариации (подробнее см. гл. 4).

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15