При таком обозначении границ может возникнуть вопрос, в ка­кую группу включать единицы объекта, значения признака у ко­торых совпадают с границами интервалов. Например, во вторую или третью группу должно войти предприятие со стоимостью фондов 790 млн руб. Если нижняя граница формируется по прин­ципу «включительно», а верхняя – по принципу «исключительно», то предприятие должно быть отнесено к третьей группе, в про­тивном случае – ко второй. Для того чтобы правильно отнести к той или иной группе единицу объекта, у которой значение при­знака совпадает с границами интервалов, можно использовать открытые интервалы.

Если в основании группировки лежит дискретный признак, то нижняя граница 1-го интервала равна верхней границе 1–1-го ин­тервала, увеличенной на 1.

Например, пусть совокупность состоит из 80 предприятий и ее надо разделить на группы по численности занятых. Минимальное и максимальное значения группировочного признака соответствен­но равны 290 и 2040 человек. В этом случае возможны следую­щие варианты построения групп (табл. 4).

Т а б л и ц а 4

Варианты построения групп

Неравные интервалы применяются в статистике, когда значе­ния признака варьируют неравномерно и в значительных разме­рах, что характерно для большинства социально-экономических явлений, особенно при анализе макроэкономических показателей.

После определения группировочного признака и границ групп строится ряд распределения.

Статистический ряд распределения – это упорядоченное рас­пределение единиц совокупности на группы по определенному ва­рьирующему признаку.

Ряд распределения принято оформ­лять в виде таблиц. В зависимости от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения.

Атрибутивными называют ряды распределения, построенные по качественным признакам.

Вариационными называют ряды распределения, построенные по количественному признаку. Любой вариационный ряд состоит из двух элементов: вариантов и частот. Вариантами считаются отдельные значения признака, которые он принимает в вариаци­онном ряду, т. е. конкретное значение варьирующего признака. Частоты – это численности отдельных вариантов или каждой груп­пы вариационного ряда, т. е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот определяет численность всей совокупности, ее объем. Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100 %.

В зависимости от характера вариации признака различают дис­кретные и интервальные вариационные ряды. Примером дискретного ва­риационного ряда является распределение семей по числу ком­нат в отдельных квартирах, приведенное в табл. 5.

Т а б л и ц а 5

Распределение семей по числу занимаемых комнат в отдельных квартирах в 1989 г. в РФ

В первой колонке таблицы представлены варианты дискретно­го вариационного ряда, во второй – помещены частоты вариаци­онного ряда, а в третьей – показаны частости.

В случае непрерывной вариации величина признака у единиц совокупности может принимать в определенных пределах любые значения, отличающиеся друг от друга на сколько угодно малую величину. Построение интервальных вариационных рядов целесообразно, прежде всего, при непрерывной вариации признака, а также, если дискретная вариация проявляется в широких преде­лах, т. е. число вариантов дискретного признака достаточно вели­ко.

Ряд распределения представляет собой простейшую группиров­ку, в которой каждая выделяемая группа характеризуется одним показателем – численностью единиц объекта, попавших в каждую группу. Построение рядов распределения является составной частью сводной обработки данных, при которой каждая группа еди­ниц характеризуется многими показателями. Поэтому важным мо­ментом в построении группировки является перечень тех показа­телей, которыми будет характеризоваться каждая группа.

2.2. Статистические таблицы

Результаты сводки и группировки материалов статистического наблюдения, как правило, излагаются в виде таблиц. Таблица является наиболее рациональной, наглядной и компак­тной формой представления статистического материала. Однако не всякая таблица является статистической. Таблица умножения, опросный лист социологического обследования и т. д. могут носить табличную форму, но еще не являются статистичес­кими таблицами.

Статистическую таблицу от других табличных форм от­личает следующее:

• она должна содержать результаты подсчета эмпирических дан­ных;

• она является итогом сводки первоначальной информации.

Статистической называется таблица, которая содержит сводную числовую характеристику исследуемой совокуп­ности по одному или нескольким существенным признакам.

Основные элементы статистической таблицы, представленные на рис.1, составляют ее основу.

Т а б л и ц а

Название таблицы*

(общий заголовок)

* Примечания к таблице

Рис. 1. Основные элементы статистической таблицы

Табличная форма расположения числовой информации – это такая, при которой число располагается на пересечении четко сформулированного заголовка по вертикальному столбцу, называ­емому графой, и сформулированного названия по соответствую­щей горизонтальной полосе – строке.

Таблица представляет собой пересече­ние граф и строк, которые формируют ее остов (основу). Каждое пересе­чение образует клетку таблицы. Размер таблицы определяется про­изведением числа строк на число граф.

Статистическая таблица содержит три вида заголовков: общий, верхние и боковые. Общий заголовок отражает содержание всей таблицы (к какому месту и времени она относится), располагает­ся над ее макетом по центру и является внешним заголовком. Вер­хние заголовки характеризуют содержание граф (заголовки сказу­емого), а боковые (заголовки подлежащего) – строк. Они являют­ся внутренними заголовками.

Остов таблицы, заполненный заголовками, образует ее макет. Если на пересечении граф и строк записать цифры, то получает­ся полная статистическая таблица.

Цифровой материал может быть представлен абсолютными (численность населения страны), относительными (индексы цен на продовольственные товары) и средними (среднемесячный доход служащего) величинами.

В случае необходимости таблицы могут сопровождаться приме­чанием, используемым с целью пояснения заголовков, методики расчета некоторых показателей, источников информации и т. д.

Подлежащим статистической таблицы называется объект, ха­рак-теризующийся цифрами. Это могут быть одна или несколько совокупностей, отдельные единицы совокупностей (фирмы, объе­динения) в порядке их перечня или сгруппированные по каким-либо признакам. Обычно подлежащее таблицы дается в левой части, в наименовании строк.

Сказуемое статистической таблицы образует система показа­телей, которыми характеризуется объект изучения, т. е. подлежа­щее таблицы. Сказуемое формирует верхние заголовки и состав­ляет содержание граф с логически последовательным расположе­нием показателей слева направо.

Расположение подлежащего и сказуемого может меняться ме­стами, что зависит от достижения каждым исследователем в от­дельности наиболее полного и лучшего способа прочтения и ана­лиза исходной информации об исследуемой совокупности.

В зависимости от структуры подлежащего и группировки в нем единиц различают статистические таблицы:

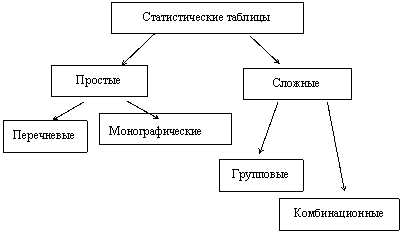В простой таблице в подлежащем дается простой перечень каких-либо объектов или территориальных единиц, т. е. в под­лежащем нет группировки единиц совокупности.

Простые таб­лицы бывают монографические и перечневые. Монографичес­кие таблицы характеризуют не всю совокупность единиц изуча­емого объекта, а только одну какую-либо группу из него, выде­ленную по определенному, заранее сформулированному признаку (табл. 6).

Т а б л и ц а 6

Характеристика успеваемости студентов 3-го года обучения

университета в 2000 г.

Перестроив подлежащее табл. 6, т. е. показав каждую единицу совокупности, получа­ем перечневую таблицу (табл. 7).

Т а б л и ц а 7

Характеристика успеваемости студентов 3-го года обучения

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15