При расчете относительного показателя абсолютный показа­тель, находящийся в числителе получаемого отношения, называ­ется текущим или сравниваемым. Показатель, с которым про­изводится сравнение и который находится в знаменателе, называется основанием или базой сравнения.

Таким образом, рас­считываемый относительный показатель указывает, во сколько раз сравниваемый абсолютный показатель больше базисного, или какую он составляет от него долю, или сколько единиц первого приходится на 1, 100, 1000 и т. д. единиц второго.

Относительные показатели могут выражаться в коэффициентах, процентах, промилле, продецимилле или быть именованными чис­лами. Если база сравнения принимается за 1, то относительный показатель выражается в коэффициентах, если база принимает­ся за 100, 1000 или 10 000, то относительный показатель соответ­ственно выражается в процентах (%), промилле и продеци­милле.

Проценты, как правило, используются в тех случаях, когда срав­ниваемый абсолютный показатель превосходит базисный не бо­лее чем в 2–3 раза. Проценты же свыше 200–300 обычно заменя­ются кратным отношением, коэффициентом. Так, вместо 480 % го­ворят, что сравниваемый показатель превосходит базисный в 4,8 раза.

Относительный показатель, полученный в результате соотнесе­ния разноименных абсолютных показателей, в большинстве слу­чаев должен быть именованным. Его наименование представля­ет собой сочетание наименований сравниваемого и базисного по­казателей (например, производство какой-либо продукции в соот­ветствующих единицах измерения в расчете на душу населения).

Все используемые на практике относительные статистичес­кие показатели можно подразделить на следующие виды:

-  динамики;

-  плана;

-  реализации плана;

-  структуры;

-  координации;

-  интенсивности и уровня экономического развития;

-  сравнения.

Относительный показатель динамики (ОПД) представляет собой отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент време­ни) к уровню этого же процесса или явления в прошлом:

, (3)

Рассчитанная величина показывает, во сколько раз текущий уровень превышает предшествующий (базисный) или какую долю от последнего составляет. Если данный показатель выражен кратным отношением, он называется коэффициентом роста, при домножении этого коэффициента на 100 % получают темп роста.

Все субъекты финансово-хозяйственной сферы, начиная от не­больших семейных предприятий и заканчивая крупными концер­нами, в той или иной степени осуществляют перспективное пла­нирование своей деятельности, а также сравнивают реально достигнутые результаты с ранее намеченными. Для этой цели ис­пользуются относительные показатели плана (ОПП) и реали­зации плана (ОПРП):

, (4)

, (5)

Предположим, оборот коммерческой фирмы в 2000 г. составил 1,8 млн. руб. Исходя из проведенного анализа складывающихся на рынке тенденций, руководство фирмы считает реальным в сле­дующем году довести оборот до 2,5 млн. руб. В этом случае от­носительный показатель плана, представляющий собой отноше­ние планируемой величины к фактически достигнутой, составит 139 % (2,5/1,8 • 100 %). Предположим теперь, что фактический обо­рот фирмы за 2001 г. составил 2,2 млн. руб. Тогда относительный показатель реализации плана, определяемый как отношение фак­тически достигнутой величины к ранее планированной, составит 88 % (2,2/2,5 • 100 %).

Между относительными показателями плана, реализации пла­на и динамики существует следующая взаимосвязь:

, (6)

В нашем примере: или ОПД = 2,2/1,8 = 1,22

Относительный показатель структуры (ОПС) представляет собой соотношение структурных частей изучаемого объекта и их целого:

(7)

Относительный показатель структуры выражается в долях еди­ницы или в процентах. Рассчитанные величины (di,), соответственно называемые долями или удельными весами, показывают, какой долей обладает или какой удельный вес имеет i-я часть в общем итоге. Сумма всех удельных весов всегда должна бы строго равна 100 %.

Относительный показатель интенсивности (ОПИ) характе­ризует степень распространения изучаемого процесса или явле­ния в присущей ему среде:

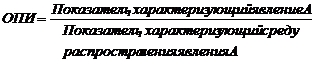, (8)

Этот показатель исчисляется, когда абсолютная величина ока­зывается недостаточной для формулировки обоснованных выво­дов о масштабах явления, его размерах, насыщенности, плотнос­ти распространения. Как и в предшествующем случае, он может выражаться в процентах, промилле или быть именованной вели­чиной. Например, для определения уровня рождаемости, измеря­емого в промиллях, рассчитывается число родившихся на 1000 человек на­селения, для определения плотности населения рассчитывается число людей, приходящихся на 1 км2 территории.

Расчет относительных показателей интенсивности в ряде слу­чаев связан с проблемой выбора наиболее обоснованной, соот­ветствующей данному процессу или явлению базы сравнения.

Разновидностью относительных показателей интенсивности являются относительные показатели уровня экономического развития, характеризующие производство продукции в расчете на душу населения и играющие важную роль в оценке развития эко­номики государства.

Относительный показатель сравнения (ОПСр) представля­ет собой соотношение одноименных абсолютных показателей, ха­рактеризующих разные объекты (предприятия, фирмы, районы, области, страны и т. п.):

, (9)

3.2. Сущность и значение средних показателей

Наиболее распространенной формой статистических показате­лей, используемой в социально-экономических исследованиях, яв­ляется средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.

Показатель в форме средней величины выражает типичные черты и дает обобщенную характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности. Широкое применение сред­них показателей объясняется тем, что они имеют ряд положительных свойств делающих их незаменимыми в анализе явлений и процессов об­щественной жизни.

Проиллюстрируем значение средних показателей на следующем примере. Одной из задач органов государственной статистики яв­ляется характеристика уровня жизни населения в целом и, в част­ности, уровня его доходов в разрезе различных социальных групп. Очевидно, что данный объект включает столь большое число еди­ниц, что сравнение индивидуальных доходов каждой семьи рабо­чего, служащего, предпринимателя, студента и т. д. является аб­солютно невозможным. Не представляет особого интереса и срав­нение суммарных доходов отдельных социальных групп, так как эти группы существенно различаются по численности (например, численность рабочих и численность людей, занятых в сфере пред­принимательства). В данном случае мы можем использовать лишь средние показатели, а именно среднюю величину доходов в рас­чете на одного человека или на одну семью по каждой социаль­ной группе.

Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупнос­ти могут колебаться в ту или иную сторону под влиянием множе­ства факторов, среди которых могут быть как основные, так и слу­чайные. Например, доходы такой социальной группы, как студен­ты государственных вузов, в целом определяются действующим положением о начислении стипендии. В то же время доходы от­дельно взятого студента могут быть и очень большими (предпо­ложим, вследствие занятия каким-либо бизнесом в свободное от учебы время или хорошо оплачиваемых сезонных работ), и совсем отсутствовать (например, при нахождении в академическом отпус­ке). Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц сово­купности, обусловленные действием случайных факторов, и учи­тываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и аб­страгироваться от индивидуальных особенностей, присущих отдельным единицам. Возможно, что ни один студент в границах исследуемой совокупности не имеет с точностью до рубля такого.

Типичность средней непосредственным образом связана с од­нородностью статистической совокупности. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. Так, в при­веденном примере, если мы рассчитаем средний уровень доходов служащих, то получим фиктивную среднюю. Это объясняется тем, что используемая для расчета средней совокупность, включающая служащих государственных, совместных, арендных, акционерных предприятий, а также органов государственного управления, сфе­ры науки, культуры, образования и т. п., является крайне неодно­родной. В этом и подобных случаях метод средних используется в сочетании с методом группировок: если совокупность неоднород­на – общие средние должны быть заменены или дополнены груп­повыми средними, т. е. средними, рассчитанными по качественно однородным группам.

В статистике применяются следующие формы средней величины:

1) средняя арифметическая;

2) средняя гармоническая;

3) средняя квадратическая, кубическая и т. д.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15